Department of Mathematical Sciences, Clemson University, Clemson, SC 29634-1907, USA.
Received: 22/08/2015 Accepted: 13/10/2015 Published: 23/10/2015
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
First hitting time models are a technique of modeling a stochastic process as it approaches or avoids a boundary, also known as a threshold. The process itself may be unobservable, making this a difficult problem. Regression techniques, however, can be employed to model the data as it compares to the threshold, creating a class of first hitting time models called threshold regression models. Survival data, measuring the amount of time before an event occurs, is widely used in modeling medical and manufacturing data. To analyze and model the data at hand, one commonly used method is the proportional hazards model, but this requires a strong proportional hazards assumption, one that is often lacking in practice. In place of the proportional hazards model, first hitting time models can be employed. First hitting time models do not require such strong assumptions and can be extended to become threshold regression models. Threshold regression has many advantages over the proportional hazards model, including its flexibility in both its assumptions and utilization and its application to stochastic processes so often evident in measuring survival. This paper describes the process of threshold regression modeling and compares its results and utility against that of the proportional hazards model. This approach is presented in a some interesting applications.
Threshold regression; First hitting time models; Exact solution; Markov decomposition.
First hitting time models are a technique of modeling a stochastic process as it approaches or avoids a boundary, also known as a threshold. The process itself may be unobservable, making this a difficult problem. Regression techniques, however, can be employed to model the data as it compares to the threshold, creating a class of first hitting time models called threshold regression models. Survival data, measuring the amount of time before an event occurs, is widely used in modeling medical and manufacturing data. To analyze and model the data at hand, one commonly used method is the proportional hazards model, but this requires a strong proportional hazards assumption, one that is often lacking in practice. In place of the proportional hazards model, first hitting time models can be employed. First hitting time models do not require such strong assumptions and can be extended to become threshold regression models. Threshold regression has many advantages over the proportional hazards model, including its flexibility in both its assumptions and utilization and its application to stochastic processes so often evident in measuring survival. This paper describes the process of threshold regression modeling and compares its results and utility against that of the proportional hazards model.
Section 2 gives a brief overview of survival data and some important vocabulary associated with the area of study. Section 3 outlines the basics of the proportional hazards model and describes its advantages and shortcomings. Section 4 describes the first hitting time model and its application to longitudinal and other types of data. Section 5 considers the specific case of the threshold regression model and the different ways it can be utilized for different data. Section 6 provides examples of threshold regression and compares the results to the proportional hazards model. Finally, Section 7 provides a conclusion and a short discussion of the results.
Survival data, or time-to-event data, measures the amount of time before some event, usually referred to as a failure, occurs. Survival analysis, encompassing the various methods used to model and analyze survival data, is useful in a multitude of areas, especially in modeling medical and engineering data.
A failure can be any event of interest to the researcher, in many cases referring to a biological death or mechanical breakdown. In medical applications, a failure is usually the death of a patient from a disease or injury of interest, the time of diagnosis or the time when a patient is cured (i.e., the event of interest is full recovery from an illness). In engineering, failure most commonly refers to a piece of machinery no longer being able to adequately perform its function.
In most studies, a failure does not occur for one or more subjects. For example, a patient may remain in good health or a machine may continue to function properly at the end of the study. In these cases, the subject’s status is measured for the final time at a censoring time, usually when the study is completed, though individual subjects can have personal censoring times as well. These censored observations must be considered separately from those that meet the failure criteria, as will be reflected in the partial likelihood function for the process, as discussed later.
Observable data, that which can be measured and recorded, are by far the most convenient to implement. For many studies involving human subjects, however, measurements may be missing or impossible to determine. Unobservable, or latent, data are the result of conditions that are too complex, subtle or difficult to record [1]. In these cases, other, observable variables must be used to obtain as much relevant information as possible about the missing measurements.
Proportional hazards models are often used for prediction in survival analysis. These models require an appropriate hazard function as well as a strong proportional hazards assumption. This assumption states that the covariates are multiplicatively related to the hazard function [2]. The hazard function, h(t) , gives the instantaneous rate of failure as [3]:
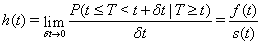
where t is the time in question, T is the failure time, f (t) is the failure density function and s(t) is the survival function, i.e., the probability of surviving until at least time t .
The hazard functions in proportional hazards models are proportional to a baseline hazard,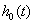
which yields a useful property. Suppose we have subjects with covariate values 
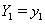and 
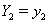. Then [3]:
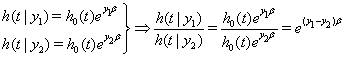
Therefore the hazard ratio at any time t does not depend on t [2]. Under the proportional hazards assumption, the survival funcitons for observations with different covariate values do not intersect [3].
Due to the strong nature of this proportional hazards assumption, though, many proportional hazards models fail. Nonproportional hazards can be caused by unexplained similarities in the risk or covariates that change over time within subjects [2]. Using proportional hazards also limits the outcome of the model. Most notably, survival curves for a proportional hazards model cannot cross, so that if one group is outperforming another, that trend will remain intact for the remainder of the study, according to the model.
A first hitting time model explains event times using a stochastic process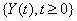 
that reaches a boundary B , also known as a threshold [3]. The first hitting time S of the data is given by
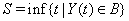
Note that {Y(t)} can be one- or multi-dimensional, could have different properties such as stationarity, independence of increments or a continuous sample path and has no guarantee of ever hitting the threshold, that is,
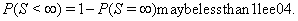
This stipulation accounts for censored subjects for whom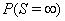 
is greater than 0. First-hitting time models do not require the proportional hazards assumption, giving them more freedom of application than corresponding proportional hazard models.
For a latent process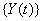 
, we have both process parameters and a baseline level. The process parameters, given as the vector 
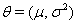outline the mean drift μ and the variance 
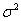.For simplicity, 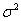is usually set to equal 1. The baseline level of the process, 
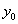, is simply the value of Y(0)
The data used usually consists of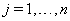 
subjects with independent health processes 
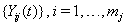where 
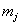is the final time recorded for subject j . The boundary sets of individual subjects may also vary, but for the purposes of this paper, we will assume a common threshold. For each of the n subjects, the data provide observation pairs
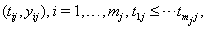
the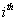
longitudinal reading 
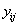on the level of
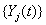at time 
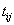,accompanied by an overall failure indicator 
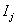which is 1 if 
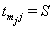and 0 if 
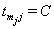. After the boundary set is reached, the level of the process, 
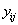is only read if 
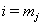,that is, if it is the first hitting time of the subject [4].
In many cases, longitudinal data are not available, so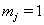 
for all j , and the only information available is the observation pair 
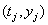and the failure indicator 
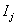,as above. In more extreme cases of restricted data, the only information available is 
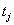,with 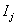conveying if the subject failed or was censored and when [4].
Each subject in a study contributes to part of the overall likelihood for the data, depending on whether the subject experienced a failure or was censored. If the subject fails at time S = s , then its contribution is given by
If the subject survives beyond the censoring time C , its contribution is given by
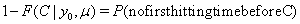
So, with a failure indicator 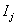, we have the likelihood function
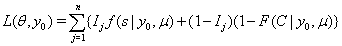
Multiple observations in survival data for a single subject are often decomposed into a series of smaller entries covering a set amount of time with initial and final data entries, creating a longitudinal sequence that can be used in first-hitting time models [1]. When longitudinal data, sequential observations on the same measurable time-varying covariates, are used, some useful properties arise that simplify the process of predicting survival. The sequence of time points for which observations are obtained is denoted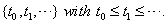
. This sequence ends when one of two events occur: the subject either fails or is censored.
The censoring time C will coincide with one of the time points in our sequence, so we can create both a failure code sequence
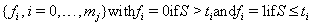
and a censoring code sequence
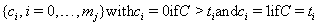
with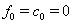 
These sequences lead to three possible code configurations at each time point. If the subject is surviving and has not been censored at time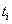 
,then 
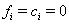.If the subject fails on or before time 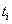,then 
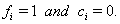If the subject has not failed by the censoring time, then 
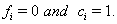These sequences are used in conjunction with the observable process sequence for the threshold-crossing variable given by 
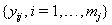and with the sequence of vectors of additional observed covariates, denoted 
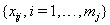for each subject j . Our assumptions require that these values are observed at the censoring time, but not after a failure.
Under a Markov assumption, we can assign baseline covariate values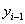 
and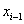 
to time increments 
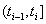to find the initial health status for the interval at time 
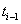.Let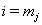 
be the last observation for a subject, that is, the first observation for which either 
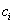or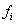 
is 1.With events 
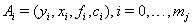,we have
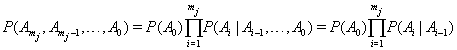
by the Markov assumption. By construction, the longitudinal record is broken into a series of one-step records with initial conditions for the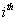 
entry given by 
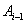and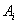 
as the final conditions on the interval. Explicitly, this is written as
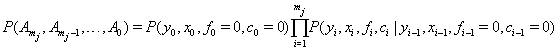
with 
unless the initial conditions are random [1].
Although many types of first hitting time models exist, some processes are used more often than others. One of the most common is the one-dimensional Wiener process with an inverse Gaussian first hitting time. The Wiener process has parameters μ and σ and begins with an initial value of Y(0) = 0 . When μ , the mean drift rate, is nonnegative,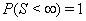 
,and the first hitting time S has an inverse Gaussian distribution. When μ is negative, 
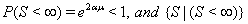has an inverse Gaussian distribution with parameters 
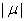and σ [4].
Another common process is the two-dimensional Wiener model for a marker and first hitting time. Here, the process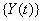 
is latent, but is accompanied by a marker process, 
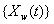that covaries with {Y(t)} in time. Jointly, the two processes form the two-dimensional Wiener diffusion process
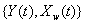that has initial values 
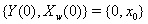and is distributed multivariate normally as
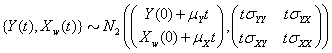
The threshold is set at 0, and the marker change process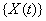 
is given by 
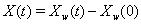[4].
The process is observed from the initial time 0 until the set censoring time C , so either the subject is surviving at C and the marker level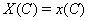 
is recorded or the subject fails at some time S and 
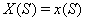is recorded.
A class of first hitting time models known as threshold regression models incorporate covariate data into the original first hitting time model using regression structures for the parameters of the process used [2]. In threshold regression, the effects on the hazard vary with time, so the proportional hazards assumption is not necessary [2]. Threshold regression institutes a regression structure that utilizes the same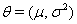 
process parameters with mean drift parameter 
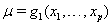and baseline level 
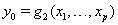. Here, 
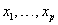are values of the covariates 
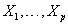for the subject and g1 and g2 are selected link functions for the data at hand. Many different link functions can be used, including linear and polynomial combinations of 
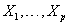, semiparametric regression splines, penalized regression splines, random effects models and Bayesian models [3].
The three building blocks of threshold regression, then, are: 1) the process,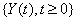 
,which could be a Wiener process, a Gamma process or some other applicable process; 2) the boundary, which could be a straight line or some curve; and 3) the time scale, which could be based on calendar time, running time or analytical time.
Threshold regression uses the log-likelihood function to determine survival time of a subject as follows:
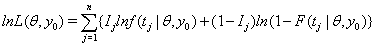
where 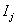is the failure indicator for subject j,tj is the censored survival time with 
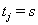if the subject failed, f and F are the first hitting time probability density function and cumulative distribution function, respectively [3].
Let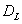 
be the event that the threshold B is eventually reached. Then the mean survival time for subject j can be found by
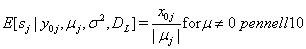
In Bayesian analysis, the nonidentifiability of these parameters can lead to either noninformative priors, which allows that parameter to drift to extremes, causing unstable estimates, or overinformative priors that do not allow for any Bayesian updating or learning [2].
In place of these problems, fixing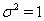 
allows us to model the remaining two parameters, 
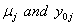using regression. Here, threshold regression reveals one of its greatest advantages: distinguishing between the two types of covariate effects [2]. Threshold regression designates its covariates as having an effect prior to the study, that is, on y0 , or as having an effect on the degradation of the subject, that is, on μ . A common regression structure uses the following equations:
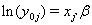
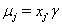
where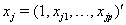 
is the covariate vector 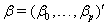and 
and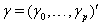 
are the respective covariate effects [2].
Using the SAS code from [5], we will investigate first a simple data set concerning myelomas, then a larger, similar data set regarding melanomas and finally an expansive data set dealing with ventilator-associated pneumonia in hospitals.
A hypothetical illustration of threshold regression involves 49 patients who have been diagnosed with myeloma, an accumulation of cancerous plasma cells. In this simple example, only three covariates accompany the time variable, measuring the time until death or censoring, and the failure indicator: the age of the patient at enrollment, the gender of the patient and the treatment applied to the patient [5]. These data are presented as highly restricted, so we are only given the value of these covariates at the end of the study and the time of failure or censoring. There is no opportunity to use longitudinal data or any Markov decomposition.
Using linear link functions, the program finds the coefficients for the expressions
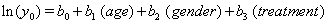
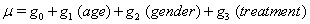
The Newton-Raphson method is used to maximize the log-likelihood function
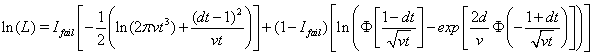
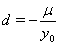
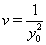
to retrieve the above coefficients. The nonlinear maximization procedure uses t -tests with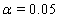 
to determine which coefficients are significant, and we obtain the following Table 1.
Table 1: The nonlinear maximization procedure uses t -tests with ñ = 0.05 to determine which coefficients are significant, and we obtain the following table.
Thus, we obtain the necessary regression coefficient estimates, yielding
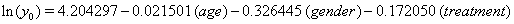
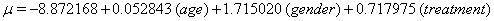
Using the lifetest procedure in SAS, we can obtain survival plots. We now compare these plots (Figure 1). with those generated by our regression.
Figure 1: Survival Curves by Gender.
According to our regression, gender is significant to both the initial health status y0 and the mean drift of the health process μ . Using the lifetest procedure in SAS, we see from the Kaplan-Meier survival estimates that males have a higher initial health status than females, but also that just before the median survival time the two curves cross twice. This means that near 3.3 years into the study, the males lost their health advantage, but quickly regained it. Males continued to out-survive females for the remainder of the study, with both groups having similar drifts, as evident by the close steepness in the two curves.
In our regression model, however, the females begin with a very slight advantage in initial health, but it is quickly lost when the female curve takes a steep turn downward. Both curves approach the threshold steadily, as in the lifetest procedure, and the median survival times are well predicted by the regression.
In our next set of curves ,(Figure 2), separated by treatment, we again focus on a variable that is significant to both y0 and μ . Using the lifetest procedure, we see that treatment 2 has a considerable disadvantage in initial health status. We also observe that all three curves cross each other multiple times, but are closest around 3.5 years after the study begins.
Figure 2: Survival Curves by Treatment.
This behavior is also found in our regression model, where the three curves reverse their order: treatment 0 goes from being the strongest to the weakest all within year three, while treatment 2 does the opposite. In our model, treatments 0 and 1 have approximately the same curve until the end of the third year. In all cases, the differences in the treatments are not evident until at least three years into the study, and the threshold is reached for both treatments 0 and 1.
Our second data set, from a true study of melanoma patients, is observed in the same way as the previous data, that is, with only one set of observations per subject. Here, the time until death or censoring is measured along with several covariates: sex of the patient, amount of inflammatory cell infiltrate (ICI), an epithelioid cell type indicator (ecells), an ulceration indicator, thickness of the tumor (mm) and age of the patient.
Again, linear link functions were used to solve for the coefficients of
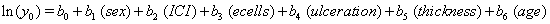
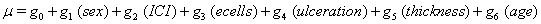
The same method is used to maximize the same likelihood function, and the coefficients are found and presented in the following Table 2, with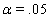 
, :
Table 2: The coefficients are found and presented in the following table with ñ = .05 .
These coefficients yield the functions
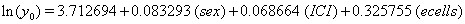
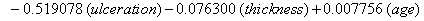
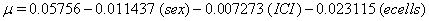
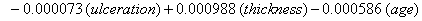
Our regression tells us that ulceration is significant only for y0 , the initial state of the health process of the patients. That difference is evident in the curves (Figure 3) provided by the lifetest procedure in SAS, but there also seems to be a rather large discrepancy between the drift of the two curves, which is absolutely not true in our regression. In the Kaplan-Meier estimates, the two curves do not cross, while in our regression model, the two curves are exactly the same. This holds for the insignificance of drift in our model, but does not account for the differences in initial health. The regression model does, however, accurately predict the median survival time for ulcerated patients and demonstrates that neither group reaches the threshold.
Figure 3: Survival Curves by Ulcerations.
The regression model states that the age of the patient is significant to both μ only. The age variable breaks the data into smaller groups, making some of the curves less informative. Groups with small sample sizes, such as those over 80 and those under 20, have curves that react strongly to a small number of failures, so these curves are often misleading in the Kaplan-Meier estimates. Accounting for this, we see that the differences in initial health are mostly due to these smaller groups and that there is otherwise a rather straightforward correlation between age and drift: the older the patient, the steeper the survival curve. It is also evident that earlier in the trial, before 1000 days, the survival curves of most of the age groups are rather tight, with much crossing and overlap, but after the 1000 day mark, the curves are considerably more separated, demonstrating that as time progresses, age plays a greater role in recovery and failure. It should also be noted that around 3000 days, the 40-80 year-olds have similar curves, but return to their previous pattern as the study progresses.
Our regression does not demonstrate any differences in initial health status, but is consistent with the major pattern found in the Kaplan-Meier estimates. Again, due to smaller sample sizes, the median survival times are not well-predicted for our data, but all the curves (Figure 4) stay well above the threshold, as is consistent with the data.
Figure 4: Survival Curves by Age.
In a recent study of ventilated patients taken to the intensive care unit (ICU) at a local hospital, 246 patients were observed to measure the time until ventilator-associated pneumonia occurred. Again, no longitudinal data were used, but one observation per subject was recorded with the time variable observed being the length of time on the ventilator and an indicator variable stating whether or not the patient contracted ventilator-associated pneumonia. The other covariates of note include: a chlorohexidine indicator (chx), the length of stay in the hospital in days (hstay), the length of stay in the ICU in days (icustay), the intubation site (intsite), an unplanned extubation indicator (uext), a reintubation indicator (reint), the age of the patient, the sex of the patient, the race of the patient, the admission diagnosis of the patient (adx) and a co-morbidity COPD indicator (copd). Note that a failure in this example is not a death due to a disease, but simply being diagnosed with ventilator-associated pneumonia, demonstrating that “failure" can have a number of meanings in first hitting time models.
Once more, linear link functions were used to solve for the regression coefficient given in
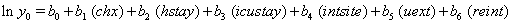
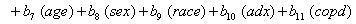
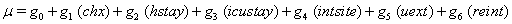
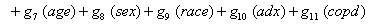
These link functions yielded the results in the following Table 3 with α = .05 :
Table 3: Linear link functions yielded the results in the following table with ñ = .05
So we have the functions
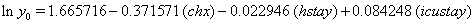
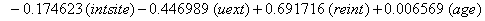
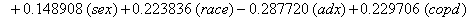
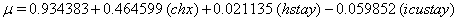
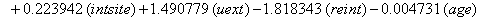
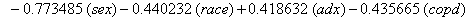
We will again compare the survival curves (Figure 5) for our regression with the Kaplan-Meier estimates generated by the lifetest procedure in SAS.
Figure 5: Survival Curves by Length of Stay in the ICU.
The regression output states that a patient’s length of stay in the ICU is significant only for the initial health status y0 . This variable is too varied to accurately depict all of the data, but with these limited sample sizes, we can see that the Kaplan-Meier estimates all have similar slopes for the first two weeks of the study. Furthermore, we can see that the initial health statuses do indeed differ, with those staying in the ICU for approximately two weeks outperforming those staying for three weeks by out three days, those staying for one week by about nine days and those staying for less than a week by more than ten days. In the Kaplan- Meier estimates, the only group reaching the threshold are those staying in the ICU for approximately one week.
In our regression model, all three curves have nearly the exact same drift, with very similar steepness of the curves. The differences in initial health are evident from the length of time each curve takes to first drop from the 100% survival rate. As in the Kaplan-Meier estimates, the curves for one week and three weeks are nearly identical, while that for patients staying in the ICU for approximately two weeks has the highest median survival time, around 13.5 days. It is noteworthy that a patient staying in the ICU for three weeks can still have a failure time prior to 21 days into the study, as a failure in this case does not indicate a death, simply the contraction of a disease.
The admission diagnosis of a patient is perhaps the most informative of the variables in this study, as it accounts for much of what happens to the patient after arriving at the ICU. The admission diagnosis is considered by our regression to be significant for both y0 and μ . The Kaplan-Meier estimates provided by the lifetest procedure display clear differences in the initial health statuses of patients from all eight groups, but it should again be noted that small groups sizes for some diagnoses, especially 6, 7 and 8 (post-operative, sepsis and miscellaneous, respectively), make for dramatic turns or a complete lack thereof in some curves. Even with a large sample size, though, patients admitted with cardiovascular diagnoses were then diagnosed with ventilator-associated pneumonia very quickly and often. The cardiovascular group reaches the threshold by day 11.
The regression model shows that the three most common diagnoses, neurology, pulmonary and cardiovascular, have closebut distinct curves (Figure 6), all of which reach the threshold by day 18. Patients initially diagnosed with neurological problems have an advantage over the other two in initial health, but have a steeper curve overall, showing the differences in mean drift of the processes. The differences in the drift for all the groups increase with time, as demonstrated by the drastic spread of the curves after day 8.
Figure 6: Survival Curves by Admission Diagnosis.
Finally, our regression marks reintubation of the patient as a significant variable for μ only. In the Kaplan-Meier estimates, reintubated patients have some advantage in initial health status, but the curve drops quickly, reaching the threshold by day 18. Patients for whom the variable was not applicable, meaning there was no unplanned extubation to reverse, decreased the most slowly, indicating that avoiding reintubation and unplanned extubation altogether will result in the strongest survival curve (Figure 7).
Figure 7: Survival Curves by Reintubation.
The regression model seems to display three different initial health statuses, but the significant differences lie in the drift of the processes. As expected, once the reintubated patient’s curve begins to drop, it drops quickly and almost straight down to the threshold. The small size of this group could lead to this dramatic drop, which is almost exactly mirrored by the non-reintubated patient’s curve approximately three days earlier. The large group, for whom reintubation was not an issue, has a less steep slope to its curve, overtaking non-reintubated patients by day 8 and reintubated patients by day 11, proving its significantly different mean drift.
Although the proportional hazards model has its uses, it relies too heavily on the proportional hazards assumption, which can fail quickly in application. In implementing threshold regression, a specialized case of the first hitting time model, this assumption is avoided, creating more opportunities for practice and function. Threshold regression models can also help to emphasize specific components that lead to changes in the health status of a subject by identifying significant and insignificant covariates as they are applied in regression [3].
Menu