Unravelling Textures of Mathematical Work in a High-Stakes Examination Context

Abstract

The ways in which examinees approach mathematics are significantly influenced by the context in which they operate. In this qualitative study the ways of working of, level 3 students from two Technical and Vocational Education and Training (TVET) colleges in South Africa were examined. The study focused on the end-of-year high-stakes National Certificate Vocational (NCV) examination as the contextual backdrop. To unravel the intricacies of examinees' work and their dialectic pursuit of solution-seeking, an ethnomethodological analysis was employed. In this study, "ways of working" refers to how examinees engage with mathematical content within the constraints of a time-limited, high-stakes examination. Due to the confidential nature of the high-stakes examination, a documentary analysis became necessary. Access to the written work of examinees was only permitted once the examination had concluded and the results had been published. The key findings of the study were as follows:

(1) The strategies employed by examinees are heavily influenced by the context of the high-stakes examination, and (2) The ways in which examinees approach their work demonstrate the typical structure observed in mathematical discourse practices. Further research is required to deepen our understanding of examinees' cognitive processes during time-constrained examinations.

Keywords

High-stakes examination; Algebraic fractions; Ethnomethodology; Resistance and accommodation; Abandonment

Introduction

Knowledge, whether helpful or not, and remembered during the years of schooling, particularly when studying for an examination, forms part of the objects stored in memory. Examinees are actively seeking solutions to mathematical problems posed to them to extract knowledge that is especially beneficial in the examination environment from all other previously gained knowledge. Examinees in a high-stakes examination or any other school-based assessment, on the other hand, are only permitted to reply to an examination question paper within a specific time frame, putting them under pressure to acquire and recall the correct information. The recognition that information is created and accessible in specific settings in this example, s high-stakes tests necessitates moving beyond an analysis of knowledge [1-3]. According to the scholars above, we should additionally examine the context and setting of the learning circumstances. For example, while accessing stored information to reply to mathematical problems in a high-stakes test, keep in mind that the examination room does not exist in isolation. Whether knowledge is obtained or recovered, knowledge retrieval through abandoned artefact in the NCV test is apparent in examinees' written replies and is a critical part of learners understanding of mathematics.

The NCV programme in TVET colleges offers a wide range of qualifications that aim to respond directly to the priority skills that will help the South African economy grow. Mathematics, as one of the fundamental subjects, becomes an obstacle if students struggle with it. This chapter provides an overview of literature that relates to the severity of a high-stakes examination, algebraic fractions as the key mathematics topic under analysis.

High-stakes examination

The NCV L3 mathematics, the end-of-year examination consist of all the characteristics to be labelled as a high-stakes examination. The mathematics NCV L3 examination is externally prepared by the Department of Higher Education and Training as a common examination in all provinces of South Africa. This examination is moderated externally and the students who fails this examination will not receive funding for mathematics to repeat the examination but will have to pay for the subjects themselves.

The NCV mathematics L3 high-stakes examination covers various topics in mathematics from which Algebra weighs 35%. The focus of this study is students’ ways of working with Algebraic Fractions in the NCV a high-stakes examination which forms part of the 35%. This study treats the topic under investigation and the context in which it is done as interconnected. Thus, all mathematical work produced are unobtrusively part of the examination room.

Fractional understanding vs. algebraic knowledge

In the field of algebraic understanding, there is a significant connection between students' struggle with fractional concepts and their struggle. When college students possess competence in working with fractions, it indicates their ability to navigate the various procedures involved in simplifying algebraic fractions. Furthermore, students who excel in fractions tend to perform well in algebra as well.

Conducted a study using quantitative methods to explore the potential link between rational number processing and algebraic ability. The findings of this study indicated a correlation between rational number understanding and algebraic performance, albeit depending on the type of knowledge being measured and the notation being used. Specifically, higher algebra fluency was associated with greater fluency in symbolic decimal magnitudes and stronger decimal ratio effects [4].

Errors and misconceptions

Argue that algebraic fractions pose significant challenges for students in the early stages of learning algebra, as they are multi-complex and contain various difficulties. Students tend to make numerous errors when working with rational algebraic fractions. These errors include cancellation errors, partial division, like term errors, equationisation, defractionalisation, and confusion with factors, dropping the denominator, failure to recognize common factors, common denominator errors, careless errors, inability to factorize trinomials, conjoining, and more [5-8].

Baidoo found that conceptual, mathematical language, procedural, and application errors hinder the appropriate understanding and application of algebraic fractions among grade 10 learners [9]. Permata highlighted learners' misconceptions that contribute to the errors they make when working with fractions [10]. These misconceptions include errors in integer addition, subtraction, division, multiplication with zero numbers, fraction addition, and fraction division.

Naicker analysed the conceptual and procedural difficulties that NCV L4 students displayed when working on factorization and solving mathematical problems that require factorization [11]. The results of the study showed that students experience both conceptual and procedural difficulties when working with any type of factorization. Problems included incorrect simplification of algebraic expressions; turning algebraic expressions into equations; failure to differentiate between an expression and an equation; failure to define in their own words the meaning of some foundational concepts such as factorisation, multiplication, expression, and equations. If students have challenges with factorization, they will surely experience challenges in simplifying algebraic fractions because factorization is one of the procedures usually required.

Based on the aforementioned studies, it is evident that learners commit numerous errors when working with algebraic fractions, stemming from their misconceptions about fractions and other mathematical procedures in various contexts. Learners require assistance in addressing these errors in order to progress effectively in algebra and mathematics as a whole.

The studies that have investigated learners’ ways of working with algebraic fractions have focused on what learners are doing right or wrong, looking at the types of misconceptions and errors that learners commit as they simplify algebraic fractions and the possible reasoning behind the errors committed in various context. This study employs an ethnomethodological analysis which do not judge examinees on the type of errors and misconception or which problems they got right or incorrect but rather focus on what is made visible through the textures of their solution-seeking pursuance in-situ. This study therefore was interested in teasing out the textures of work that are usually ignored and the feedback that can be gained from it.

Theoretical framework

The theoretical framework for this paper draws on the concept of ethnomethodology which looks at how ordinary people use common-sense knowledge, procedures, and considerations to gain an understanding of everyday situations [12]. Ethnomethodology is the study of practical action and practical reasoning in order to clarify a theoretical conception of social phenomena such as social order, social facts, social structures, reflexivity, accountability, and ethnomethodological indifference [13].

This paper uses ethnomethodology to explore the constitutive and situated nature of mathematical work. The objective of ethnomethodology is to extract social facts from practical social actions). The process of doing so is clarified in description of sociological studies, in which he established the objective reality of social facts as a fundamental principle of sociology [14].

From an ethnomethodological perspective, examinees as actors in the examination room produce mathematical work conduct themselves in such a way that makes visible the social facts. In turn, the social conditions (of high-stakes NCV examinations, in this case) determine what actors (examinees) do. All the properties of social order are thus made visible locally (in situ), with the result that social scientists and ethno methodologists can see what participants are doing agrees that the organisation of social order occurs naturally in its setting [15].

The concepts of social order and social action cannot be approached separately because they occur in a cyclical process, making the constitutive characteristics of social facts and social action an unavoidable part of mathematical production and making mathematical production details important [16]. Dourish emphasise the fact that practical social action attracts attention to how participants do it and how the production and understanding of social actions are formed "for practical purposes" [17]. Practical social action exists in all thinking processes and in the choice of mathematical skills selected to accomplish what was set out for the examinee to achieve.

Examinees’ solutions to mathematical problems are only part of the account of their understanding of mathematics, in terms of the totality of the natural occurrence in situ. The interaction of examinees and all relevant role players in the examination room is part of the distinctive, stable arrangement of the institution of the high-stakes NCV examination. In its exploration of examinees’ ways of working, this study analysed the dialectic production of mathematics within a social order and is concerned with responses that indicate how examinees go about doing the work and dialectically interpreting the examination questions in situ.

Pickering’s notions of resistance and accommodation

Pickering defines the "occurrence of a block on the path to some goal" as a form of resistance. This resistance is accommodated for by different ways of working. This dialectic resistance and accommodation are what Pickering call the Dance of agency. Thus sees accommodation as a tentative human approach that circumvents obstacles and through which the textures of abandonment were made visible.

This study therefore responded to the following research question: What are the characteristics of the dialectic resistance and accommodation in the solution seeking pursuance of L3 NCV students in the when responding to questions on Algebraic fractions in-situ.

Methodology

This study employed a qualitative research design and was underpinned by ethnomethodological constructs such as reflexivity, with the notion of building up accounts to make sense of the problem text and an overall approach of being non-judgemental, thus the idea of ethnomethodological indifference.

The researcher could not observe the participants in the examination room while doing the mathematics, because of the strict rules which govern the regularity of the high-stakes examination and the severity of the consequences for the examinees. Hence the analysis employed in this study was a quasi-ethnomethodological analysis.

A purposive sample was used for this study. This deliberate choice of participants was due to the qualities they possess [18]. The L3 NCV mathematics students have been selected specifically because they do algebraic fractions as part of their mathematics curriculum and are tested on it in their final examination.

Furthermore, these students achieved a mark of 30% and above in their continuous assessment programme during the year which gain them access to write the NCV high-stakes examination for mathematics L3. The L3 mathematics students used in this study were taken from two colleges TVET colleges in South Africa. One in Cape Town Western Cape Province and the second sample from a TVET college in Butterworth in the Eastern Cape Province. The data that was collected from the two institutions was the answer scripts from a group of L3 Engineering and related design students and boiler making students.

Denzin NK describes data as a set of interpretive and material practices that make visible that information which goes unseen [19]. For the purpose of this study 12 scripts was collected from the institution in Cape Town and 22 script from the Butterworth campus in the Eastern Cape Province.

All of the scripts were examined and assessed to find those with obvious textures, such as deletions and other elements suggesting that the examinees did not work in a linear method to answer algebraic fractions problems. This data selection procedure resulted in twenty-five scripts for detailed analysis.

The textures are classified according to their relevance to the research question. They were categorised based visible texture in the solution seeking pursuance. This study shows the findings and discuss four forms of abandonment:

• Reversal.

• Abandonment by pursuing the solution to a calculated procedure.

• Retracing the steps.

• Abandonment of the final result by showing the calculated resistance.

Results and Discussion

The agency in practise captures the dialectic of resistance and accommodation, where resistance denotes the failure to achieve an intended outcome. Accommodation is an active human response to resistance that can include concepts such as adaptations, inclusions, exclusions, among others. This occurs when there is a "looking back" or a revision of goals and intentions. When the resistance goes unnoticed, it is a case of non-firing of the resistance. What follows is the visible textures of examinees ways of working.

Reversal

"Reversal occurs when a calculated resistance is created, and the learner removes the produced work by drawing a line across it and subsequently begins again from a certain position" [20].

The way of working in Figure 1 below reveals the reversal after a calculated resistance was experienced. The examinee accommodated by cancelling the part of the pursuit and began again.

Figure 1: Reversal after a calculated resistance.

In Figure 1 the solution pursuance begins by writing down the algebraic fractions expression to be simplified in line 1 of 2.4.2. The pursuit continues in line 2 where the examinee factorised the expressions in the denominators (y²−16) and (y²−5y+4). The common factor in the second fraction (y+1) is then cancelled. In line 3 the solution from line 2 is written down with a small slip writing x and then cancelling it. In most cases when students work with algebraic fractions in class a variable x is the most commonly used? The examinee continues in line 4 and multiplied the numerator y with (y−5) from the denominator of the second fraction yielding to 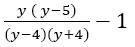In this instance the examinee treated the minus sign as an equal sign. The way of working with algebraic fractions shows a form of reflexivity, where teachers normally instruct learners to find the lowest common denominator, where cross multiplication is an option to accomplish that. A resistance experienced and line 4 is scratched out and the examinee start again in line 5 reversing back to line 3. The examinee cross multiplies the two fractions and use the denominator of the first fraction (y-1)(y+4) as a common denominator which is a procedure that is commonly used when solving rational algebraic equation.

Part of the examinees historicise mathematical knowledge the question “simplify” is an indication that they need to render on single fraction as an answer. With no equal sign between the two fractions cross multiplying does not yield the expected outcome.

The examinee then cancels (y-1)(y+4) in the numerator with that of the denominator as if they are common factors in the fraction yielding y(y-5)written in line 6.the line 7 the examinee simplifies by multiplying out the bracket from line 6 and gets y²-5y.The pursuit shows that the examinee attempted to produce a common numerator which rendered y²-5y. Which does not represent a fraction, the examinee drew straight lines (abandoning) the latter answer. Reversing back to line 3 and produce 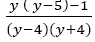in line 8 on the same solution seeking pursuit. The examinee rewrites the produced work in line 8 as the result in line 9.

Abandonment by pursuing the solution to a calculated procedure.

This way of working refers to the commencement of a pursuit to find a solution to a mathematical problem. The attempt shows some form of working up to a point where a procedure is produced and completely abandoned, then following on a path adjacent to the abandoned work. This pursuit shows an abandonment of the new attempt, followed by a continuation moving back to the initial solution seeking path.

Figure 2 shows an examinee’s way of working in which started in line 1 of 2.4.1 where the examinee wrote down the problem text. The solution pursuance begins in line 2 by changing the division sign to multiplication by inverting the fraction 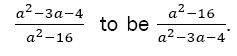The pursuit continues in line 3 and the examinee factorise the expression a²−3a − 4 in the denominator (line 2) to (a−4)(a−1) but left the other quadratic expression not factorised, at this point a resistance occurred. Thus, a non-firing of resistance occurs, and the examinee way of working continue to cross multiply the expression without factorising. The way of working used in line 4 was later abandoned and the examinee move to a position adjacent to the abandoned work to attempt to solve the procedure in line 3. In this new attempt the examinee multiplies all the numerators and all the denominators the fractions to get The examinee continued to expand by multiplied the first two factors of the numerator and also multiplying the first two factors of the denominator. The work done in line 5 was cancelled and the examinee move the adjacent to the abandoned work in the reversed back to the factors that were in line 4. The solution seeking pursuance continues in line 5 and the factors are multiplied and like terms cancelled. This way of working is understood to mean subtraction of like terms that have the same co-efficient which result to a zero answer. In line 6 the examinee opened the brackets in both the numerator and the denominator exerting agency in line 5 where like terms in the denominator were not added. The examinee accommodates for the resistance in line 5 and produce the procedure in line 7.The solution pursuance continues up to line 11 rendering 16a²-48a as the final result.

Figure 2: Abandonment during a calculated procedure.

The student’s cancelled is usually ignored by the lecturers and receive no mark allocation, through cancelling the student communicates to the lecturer that the work should be ignored. This shows an intelligible and accountable social order because it is a socially shared procedure. The lecturer, the student and the marker’s understanding that when a line or lines are drawn through, indicates that the work was an error or mistake which in the terms of accommodation and resistance, a student experienced a resistance and abandoned that work and a sought a different way of arriving to the desired solution. In an ethnomethodological view, the activities of scientists are in many ways similar to those of ordinary lay activities and ethnomethodology has deep interest and respect for practical rationality and accountability of the commonplace of ordinary activities .This way of working is similar to most common activities that ordinary members of society use. Cole CL further argues that ethnomethodology can do two things at the same time one is to show how a professional practice is embedded in quite ordinary competences and the other being to elaborate how it is special, in the sense of being part of a particular local version of a more generalized professional culture [21].

Retracing the steps.

Abandonment after assiduous effort towards a specific goal, removing selected produced work by going back over the same path to the source which did not comply with the dictates of the mathematical context. The source is adjusted, and the pursuit continues to produce a result.

In Figure 3 the examinee started in line 1 of 2.4.1 by writing the problem text. In line 2 the solution pursuance begins by changing the division sign to multiplication and inverting the fraction 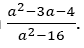In line 3 the examinee continues by factorising the quadratic expressions in the numerators and denominators. Resistance is encountered and the way of working is then abandoned and cancelled which is shown by a line through the work. The examinee reverse (first reversal) and re-factorise a²−a as difference of two squares and get (a-a)(a+a)and then continue to write the second fraction 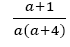with a²+4a factorised correctly to a(a+4). The last [what last fraction fraction] is also written in line with its quadratic expressions in the numerator factorised, a²−16=(a−4)(a+4) and the denominator a²−3a−4=(a−1). The resistance in sign (-1) factors of a²−3a−4 was not noticed and the examinee continued with the solution pursuance in the same path. In line 4a the examinee writes the outcome after cancelling the common factors (a−4)(a+4) and (a−1) in line 3. The outcome written in line 4a is 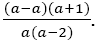The solution pursuance continues in line 5a, and the examinee open the brackets a(a-2) and a²-2a.The solution path does not yield the desired results, the examinee then (second reversal) back to line 3 to first way of working that was abandoned a U-turn was taken. The quadratic expression a²-a that was factorised as a(a-1) and then cancelled is now used in line 4b and the factors (a−a)(a+a) are abandoned and cancelled with an indication of a line crossed through in line 3 and 4a. Another line is cancelled through line 4a and 5a to indicate that all that solution path is abandoned. The solution pursuance begins again from line 4b and the factor(a+1) , in line 5b the examinee simplifies by eliminating the brackets and yields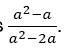The examinee in line 5b cancels the unknown "a" as common. This way of working is referred to as convenience and will be discussed later a²'s and a's are cancelled leaving the solution a s1/2. The solution was the expected outcome from the examinee, and it was left as the final solution.

Figure 3: Examinee's Solution Pursuance for Algebraic Expression in retracing the steps.

Abandonment of the final result by showing the calculated resistance Abandonment refers to the commencement of solution seeking path and before completing the pursuit the solution is abandoned; the student starts a new way of working to create a new problem.

Figure 4: Abandonment of final result by showing the calculated resistance

In Figure 5 shows examinees way of working with visible textures of abandonment. The examinee started in line 1 by writing the problem text. A solution seeking path commences in line 2 by first factorising the quadratic expressions a²+4a in the denominator. This is followed by the second expression, a²−3a−4, the numerator of the third fraction followed by a²-16 in the denominator of the last fraction. The way of working in factorising the fraction follows two procedures, factorising by taking out the common factor and factoring the difference of two squares. In line 2 when factorising the expression a²+4a, resistance is experienced, this is followed where the examinee first takes out the common factor a the dance of agency leads to taking a step back to observe the performance. There is resistance and before completing the factorisation the way of working is abandoned. In Line 3, the expression a²−16 did not have a common factor but the examinee way of working showed convenience because with a as a factor in the numerator and denominator it then be easy to cancel it out. The solution pursuit continues and a²−a is factorised by taking out the common factor. After factorising this expression, the examinee makes a U-turn, reconsider how a²+4a was factorised and redo the factorisation by taking out the common factor. In line 3 the examinee further changes the division sign to multiplication, without indicating it as a multiplication sign, by inverting the fraction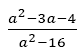 which was factorised as 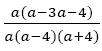is inverted to be 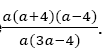The factors of a²−3a−4= a(a−3a−4) are also reconsidered and changed to a(3a−4) After line 3 the whole solution is abandoned. The examinee cancels it by show of drawing two lines across the solution. The examinee starts again by copying line 4 from line 1. The examinee starts over by first factorising a²+a and a²+4a by taking "a" out as a common factor. The third fraction in line 4 is first written as a reciprocal and then both numerator and denominator are factorised. The denominator a²−3a−4=a(a−3a−4), the common factor is only factored out in the first term a². the other term 3a−4 are left the same. The numerator a²−16 is factorised by using difference of two squares becoming (a+4)(a−4). The examinee cancelled the a in the first and second fraction and also re-doing the factorisation of a(a−3a−4)into (a+4)(a−4).

Figure 5: Calculated resistance circled.

Figure 6: The texture (arrow) to direct the flow of solution pursuance.

In Figure 6 shows line 5, 6 and 7 the way of working in factorising a²−3a−4 is abandoned and the factors a(a−3a−4) are changed to (a+4)(a−4) and written in line 6. In 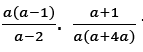the common factor ais cancelled and solution 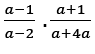is is written in line 6. In line 7 an equal sign is written which shows the examinee has not reached the last step of the solution but the solution seeking path is abandoned and left without a result.

Figure 6 above show an example of abandonment observed in an examinee’s script. The examinee in line1 wrote the problem text. In line the solution seeking path begins, the quadratic expressions are factorised and the division is changed to multiplication by inverting the fraction 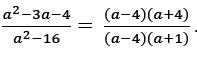Further in line 2 the examinee cancels the common factors from 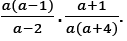The solution is written in line 3 as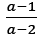

but this solution path is abandoned before it was written in full and the examinee cancels line 2 and line 3 and used an arrow to direct the marker to line 4 which where the solution pursuance commences after abandoning the first attempt. The solution pursuance follows the same path that was taken in the previous attempt but this time the expression a²−16 is not factorised. The path continues in line 5 and now all the quadratic expressions in the fractions are factorised and all common factors cancelled. The last step of the solution is written in line 6 which is the same expression in line 3 [22-25].

Conclusion

This study has contributed towards exposing the practises that learners engage in when solving mathematical problems in high-stakes examinations. It has shown how examinees engaged with the problem text, resulting in various ways of working along solution-seeking paths. The students’ ways of doing mathematics in a high-stakes examination context resembles a mathematician-like way of working. As suggested by Schoenfeld, it should be the aim of mathematics educators to introduce learners to such mathematics practices. Smith goes further, asserting that learners should be given the opportunity to practise this mathematician-like way of doing mathematics at their own level.

In addition, the study adds value to the type of feedback generated within the high-stakes NSC mathematics examination. It illustrates an alternative type of feedback, which can be extracted from the learners’ ways of working with algebraic fractions. Furthermore, this study has contributed to the drive of the South African Department of Basic Education (DBE) to improve mathematics results in our schools.

Furthermore, teachers need to see examples, such as the abandoned work presented in the analysis, as a useful object of teaching and learning. When teachers allow learners to make sense of this solution-seeking process, it will foster a greater understanding of their own ways of working in a time-restricted examination. According to Lampert the content of mathematical lessons should expose learners to mathematical contexts that expose them to strategies that support or reject solutions instead of simply searching for the answer. This way of doing mathematics should furthermore encourage interaction between learners to discuss their solution-seeking strategies. The resulting meaning-making will give learners a greater understanding of their own ways of working. This process of getting learners to analyse, explain, and interpret when they abandon an approach will also provide learners with more direct feedback, which will in turn improve their understanding of their own work in a specific mathematical context.

Watson contend that the use of such mathematical objects, even in highly structured situations in which learners seek the same answers or practical accomplishments using the same data, may provide learners with experiences. It would allow teachers to plan their teaching from the learners’ perspectives.

Future research may involve the practise of encouraging collaborative group work among learners to ascertain the strategies learners employ when analysing and interpreting responses taken from school-based assessments, such as class tests and examinations, as well as responses from high-stakes examinations. In addition, further studies are required to deepen the understanding of the thinking processes of examinees by, for instance, conducting focus group interviews where examinees are afforded opportunities to explain their workings in a school-based assessment.

References

1. Lave J. Cognition in practice: Mind, mathematics and culture in everyday life. Cambridge University Press; 1988 Jul 29.
2. Lerman S. The social turn in mathematics education research. Multiple perspectives on mathematics teaching and learning. 2000;1:19-44.

   [Google Scholar].

3. E. Wenger. Communities of practice: learning as a social system. Systems thinker. (1998);9:2-3.

   [Google Scholar].

4. Hurst MA, et al. Children’s understanding of fraction and decimal symbols and the notation-specific relation to pre-algebra ability. J Exp Child Psychol. 2018;168:32-48.

   [Crossref] [Google Scholar] [Pub Med].

5. Jacobs M, et al. Item difficulty analysis of a high-stakes mathematics examination using Rasch analysis. Pythagoras. 2014;35:1-7.

   [Crossref] [Google Scholar]

6. Figueras, et al. Doing Mathematics—What does it mean? Unpublished keynote address presented at the Second Annual Convention of the Mathematics Association of Transkei Transkei Inservice College: Mthatha. 2008.
7. Makonye JP, et al. Eliciting learner errors and misconceptions in simplifying rational algebraic expressions to improve teaching and learning. Int J Educ Sci. 2016;12:16-28.

   [Crossref] [Google Scholar].

8. Makonye JP, et al. Probing grade 10 students about their mathematical errors on simplifying algebraic fractions. Research in Education. 2015;94:55-70..

   [Cr­ossref] [Google Scholar].

9. Baidoo J. Dealing with grade 10 learners’ misconceptions and errors when simplifying algebraic fractions. J Emerg Trends Educ Res Policy Stud. 2019;10:47-55.

   [Crossref] [Google Scholar].

10. Permata D, et al. Students’ misconceptions on the algebraic prerequisites concept: causative factors and alternative solutions. J Phys Conf Ser. 2019;1265:012005).

    [Crossref] [Google Scholar].

11. Naicker AS. Conceptual and procedural difficulties experienced by National Certificate vocational level 4 students in solving factorisation problems at a Kwazulu-Natal technology centre. Unpublished Master of Education “Thesis”. University of South Africa. 2017.

    [Google Scholar].

12. Garfinkel H. Studies in ethnomethodology. Social Theory Re-Wired. Routledge, 2023;58-66.

    [Google Scholar]

13. Garfinkel H. "Respecification: Evidence for locally produced, naturally accountable phenomena of order, logic, reason, meaning, method, etc. in and as of the essential haecceity of immortal ordinary society (I)—an announcement of studies." Ethnomethodology and the human sciences. 1991;10-19.

    [Crossref] [Google Scholar].

14. E. Durkheim The Rules of Sociological Method. Glencoe, Illinois: The Free Press. 1950.

    [Google Scholar].

15. Liberman K. Semantic drift in conversations. Hum Stud. 2012;35:263-277.

    [Crossref] [Google Scholar].

16. Coulon. Ethnomethodology Sage Publications. 1995.
17. Dourish P, et al. On" technomethodology": Foundational relationships between ethnomethodology and system design. Hum Comput Interact. 1998;13:395-432.

    [Google Scholar].

18. Etikan I, Musa SA, Alkassim RS. Comparison of convenience sampling and purposive sampling. Am J Theor Appl Stat. 2016;5:1-4.

    [Crossref] [Google Scholar].

19. Denzin NK, et al. The SAGE handbook of qualitative research Sage. The Department of Basic Education (DBE) (2011). Curriculum and assessment policy statement: Grades 10–12. Pretoria: Mathematics. 2011.  
20. Julie C. Work moments in mathematical modelling by practising mathematics teachers with no prior experience of mathematical modelling and applications. N Z J Math. 2003;32:117-124.
21. Cole CL. Paul ten Have (2004). Understanding Qualitative Research and Ethnomethodology. Forum Qual. 2005;6.

    [Crossref] [Google Scholar].

22. Schoenfeld AH. Cognitive science and mathematics education. Psychology Press.1987.

    [Google Scholar]

23. Smith R, et al. Professional learning communities, professional learning and the role of relational agency. Caught In The Act: Reflections On Continuing Professional Development Of Mathematics Teachers In A Collaborative Partnership. 2019:131.

    [Google Scholar].

24. Lampert M. When the problem is not the question and the solution is not the answer: Mathematical knowing and teaching. Am Educ Res J. 1990;27:29-63.

    [Crossref] [Google Scholar].

25. Watson A, et al. Seeing an exercise as a single mathematical object: Using variation to structure sense-making. Math Think Learn. 2006;8:91-111.

    [Crossref] [Google Scholar].