ISSN: 2320-2459
ISSN: 2320-2459
Osman Muhammed Ahmed*
Department of Physics, Debre Tabor University, Debre Tabor, Ethiopia
Received Date: 17/09/2018; Accepted Date: 23/12/2018; Published Date: 30/12/2018
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
In this paper I have found the magnetic field strength of a neutron star, by using flux conservation, which the size of the sun as a progenitor star and its magnitude is Bη=9 × 1014 G which is approximately quadruple of magnetic field of the sun. The dying star collapses to form a neutron star, magnetic flux conservation results in the formation of regions of extremely strong magnetic field near the neutron star. This shows a neutron star is strongly magnetized at birth. This kind of neutron star is called a pulsar and it is supposed radiator. The rotation period of a neutron star is calculated using angular momentum conservation and the result led that, the rotation period of neutron star is τηs ∼ 0.1 s. The sun rotates once every 107 seconds; this implies that a typical neutron star with radius 10 km rotates 108 times faster than the size of our sun with radius 105 km. So a typical neutron star is a pulsar.
I have derived the field lines corresponding to a magnetic octupole moment. 2D case-section of the field lines of a neutron star is drawn. The magnetic field of a neutron star is derived from flux conservation and is high during the age of its birth. The octupole magnetic field of a neutron star is maximum at the surface and ceases to zero in the far distant zone, but visible as pair lobes looks like dipole.
Finally, the octupole field strength is dominated at the surface than the dipole field, this leads to Neutron stars octupole field near the center is more significant. The radiation from such a source is calculated and is shown to be diffuse. The radiation pressure generated from octupole field lines of neutron star is calculated and the pressure dominates at the surface and rapidly drops it in the far zone. This result leads to violate the known electromagnetic radiation in the far zone is not vanish rapidly. So, this is the neutron star’s unique property, with evidence supported by two rotating axis than other stars with one rotating axis.
Octupole, Neutron star, Magnetic flux, Radiation pressure
In 1934 Walter Baade and Fritz Zwicky proposed the existence of neutron stars, only a year after the discovery of the neutron by Sir James Chadwick. In seeking an explanation for the origin of a supernova, they proposed that the neutron star is formed in a supernova explosion. Neutron stars are about 20 km in diameter and have a mass of about 1.4 times that of our Sun. This means that a neutron star is so dense that on Earth, one teaspoonful would weigh a billion tons [1-3].
Because of its small size and high density, a neutron star possesses a surface gravitational field about 2 × 1011 times that of Earth. Neutron stars can also carry magnetic fields a million times stronger than the strongest magnetic fields produced on Earth. Neutron stars are one of the possible end states for a massive star. They result from massive stars which have mass greater than 6-8 times that of our Sun. After these stars have finished burning their nuclear fuel, they undergo a supernova explosion. This explosion blows off the outer layers of a star into a beautiful super- nova remnant. The central region of the star collapses under gravity. It collapses so much that proton and electron combine to form neutrons [1-3].
In 1967, Jocelyn Bell and Antony Hewish discovered regular radio pulses from CP 1919. This pulsar was later interpreted as an isolated, rotating neutron star. The energy source of the pulsar is the rotational energy of the neutron star. Neutron stars are very dense, which means that they are very compact the size of a small object with a diameter of ≈20 km. This property results in the neutron star’s gravitational force to be very powerful. The gravitational force of a neutron star is so powerful, “that if one drops a marshmallow on to a neutron star, the impact of the marshmallow on the surface of the neutron star would be comparable to that of a small atomic bomb hitting the earth’s surface.”
A neutron star also has two axes: a magnetic one and an axis of rotation. Besides emitting radio waves, a neutron star also emits intense X-rays and γ-rays as well. In fact, Neutron stars emit some of the strongest X-rays in our galaxy. Neutron stars are strongly magnetized fast rotating objects. As a result a neutron star can generate immensely huge potential differences. This helps neutron stars pulse strong radiation from its two poles. Also, along with rotation, the magnetic field can produce potential differences of trillions of volts [1,4].
Electromagnetic radiation is made up of electric and magnetic fields that oscillate at right angles to each other. EM radiation moves at a speed of light c. The Poynting vector S is defined as to be equal to the cross product 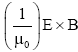 . where μ0, is the permeability of the medium through which the radiation passes, E is the amplitude of the electric field, and B is the amplitude of the magnetic field. Applying the definition of cross product and the knowledge that the electric and magnetic fields are perpendicular to each other gives the magnitude S of the Poynting vector as
. where μ0, is the permeability of the medium through which the radiation passes, E is the amplitude of the electric field, and B is the amplitude of the magnetic field. Applying the definition of cross product and the knowledge that the electric and magnetic fields are perpendicular to each other gives the magnitude S of the Poynting vector as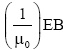 . where E and B are, respectively, the magnitudes of the vectors E and B. There is electric and magnetic multi-pole radiation of all order. Here is our attention is focused on specially octupole magnetic radiation. The pressure pushing outwards from the centre of an ordinary star because of the energy generated at the stars core counterbalances the gravitational forces due to the stars mass which tend to make it contract. When the stars energy production ceases and the radiation pressure is removed, the star will start to collapse [5-7].
. where E and B are, respectively, the magnitudes of the vectors E and B. There is electric and magnetic multi-pole radiation of all order. Here is our attention is focused on specially octupole magnetic radiation. The pressure pushing outwards from the centre of an ordinary star because of the energy generated at the stars core counterbalances the gravitational forces due to the stars mass which tend to make it contract. When the stars energy production ceases and the radiation pressure is removed, the star will start to collapse [5-7].
These special characteristics of neutron star from other ordinary star makes our attention to study and measure the magnetic field strength, its field lines emanating from its centre and the radiation pressure from its octupole fields, especially, the obliquely rotating magnetic moment (Figure 1) [8].
In this paper we have used analytical method to get the geometry of octupole filed lines and to derive the magnetic flux of a neutron star. In some analytical purposes, we have used Wolfram Mathematica software to simplify tricky trigonometric equations.I have used python 2.7 and matplotlib to plot and interpret our data.
Flux Conservation
Rotating neutron stars formed in a supernova explosion in which massive stars die explosively. In the process the residual magnetic field of the star gets conserved in the neutron star which is formed after the explosion (Figure 2). As a result the intensity of the magnetic field of the progenitor star will intensify inside the neutron star to a high level. We demonstrate this as follows; Let as assume that the progenitor star is as big as our sun whose surface magnetic field is known to be ∼104 G. The magnetic flux corresponding to this is:
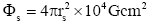
where rs is radius of the sun
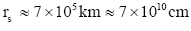
Hence
Φs ≈ 9 × 1026 Gcm (2)
Flux conservation is that neutron star magnetic fields are remnants of the field of their progenitors. By the principle of flux conservation we expect:
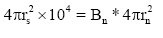
where Bn is the surface magnetic field of the neutron star and rn is the radius of the neutron star which known to be of the order 10 km=106 cm. Hence
Bn=9 × 1014 G (3)
The magnetization vector associated with this magnetic field is usually an oblique rotator. Since m is oblique the vector potential is rotated at any field is sinusoidal and hence time. This kind of neutron star is called a pulsar and it is supposed radiator.
Angular Momentum Conservation
A rotating object has angular momentum L, given by L=Iω where I is the moment of inertia and ω is the angular velocity. ω is the angle in radians through which an object rotates per unit time. If the rotation period is τ then 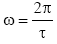 .
.
The moment of inertia of a uniform sphere of mass M, radius R is 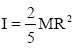 . Therefore, before its collapse to a neutron star, the core of a progenitor star will have an angular momentum
. Therefore, before its collapse to a neutron star, the core of a progenitor star will have an angular momentum 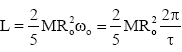
Angular momentum (and core mass) is conserved during the collapse, so after the neutron star forms it will have the same L: 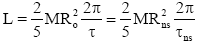 So the rotation period of the neutron star will be given by
So the rotation period of the neutron star will be given by
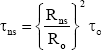 (4)
(4)
Suppose the core of a typical dying star has a radius of ∼105 km and rotates once every ∼100 days i.e. ∼107 s. Then after collapsing to a neutron star of radius ∼10 km it will have a rotation period of τηs ∼ 0.1 s. So we have an object of about the mass of the Sun, rotating 10 times every second (Figure 3).
Components of Octupole Magnetic Field
Consider a charge Q uniformly distributed over a surface of spherical neutron star of radius R. Assume that a neutron star is spinning with a frequency of ω about its diameter (Figures 4 and 5). We would like to calculate the magnetic field generated by the spinning charge at external to the body of the neutron star (Table 1).
Table 1: The value of octupole and dipole magnetic field strength.
| Distance(cm) | |B1|(G) | |B1|(G) | |B3|(G) | |B3|(G) | ϑ(degree) |
|---|---|---|---|---|---|
| 1 × 106 | 4.2 × 1014 | 2.2 × 1014 | 4.5 × 1014 | 9.5 × 1014 | π/4 |
| 2 × 106 | 5.3 × 1013 | 2.6 × 1013 | 1.4 × 1013 | 3 × 1013 | π/4 |
| 3 × 106 | 1.6 × 1013 | 7.8 × 1012 | 2.6 × 1012 | 4 × 1012 | π/4 |
| 4 × 106 | 6.6 × 1012 | 3.3 × 1012 | 4.3 × 1011 | 9.8 × 1011 | π/4 |
| 5 × 106 | 3.4 × 1012 | 1.7 × 1012 | 1.5 × 1011 | 3.2 × 1011 | π/4 |
| 6 × 106 | 2 × 1012 | 9.8 × 1011 | 6 × 1010 | 1.3 × 1011 | π/4 |
| 7 × 106 | 1.2 × 1012 | 8.7 × 1011 | 2.7 × 1010 | 6 × 1010 | π/4 |
From the vector potential expansion, we have the general multi-pole
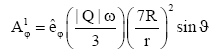 (5)
(5)
and
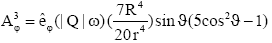 (6)
(6)
where eqns. (5) and (6) are the dipole (l=1) and octupole (l=3) vector potentials respectively
The magnetic field components in a spherical coordinate system are
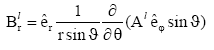 (7)
(7)
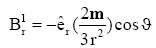 (8)
(8)
Substituting eqn. (5) in to eqns. (7) and (8) it reduces to
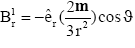 (9)
(9)
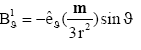 (10)
(10)
where 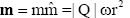 is the dipole moment. A neutron star total magnetic field is given by
is the dipole moment. A neutron star total magnetic field is given by
Bη=Bd+Bq+Bo+Bhot (11)
Magnetic field of a neutron star, from flux conservation derived earlier we have
9 × 1014 G=Bd+Bq+Bo+Bhot (12)
Assume that
Bn ≈ Bd
We know that the dipole magnetic field of a neutron star can be calculated as
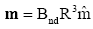
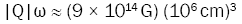
Therefore
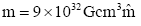 (13)
(13)
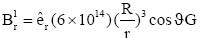 (14)
(14)
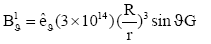 (15)
(15)
In a similar fashion insert eqn. (6) into (7) and (8) the octupole magnetic field components are:
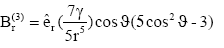 (16)
(16)
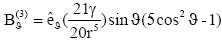 (17)
(17)
where 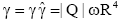 is the Octupole moment. Following the same fashion for the octupole magnetic field, to be show as follows.
is the Octupole moment. Following the same fashion for the octupole magnetic field, to be show as follows.
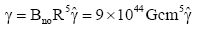 (18)
(18)
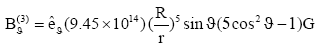 (19)
(19)
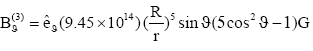 (20)
(20)
The Octupole Magnetic Field Lines
A magnetic field is a field of force produced by moving electric charges or by electric fields that vary in time. The magnetic field at any given point is specified by both direction and magnitude (Figures 6 and 7). The relationship between the magnetic and electric fields, and the currents and charges that create them, is described by a set of four so called Maxwell’s equations.
In spherical coordinates
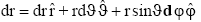 (21)
(21)
In the same way 2D magnetic field can be written as
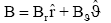 (22)
(22)
Divide the corresponding terms of eqn. (21) by those in eqn. (22) to got
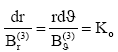 (23)
(23)
where KO is a constant related to the field curvature. The above equation can be rewritten as
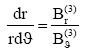 (24)
(24)
Substituting eqns. (16) and (17) in to the above equation for the magnetic dipole field, we obtain
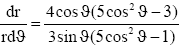 (25)
(25)
Rearranging and integrating the above equation we find
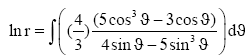 (26)
(26)
Multiplying this equation by cos ϑ and using some trigonometric identities, we got
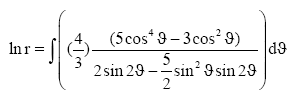 (27)
(27)
Let us now define a constant e by
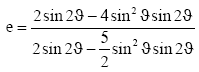
Multiplying eqn. (27) by (e) we find
 (28)
(28)
Let us now define a constant n
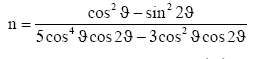
Multiplying eqn. (28) by 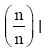 find
find
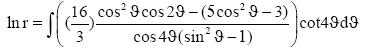 (29)
(29)
Integrating by parts and we have used Mathematica Wolfram in three parts to simplify the main equation, finally we have
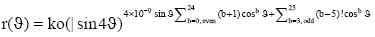 (30)
(30)
This equation is the general field line equation for the magnetic octupole field as a function of ϑ.
Radiation Pressure of Neutron Star
When the stars energy production ceases and the radiation pressure is removed, the star will start to collapse. For a system of charges and currents varying in time we can make a Fourier analysis of the time dependence and handle each Fourier component separately. Considering the potentials, fields, and radiation from a localized system of charges and currents that vary sinusoidally in time:
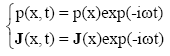
The solution for the retarded vector potential in the Lorenz gauge is
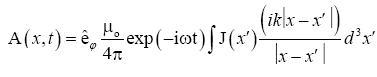 (31)
(31)
where k=ω /c is the wave number, and a sinusoidal time dependence is understood. The magnetic field is given by
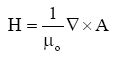 (32)
(32)
While, outside the source, the electric field is
 (33)
(33)
where 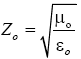 is the impedance of free space. If the source dimensions are of order d and the wave-length is λ=2πc/ω, and if d ≪ λ, then the far (radiation) zone d ≪ λ ≪ r. Our emphasis is in the far zone. In the far zone (kr ≪ 1) the exponential in equation oscillates rapidly and determines the behaviour of the vector potential. In this region it is sufficient to approximate
is the impedance of free space. If the source dimensions are of order d and the wave-length is λ=2πc/ω, and if d ≪ λ, then the far (radiation) zone d ≪ λ ≪ r. Our emphasis is in the far zone. In the far zone (kr ≪ 1) the exponential in equation oscillates rapidly and determines the behaviour of the vector potential. In this region it is sufficient to approximate
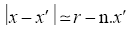
where n is a unit vector in the direction of x. For a far zone r is dominated, then the vector potential is
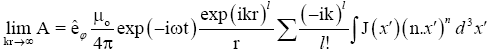 (34)
(34)
Poynting Vector from Octupole Fields
The third term or (l=3) in expansion (34) leads to an octupole vector potential,
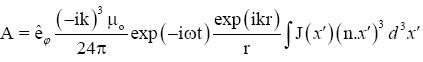 (35)
(35)
Magnetization due to the current J;
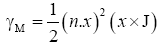 (36)
(36)
Recall that γ calculated in eqn. (18), and inserting in to this equation, we find
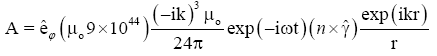 (37)
(37)
where γ is the magnetic octupole moment,
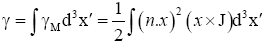 (38)
(38)
The complete fields are somewhat complicated to write down. Our aim is the fields in the radiation zone. Then it is easy to see that
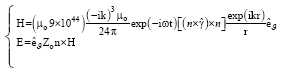
The average poynting vector for the magnetic octupole fields is
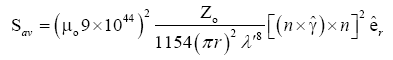 (39)
(39)
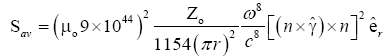 (40)
(40)
The time-averaged intensity Sav divided by the speed of light in free space is the radiation pressure exerted by an electromagnetic wave on the surface of a target:
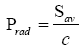 (41)
(41)
Substituting eqn. (39) in to eqn. (41) the magnetic octupole radiation pressure becomes
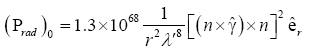 (42)
(42)
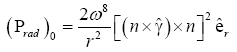 (43)
(43)
This is the radiation pressure in the radial direction.
In this paper I have found the magnetic field strength of a neutron star, by using flux conservation, which the size of the sun as a progenitor star and its magnitude is Bη=9 × 1014 G which is approximately quadruple of magnetic field of the sun [9-11]. The dying star collapses to form a neutron star, the magnetic flux conservation results in formation of the regions of extremely strong magnetic field near the neutron star. This shows a neutron star is strongly magnetized at birth. This kind of neutron star is called a pulsar and it is supposed radiator. The rotation period of a neutron star is calculated using angular momentum conservation and the result led that, the rotation period of neutron star is τηs ∼ 0.1 s. The sun rotates once every 107 s, this implies that a typical neutron star with radius 10 km rotates 108 times faster than the size of our sun with radius 105 km. So a typical neutron star is a pulsar [12-15].
I have derived the expression for the octupole magnetic field starting from the vector potential A. A multipole expansion of A, led in to the expression for the octupole field, and it is dominated at the surface and decreases rapidly in the far distance as shown in Figure 5. The quadrupole magnetic field strength of a neutron star should lie between the dipole and octupole fields [16]. This is in contrary to the electromagnetic radiations emitted by other stars [17-20]. The field lines from these magnetic field is calculated and shown that the field lines form eight loops with an angular span of 2π as shown in Figure 6.
Finally, I have derived the radiation of this component to show that its pressure is radial having inverse distance square dependence. The radiation pressure from a neutron star varies as the 8th power of the frequency for octupole fields [21,22]. As shown in Figure 8, the octupole radiation is high near the surface of a neutron star for both X-ray and γ-ray frequencies. Since the radiation pressure of a neutron star is derived from retarded vector potential expansion, electromagnetic potentials and fields are assumed to have the same time dependence [23]. So it is gauge invariance (Table 2).
Table 2: Radiation pressure from octupole field in γ and X rays range.
| r (m) | (PO)γ−ray | (PO)X−ray |
|---|---|---|
| 1 × 104 | 4.8 × 10174 | 4.8 × 10142 |
| 2 × 104 | 1.2 × 10174 | 1.2 × 10142 |
| 3 × 104 | 5.3 × 10173 | 5.3 × 10141 |
| 4 × 104 | 3 × 10173 | 3 × 10141 |
| 5 × 104 | 2 × 10173 | 2 × 10141 |
| 6 × 104 | 1.3 × 10173 | 1.3 × 10141 |
| 7 × 104 | 9.8 × 10172 | 9.8 × 10140 |
In the future we will consider 3D octupole field lines and magnetic field strength of a neutron star.
I would like to express my gratitude to all those who gave me encouragement and support to complete this research, especially, the late died scientist Dr Legesse Wetro, his supporting ideas are high in this research (R.I.P.) I would like to say also thanks Dr Abraham Amaha for his valuable comments.