ISSN: 2320-2459
ISSN: 2320-2459
Independent Researcher, PhD in Mechanical Engineering, Italy
Received Date: 01/04/2016; Accepted Date: 27/04/2016; Published Date: 30/04/2016
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Among the various models of Universe commonly considered, the so called oscillatory class stands out. A Universe that oscillates following a simple harmonic motion evidently belongs to the above-mentioned class. The aim of this paper simply consists in deducing, in this specific case, the well known Friedmann-Lemaître relations without using Einstein field equations. Homogeneity and isotropy are obviously taken for granted.
Oscillating Universe, Cosmological Constant, Friedmann–Lemaître Equations, Alternative Deduction
Let's suppose that our Universe could oscillate following a simple harmonic motion. If we denote with R the radius of curvature, with Rm the amplitude of the motion (the mean radius), and with c the speed of light, we can write, with obvious meaning of symbols and signs, the following:
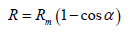 (1)
(1) 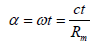 (2)
(2) 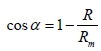 (3)
(3) 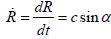 (4)
(4) 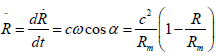 (5)
(5)
Due to the symmetry, we have to consider, in defining the density, half the volume of a three-dimensional ball: each material point, in fact, has to be considered as linked to its antipode (the point diametrically opposite) [1]. As a consequence, if we denote with Mm the mass of the Universe (actually half the value of the mass-energy) when the radius of curvature is equal to Rm, we can write the corresponding density as follows:
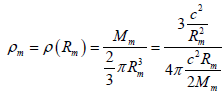 (6)
(6)
If we accept that the gravitational constant may be expressed by the following identity
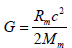 (7)
(7)
We can write relation (6) as follows:
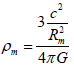 (8)
(8)
Obviously, position (7) is equivalent to identifying the amplitude of the harmonic motion with the Schwarzschild radius related to a mass equal to Mm.
If we consider the evolution of the Universe as an isentropic process, we may write the following, well known relation:
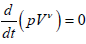 (9)
(9)
P represents the pressure, V the volume, and v a coefficient (commonly defined, in thermodynamics, as heat capacity ratio) that exclusively depends on the medium we are considering. According to Zeldovich [2], the relation between pressure and density (the equation of state) may be expressed as follows:
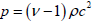 (10)
(10)
From relation (9), using the equation of state, we immediately obtain:
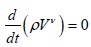 (11)
(11)
Among the various admissible value we can select
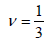 (12)
(12)
The previous position allows us to express relation (11) as follows:
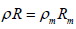 (13)
(13)
As a consequence, from equations (8) and (13) we may deduce:
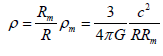 (14)
(14) 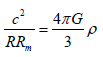 (15)
(15)
If we carry out the following position [3]
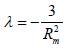 (16)
(16)
we may write relation (8) as follows:
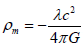 (17)
(17)
Now, from relations (3) and (4) we can immediately deduce:
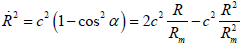 (18)
(18) 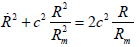 (19)
(19)
If the radius (R) is different from zero, considering the previous relation, using equation (15), we may write:
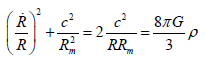 (20)
(20)
By using position (16), we may write relation (20) in the underlying form:
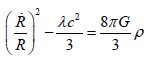 (21)
(21)
The previous relation represents the first Friedmann–Lemaître equation [4]. Naturally, λ coincides with the so called
cosmological constant. Equation (21) can be obviously written in the following form:
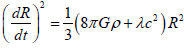 (22)
(22)
Equation (18) may be rearranged as follows:
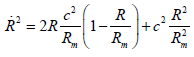 (23)
(23)
From the previous relation, by using equation (5) and position (16), we can deduce:
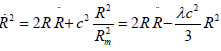 (24)
(24)
From the previous equation we can immediately obtain:
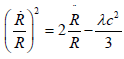 (25)
(25)
By using relation (10) and position (12) we may write:
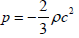 (26)
(26)
The previous identity allows us to write equation (21) as follows:
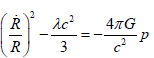 (27)
(27)
Multiplying by two the first and second member of the previous equation, we can easily obtain:
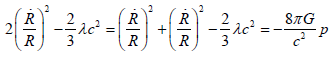 (28)
(28)
Finally, using relation (24), we can write the second Friedmann–Lemaître equation
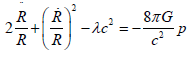 (29)
(29)
As suggested by the title, the purpose of this paper exclusively lies in deducing relations (21) and (28) without using Einstein's equations [5]. Homogeneity and isotropy are taken for granted. Positions (7) and (12) are not discussed in this specific paper. Very roughly, the first of the above-mentioned positions suggests the idea that the Universe, in a certain sense and measure, could be imagined as a huge black hole (the amplitude of the harmonic motion coincides with the Schwarzschild radius). The second, carried out consistently with the current observations, is obviously related to the presumed existence of dark matter-energy. Although the issue is not considered in this paper, it is easy to understand that, if we accept the variation of distances as a real phenomenon, we are forced to take into consideration kinds of matter and energy that we cannot properly define as ordinary.