About Nature of Superconductivity and Superfluidity

The prevailing now BCS-theory is based on the phonon mechanism. The impetus for its development was the discovery of the isotope-effect in superconductors. As it has been observed, this effect (for some superconductors) has the same dependence on the mass of the isotope as the cut-off frequency of phonon spectrum.

It was found later that the zero-point oscillations of ions in the crystal lattice of metals are anharmonic. Therefore, the isotopic substitution leads to a change in the interatomic distances in the lattice, to a change in the density of the electron gas and hence to a change in the Fermi energy of the metal.

That was not known during the creation of the BCS-theory.

Conduction electrons in the metal are in a potential well. One must act photons or by heating, to pull them out from this well. The lowest level in the well is the level of zero-point oscillations. Quantum mechanics requires from particles at the lowest level to make these oscillations.

At a sufficiently low temperature, all bosons (i.e. electrons connected in pairs by some no matter specific mechanism) are collected at the lowest level and all have the same energy. That means that they have the same frequencies and amplitudes of zero-point oscillations.

But pairs of the same energy can have different phases and orientation (polarization) of the zero-point oscillations. If the temperature is not low enough (above the interaction energy of steam), the interaction between them can be neglected. At that the oscillating with different phases and polarizations pairs will be described by different wave functions. They are not identical.

Due to the fact that the charged particles oscillate, there is an interaction be- tween them. At sufficiently low temperatures, this interaction leads to a kind of ordered structure of zero-point oscillations at which due to their mutual attraction their energy decreases. As a result, this attraction forms a superconducting condensate, which is not scattered by the defects, if the scattering energy is less than the energy of attraction.

Calculations show that the ratio of the critical temperature of formation of such a condensate in I-kind superconductors to its Fermi temperature:

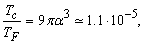(1)

(where α is the fine structure constant)

One more assumption must be made for II-kind superconductors, and then they, too, are well described by similar formula. High-temperature superconductors can be I-kind or II-kinds superconductors. These results are in good agreement with measurements (Figure 1).

Figure 1: The comparison of the calculated values of critical temperatures of superconductors with measurement data. Circles relate to type-I superconductors, squares show type-II superconductors.

The critical magnetic field in this model is a field that destroys the coherence of the zero-point oscillations of the particles of the condensate. This is also in good agreement with measurements (Figure 2). It is appropriate to emphasize that the BCS-theory there are no workable formula that determines the specific critical parameters of superconductors.

Figure 2: The comparison of the calculated energy of superconducting pairs in the critical magnetic field with the value of the superconducting gap.

A zero-point oscillation of shells of neutral atoms in the s-state was considered by Vasiliev [1]. He showed that the helium atoms arrange the oscillations of their shells at about 4K. This ordering is energetically favorable, since in this case the attraction arises between atoms. He paid no attention, that only one oscillation mode is ordered at this temperature. But this is enough for the helium liquefaction as repulsion is absent in the gas of neutral bosons. At a temperature which is 2 times less. The calculation shows that the temperature of complete ordering of zero-point oscillations depends on the universal constants only:

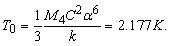(2)

This value agrees very well with the measured value of the superfluid transition temperature Tλ = 2.172K . This difference in the 4 digits may occur because of the inaccuracy of the calibration of thermometers, which are very difficult in this temperature range.

Also in this case it is possible to calculate the density of the superfluid condensate in liquid helium. It turns out that the density of particles in the condensate, as well as T0, depends on the ratio universal constants only:

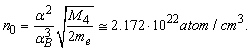(3)

(where B is the Bohr radius).

Since all helium atoms pass into condensate at a low temperature, then it is possible to calculate the density of the liquid helium:

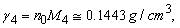(4)

which agrees well with the measured density of liquid helium equal to 0.145 g/cm³ .

It should be emphasized that the above formulas are derived from the consideration of the mechanism of zero-point oscillations ordering and they were not known previously.

Thus the consent of the above formulas with the measurement data clearly shows that both - superconductivity and superfluidity are the results of the work of the same mechanism - both of these related phenomena occur as a result of ordering zero-point oscillations.

References

1. Vasiliev BV. Superconductivity and Superfluidity, Science Publishing Group, NY 2015