Research & Reviews: Journal of Pure and Applied Physics
MenuISSN: 2320-2459
ISSN: 2320-2459
Moscow Institute of Physics and Technology, Department of Physics and Mathematics, Russia
Received Date: 15/05/2018; Accepted Date: 24/05/2018; Published Date: 31/05/2018
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
This paper considers the problem of the flat ring motion of a viscous capillary fluid rotating by inertia. As a result of numerical simulation of a viscous liquid ring oscillations have been detected. We describe the laws of the periodic motion of the considered system.
Fluid mechanics, Flat ring of viscous capillary fluid, Oscillations
This paper considers the problem of the flat ring motion of a viscous capillary fluid rotating by inertia, which corresponds to the description of the motion of an infinite rotating cylinder fluid in an environment without gravity. In practice, in the presence of some restrictions an analog of studied object may be section of vortex rings. These rings may be observed when gas or liquid flowing from the nozzle or in the turbulent layer formed by plane's wing air flow. In addition such objects as tornadoes, whirlpools in a cut shaped as vortex rings and if we go to the macroscopic scale we will find that some galaxies (called a ring galaxy) shaped like a ring. Therefore, the study of such objects does not lose its relevance.
The work describes the regularities of a periodic mode of movement of the ring of viscous capillary fluid without of the forces of gravity.
The basis of the plane problem statement of the liquid ring dynamics consists of Navier-Stokes equations. In vector form, this system has the form:
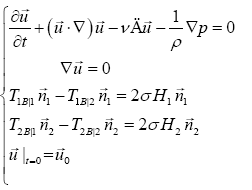(1)
where∇-Hamiltonian,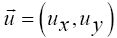 
: vector velocity field, t-time, ρ-density, p-pressure Δ-Laplace operator,ν-kinematic viscosity
coefficient, σ-surface tension coefficient, TiB|1-Cauchy stress tensor for liquid on i-th border, TiB|2-Cauchy stress tensor for gas
on i-th border, Hi-mean curvature on i-th border,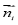 
normal on i-th ring border, i=1..2.
The stress tensor for classical Stokes fluid is used for describe the fluid dynamics.
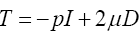(2)
Where P-hydrostatic pressure, I-identity tensor, μ-dynamic viscosity,
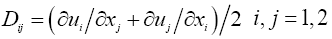-strain rate tensor
The stress tensor gas at the boundaries is:
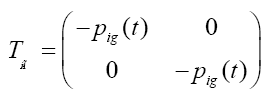(3)
Where Tij stress tensor of environment which in contact with liquid on i-th border, pig(t) - the variation law of gas pressure on i-th border.
Geometric formulation of the problem (Figure 1): Let r=R1(t), r=R2(t)-respectively the outer and inner boundary of the ring.
Figure 1: The geometry of the liquid ring
There R10, R20>0 and R10, R20-position of free boundaries in initial time.
Equations from system [1] were rewrited in polar coordinate system considering problem reflection symmetry. The sought-for
velocity vector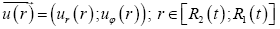 
depends on ring-point position only. Conversion to a new variable, which describe
a point on a ring in dimensionless form, occurs on the basis of next relations:
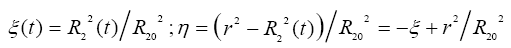(4)
Relations eqn. (4) changes value range of dimensionless spatial ring-point coordinate ηto time invariant line segment [0,a],
where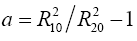 
note that η=0 corresponds to point position on internal ring border and η=a-on external.
Using the dimensionless procedure of time and unknown functions by the following formulas:
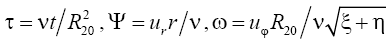-allowed to rewrite the system of eqn. (1) in the following form:
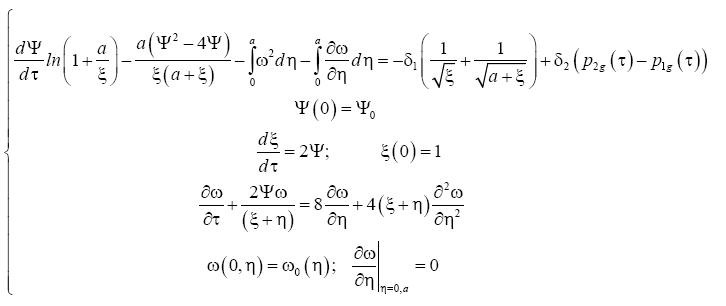(5)
where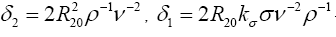 
-the combinations of the physical characteristics of the liquid and the geometric ring dimensions, in which kσ-the multiplier that takes into account the presence or absence of surface tension, which can be either
1 or 0 [2].
Previously the problem (5) has been intensively studied and have been described such motion modes as infinite expansion, the collapse of the ring and the stationary motion (motion as a rigid body) [3,4]. Note that problem (5) has no general analytical solution at the moment so the choice of a numerical method of its decision is well founded.
The numerical method we used was realized inside software "Ring v1.1" and was tested on single known at that moment solution [1]. In the next step series of numerical experiments with different system geometry and physical characteristics of the liquid and gas were made using this program. Movement of system liquid-gas as ring sizes (and linked with it pressure and velocity fields) dumping periodic oscillations were firstly found during numerical experiments. This behavior of the liquid ring was physically expected result, because the system includes the centrifugal force (or pressure differential) which tends to increase the ring sizes and the surface forces tending to reduce it. Figure 2 shows the results of numerical experiment using following input data: the physical characteristics of the water at room temperature for the liquid ring which is in the air; ring sizes are measured in centimeters-h=10-2m; initial dimensionless angular velocity, the initial dimensionless radial velocity Ψ(0) = 10. Quality factor of oscillation system reduce as 8 times as increasing viscosity as twice as high, thus energy lost as a result of dissipation reduced as 8 times as less.
Figure 2: Dependence of frequency and logarithmic decrement on the physical and geometric system
The periodic nature of the movement was observed for all functions describing the state of the dynamical system [5]. Moreover numerical simulations showed that the period of oscillation of the function Ψ, ξ, ω responsible for the state of the system is the same. It makes possible to select any from listed functions for analyze periodic motion mode. In this way associated with the description of ring size function ξ is the most illustrative in the author’s opinion.
Considering dynamic system described by a system of differential eqn. (5) it can be shown that this system has a stationary point of focus with coordinates and ξ* is solution of the following nonlinear equation:
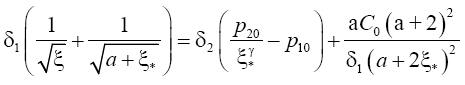(6)
where ω0=ω (0,η)=ω0(η)=C0=const. As a result of comparison found at the base [6] and the stationary value found on the basis of a numerical simulation for the same input parameters it was found that they are consistent with an error of about 1%. This means that the stationary state of a dynamical system can be found from formula (6) and confirms the validity of the numerical simulation.
The question about characteristics of the oscillatory process is raised due to the fact that detected oscillations were found as a result of numerical simulations. Therefore the transformation will continue by excluding function Ψ from the system [5] by assumption of smallness of rotate part from angular component (integrals from ω). As a result we get ordinary nonlinear differential equations of second order for required function ξ:
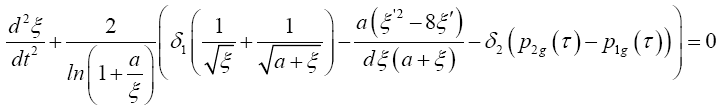(7)
The second term of this equation is a nonlinear function of the required function ξ(t) and its derivative ξ'(t) and the equation is not similar to the equation for the harmonic oscillator. For a detailed analysis of this equation we decompose the second term in the neighborhood of the stationary point by Taylor's formula and then using only linear approximation we obtain the equation of harmonic damped oscillations. Formula for the angular frequency and logarithmic decrement are obtained from the factors facing ξ and ξ'. The results of this procedure are shown in Table 1. Also given expressions for the intended generally, dependency, assuming that all the other parameters remain constant.
Table 1. Approximate formulas for engineering calculations.
| Description | Formula |
|---|---|
| The oscillation frequency of the dimensionless inner radius wx | 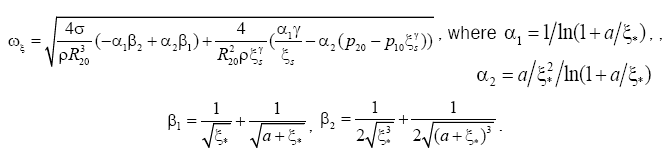 Noticed that ωξ independent of viscosity. |
| Logarithmic decrement of oscillations of the dimensionless inner radius δx |  |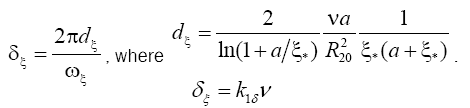
Such transformation of the original system [5] can be done also for the values Ψ(τ) and ω (τ,η). In particular from the formula
for the oscillation frequency follows that oscillation's frequency does not depend on the coefficient of dynamic viscosity (v) in a
first approximation and its magnitude is directly proportional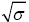 
inversely proportional 
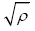and 
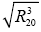moreover it is a complex
function of dimensionless ring width a
Logarithmic decrement was directly proportional to the dynamic viscosity coefficient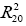 
and inversely proportional .
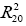Approximate formulas reliability was confirmed by numerical simulations. Figure 2 shows a comparison between results of numerical experiments and the obtained analytical dependences (dots show the values of the frequency and logarithmic decrement found from numerical experiments, straight lines - the approximation of the analytical results). Noticeably good agreement confirming the linear dependence of the angular frequency of the physical characteristics of the fluid according to the results shown in Table 1.
The behavior of other functions ψ(τ),ω(τ,η) that describe the dynamics of the ring is similar in nature. Moreover we cannot assert that the frequency of the periodic variations of these values coincide with ξ(τ). What does the second equation form (5). A detailed study of the nature of their changes will be of a similar character.
We note that all numerical experiments were calculated for liquid-gas systems with a Reynolds number varied in a range Re~1..1000. To analyze the behavior of these systems with other Reynolds numbers additional research is required.
It is shown that the results of numerical modeling of the system of eqn. (5) allow obtaining correct information about the nature of the behavior of the liquid ring in time (by comparing types of dependencies predicted by the theory and the resulting numerical simulation).
It describes a possible way of motion of the system as a liquid ring to a stationary state on the basis of periodic processes. According system [5] we obtain nonlinear oscillation equation for the relative ring's size [7] and approximate analytical relationship (Table 1) which describes the variation of frequency on size and physical characteristics of the liquid and gas.
Note that possibility of estimate periodic motion characteristics of vortex rings arising in different processes emit fluid and its flow obstacles based on the data of their geometry and physical environment characteristics is appeared.