Research & Reviews: Research Journal of Biology
MenuISSN: 2322-0066
ISSN: 2322-0066
Samuel Bonaya Buya*
Department of Mathematics/Physics at Ngao girls, Secondary School, Kenya
Received date: 16/01/2018; Accepted date: 18/01/2018; Published date: 18/01/2018
Visit for more related articles at Research & Reviews: Research Journal of Biology
A simple NP complete proof of Goldbach’s conjecture is presented. The principal used in its proof is well known, that is, every odd prime number can be expressed as a sum of an even number and one. Thus we show that a there is P-complete method of deriving Goldbach conjecture and an NP complete method of verifying the conjecture. As a way of verifying the conjecture a method of extracting primes from a set of even number is used.
Simple proof of Goldbach’s conjecture; Number theory ; Proof of the P verses NP problem
Goldbach’s conjecture is one of the oldest and unresolved problems in number theory and mathematics in general. The original conjecture (sometimes called the “ternary” Goldbach conjecture states “at least every number greater that is greater than 2 is the sum of three primes.”Goldbach considered 1 to be a prime, a convention no longer considered. As re-examined by Euler, an equivalent form of the conjecture (called the “strong” or “binary” Goldbach conjecture asserts that all even positive integers greater than two can be expressed as the sum of two primes [1,2].
The conjecture was proposed on June 7th 1742 by Christian Goldbach in a letter he wrote to Leonard Euler.
The expression given for a given even number as a sum of two primes is called Goldbach partition of that number.
Definition
Prime numbers consists of an even prime number (2) and odd prime numbers.
All prime numbers are odd non-composite numbers with exception of 2.
Premise one
Every odd number greater than 1 is a sum of an even number and one.
Premise two
Every odd prime number is the sum of an even number and one
Premise three
Two even numbers add to another even number
Theorem (Goldbach’s strong conjecture) every even integer greater than 2 can be written as the sum of two primes
Proof
Consider an even number e related to two prime numbers p2 and p2 via a variable number x through the relationships below:
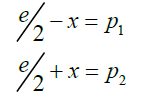(1)
For the above prime number conditions to be met the even number must be greater than 2.
On adding the two equations we obtain the mathematical expression of Goldbach conjecture given by:
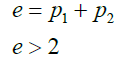(2)
In this case the solutions of the Goldbach conjecture are given by:
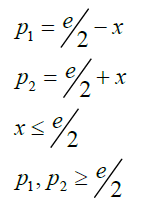(3)
Given therefore an even number e we can draw on the same axis the graphs of the equations 4 and identify the prime numbers that meet the condition 3.
Consider the even number e =2
The graphical solution is given as per (Figure 1) below:
Figure 1: pair of primes of e=2.
The primes are supposed to lie along the intervals AB and AC. Since e = 2, no such primes can be found.
Consider e = 12.
The solution of the pairs of primes that add to 12 can be obtained from the (Figure 2) graph below.
Figure 2: Pair of primes for e=12.
Here the solution is the primes at points A and D (5,7 ). Notice here that the triangle solution is getting bigger and therefore the likelihood of getting more than one pair of results is increasing (Figure 3).
Figure 3: Pair of primes for e=38.
Consider e = 38
Here the pairs of primes are (19,19), (31,7)
In general as the as the even number gets bigger, the isosceles triangle also gets bigger, and the more the likelihood of finding more pairs of solution. The triangle of depth 1 unit (representing e =2) does not have a pair of primes [3,4].
A computer program can be made for the pair of equations 4 to extract primes of any given even number. The primes themselves can be extracted as provided in the paper entitled “An algorithm for extracting primes”- By Samuel Bonaya Buya.
Thus a P and NP complete proof of Goldbach conjecture exists.
A proof of Goldbach conjecture has been achieved. A method does exist of extracting the pairs of primes of a given even number.