Research & Reviews: Journal of Pure and Applied Physics
MenuISSN: 2320-2459
ISSN: 2320-2459
Freelance Research Scientist, Bajkalsk 1170/28, Praha 10, Czech Republic.
Received Date: 28/10/2015; Accepted Date: 28/03/2016; Published Date: 30/03/2016
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
It is shown that widely accepted opinion which says that Euclidean groups cannot be located in space because they are abstract groups, is incorrect. Euclidean groups are quite certain groups of operators in space and as the symmetry operations have its location di ering by fractions of the translation normal-izer of the group the group itself has also a certain location. We show, however that derivation of space groups with the use of factor systems indeed leads to groups which are not located while derivation with the use of systems of non-primitive translations leads to a set of groups di ering in location by a fraction of their Euclidean normalizer. Some examples of possible use are given.
Symmetry; Crystallographers; Translation normalizer; Euclidean space.
At the time when the rest volume of the last but rest edition of the International Tables for Crystallography (the one with blue cover) was published, the author has been asked to write a review on it. On a special arrangement with Mathematical reviews, he wrote some two pages and being enthusiastic about the wide range of knowledge presented, he gave the table a nickname "The Bible of Crystallographers" [1]. On the 16th International Congress in Beijing (1995) the author had a vigorous discussion with the editor of Vol. A, concerning the concept of group location in connection with just prepared Vol E Sub periodic groups [2]. It appeared that many crystallographers believe that space and generally Euclidean groups cannot be assigned a location because they are abstract groups. To emphasize the con ict, the author presented an analysis of group location at Prague Congress of IUCr [3] but without response, though he used rather provocative change of the nickname to "The Old Testament". Recently, the author found on Wikipedia, under the title The Bible of Crystallographers, the reference to a book:
Symmetry in crystallography (Understanding the International Tables) [4] by Paolo G. Radaelli, Inter-national Union of Crystallography, Oxford University Press, 2011. Neither this book nor IT A contain even a hint of group location. Though it does not diminish the value of these publications, especially for practising crystallographers, we still believe, that the simple theory of location should be included into these publications.
The author was, for a long time, not sure, how to interpret such trivial thing as the choice of origin in the International Tables
Vol. A. Well, if a physicist wants to describe the motion of a rigid body of nite size, he has to de ne two coordinate systems. First
he has to specify the coordinate system in space by choosing a point P (the origin) and the three coordinate axes which are axed.
Then he needs to specify the location of a certain point P‘ within the body (for example, as usual, the centre of gravity of the body)
and also the coordinate axes in the body. Then you describe the motion of the body by the track of its origin P0 and by rotation
of its axes with reference to those of the coordinate system. Euclidean groups are represented by their diagrams which were so
nicely called the "symmetry pattern" by Prof. Wondratchek in Vol. A. It is assumed that the coordinate axes of the body (symmetry
pattern) in IT A are parallel with those of the space. Then you describe the location of the symmetry pattern by a vector from the origin P to P‘. In IT A the origin is specified by the sentence: Origin at (or in) point in a diagram of the group; as a rule it is the left
upper corner. We can assume, though it is nowhere explicitly said, that this is as well the origin of the coordinate system. This
assumption is not mandatory and the origin of the group may be on a distance s from the origin of coordinate system. This is well
known in cases of groups with two origin choices, where we can write for the group type P42/nmc=P42/nmc (origin 1) that the group P42/nmc(origin 2) equals the group P42/nmc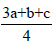
read the group P42/nmc shifted by 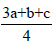This group is certainly
different from the group P42/nmc and hence its Hermann-Mauguin symbol contains also the shift. We can argue that it is the
same as if we write (origin 2) but the current notation can be used for any shift and it shows that the space group (generally each
Euclidean group) has a location, so that the Hermann-Mauguin symbol is not unique. It is unique up to a shift in the fundamental
region of the group translation normalizer. We have used such symbols in Vol. E of the International Tables; for example: for the group No 64, where the layer group p4/nmm(Origin 2) is denoted p4/nmm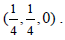
The conditions for a space group to be a subgroup of another space group are rather severe. However, the relations between groups are given for the group types which means in terms of Hermann-Mauguin symbols. The actual groups are then deduced by adding to these symbols their parameters, i.e. orientation of point groups, with information about screw axes and glide planes and orientation, Bravais types and metric parameters of their translation subgroups. If Hermann-Mauguin symbols with these data will de ne one certain group, then the relations between these symbols will be valid for all specific groups. The problem is that this information does not provide a unique group but still an in nite set of groups with a different location.
In all editions of Vol A of the International Tables maximal non-isomorphic subgroups (type I, IIa and IIb), maximal isomorphic
subgroups of lowest index (IIc) and minimal non-isomorphic super groups (I and II) are listed just in terms of Hermann-Mauguin
symbols. The location of groups is, however, completely ignored because most of crystallographers refuse to accept the concept
of group location. "How can we locate such an abstract object as a group?" is a question which the author had to face many times.
It would be certainly rather strange to accept location for an abstract group. However, space groups in this context and in Vol. A
are far from being abstract. They are operators on an Euclidean space and a shift of space by s moves an Euclidean group G to
a group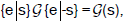
, where the last symbol means the group G shifted in space by s and this shift may take values in the
fundamental region of the group translation normalizer. We can de ne certain location of the group as the standard, assign the
Hermann-Mauguin symbol to it and write the shift s behind this symbol. Hence there is a continuous set of groups with different
locations but only one of them is the subgroup of the original group. We shall now explain the use of the location on an example.
Thus, in the left hand side of Figure 1a we have the diagram of the group p4/nbm (origin 1) while the second diagram of the
same group, Figure 1b in another location (origin 2) on the right is denoted by p4/nbm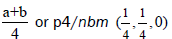 
where origin 1.
Means the origin of the space coordinates, while origin. 2. Denoted the original group moved by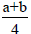 
There is further the diagram
of the group P 422 in red which is the diagram of that group of this type which is the subgroup of the group p4/nbm, while neither
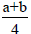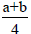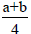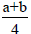the diagram of nor P422 that of P4212 may correspond to a subgroup of p4/nbm However, if we move the group P422 by , we get a group P422 which is a subgroup of the group p4/nbm The criterion for being a subgroup according
to diagrams is easy - the diagram of the subgroup must overlap with the diagram of the super group; we suggest using the term
"location compatibility". Such group as P4212 cannot be a subgroup of the group p4/nbm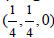 
simply because its Hermann-
Mauguin symbol contains the glide axis 21 which is not in the group P422 because it is not location compatible.
Figure 1: Continuous set of groups with different locations but only one of them is the subgroup of the original group.
It follows that neither the equi translational subgroups listed by Neubuser and Wondratchek [5] nor the equi-class subgroups
by Boyle and Lawrenson [6,7], nor the numerous issues of Vol. A. of the International Tables Vol. A (4) give exact information
about the subgroups. Such information is only partial. The Hermann-Mauguin symbols which are considered a SACRED COW
by crystallographers are also actually not unique: To one symbol 
there corresponds a set of groups (s) with s from the
fundamental region of its translation normalizer. The symbol (Origin 2) actually means (s) is the shift of Origin 2 from Origin
1. This notation is so far used only in Vol E of the International Tables 2002 and further editions).
The diagram of the group P422 is location compatible with the diagram od the group p4/nbm (overlaps it and is its subgroup) (Figure 1a).
Neither of the diagrams of groups P422 and P4212overlaps with that of the group p4/nbm 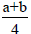, , but the diagram of the
group P422 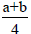does (Figure 1b).
We shall now consider four diagrams of space groups. The First two figures are the diagrams of the group No 125 p4/nbm at origin choice 1 (1a) and at the origin 2 (1b), next is the diagram of the group No 89 P222 (2) and the diagram of the group No
90 P2212 (3). These diagrams show the symmetry elements of these groups in the unit cell at the plane ab, origin at the left upper
corner. If we put the diagram (2) over the diagram (1a) we see, than all the symmetry elements on (2) coincide with the elements
on the diagram (1a). The groups are location compatible. The group P222 cannot be therefore a subgroup of p4/nbm, but if we
shift it by 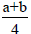,it does.
To each group in IT A there is given a list of representative symmetry operations. Instead of rather obsolete and clumsy
notation in IT A we list these operators by Seitz symbols. Such a symbol has the form {g u(g)}P , where g is the element of the
point group and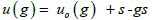 
where uo(g) is the screw or gliding translation and P+s is the location of the element. In
the Table below, these symmetry operations are listed for the group p4/nbm, p4/nbm 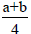, P422 and P4212. The symmetry
operations of the group p4/nbm are the same as for the group P422 and hence the latter group is a subgroup of the former.
For the group p4/nbm 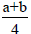we first express the Seitz symbols with reference to the point 
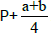We need, however, to
compare the operations with reference to the same point P.
It is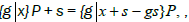 
called the shift function, we can read these symbol either from the diagram or transforming
those with reference to P (Table 1).
Table 1: Comparing the systems of non-primitive translations.
Comparing the systems of non-primitive translations we see, that the group P422 is a subgroup of the group p4/nbm
because their Seitz symbols are identical for each Figure 2. We shall call this property location compatibility. Actually the groups
are location compatible, if three independent Seitz symbols are locally compatible. Neither the group P422 nor the group P4212
are even locally compatible with the group p4/nbm 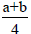and hence cannot be its subgroups. However, the group P422 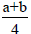is
locally compatible with the group p4/nbm 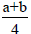and hence it is its subgroup.
Figure 2: Two domains from a phase transition to a halving equi translational subgroup.
Quite generally: If a group H is a subgroup of the group , then the group H(s) is a subgroup of (s) and vice versa.
There are two algebraic approaches to the development and systematic of space groups:
1. Theory of group extensions [8].
2. Theory of the sets of non-primitive translations [9].
1. Finding the extension of the group Τ by the group G or solving the short exact sequence 0→Τ→→G means in algebra
that of ending the group , which has a normal subgroup Τ such, that the quotient group /Τ is isomorphic with the group G. This
is a typical problem of ending the space group with translation subgroup and a point group G.
Without going to intricacies of the cohomology theory we know the result. The pair (G; Τ) called the arithmetic class, where G acts as automorphisms of the group Τ (in other words, the group G is a group of operators on T), induces a set of groups G(α) which belong to this class. Each of these groups is defined by a "factor system" m T and there is a nite number of different groups G (α) this property. All the groups G(α) thus defined are abstract groups because their derivation uses only the abstract groups. The factor systems m (α) (g, h) Cohomology group whose order equals the number of algebraically different groups G (α) of the geometric class (G, Τ).
2. In the next method we begin with the decomposition of the group G into cosets of its subgroup T. We use the fundamental
theorem on Euclidean groups which says that each Euclidean group can be uniquely expressed as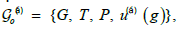 
Where G is the point group, T its G-invariant translation subgroup, P the origin of coordinate system and u( α)(g) the so-called system of non-primitive translations, which satisfies so-called Frobenius congruences
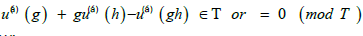
Where
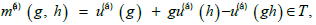
is the factor system. If we add the function t(g) + gt(h) t(gh) to a given system of non-primitive translations, the resulting function will be again the system of non-primitive translations leading to the same factor system, so that we can restrict the function u()(g) to values in the unit cell of T. Such Systems of non-primitive translations are called normalized.
The proof of the theorem is rather easy. We perform the coset resolution of the group G of the translation subgroup T :
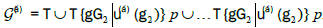
Multiplication of elements from two cosets then gives:
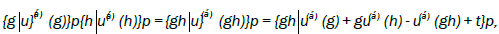
which leads to Frobenius congruences.
Systems of non-primitive translations have the property, that the sum of two systems is again the system of non-primitive translations because it also satisfies Frobenius congruence and the shift function φ(g; s) is also a system of non-primitive translations, because
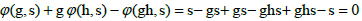
The shift by bms leads to the group
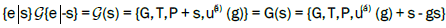
Which is the group G shifted in space by s?
The set of the systems of non-primitive translations u(α)(g) + s - gs is therefore an abelian group U and the set of the of shifts φ(g; s). All groups of arithmetic class (G; T) are expressed by and the set of shifts φ(g; s) is a group G (bms), where distinguishes n group types and s the vectors of the fundamental region of the translation normalizer ΤN(G) which is identical for all groups of the arithmetic class. These are the actual groups which are listed in Vol A or Vol E.
Let us note that equi translational subgroups of space group with respective shifts are given already in [10] and that all previous data in Vol. A are also completed by shifts in [11]. Unfortunately, the last publication though it provides very valuable information about relations among space groups interprets the shifts as the shifts of the origins but not of subgroups.
Examples of possible use
Practical crystallographers are usually influenced by the fact, that they are analyzing single crystals. But there exists undoubtedly crystal structures, which contain two or more monocrystals, like domains, twins and we shall make even some modest attempt at in commensuration [12-14].
1. Antiphase domains. In Figure 2, we have two domains from a phase transition to a halving equi translational subgroup. There will appear two domains of different structures. As an example we consider the case when in one domain atoms are moved in one direction with reference to original structure, in the other they are moved in the other directions. The domains will have the same symmetry G but it will not be necessarily the same groups - they may well differ in their location. This will be clear if we perform the scanning for layer groups. These may follow even in different positions in the individual domains
Than the positions, predicted by scanning theory for homogeneous crystal. The boundary between the two domains will therefore interrupt the homogeneity, the structure corresponding to layer groups may fade in the direction to the centre, losing some atoms and respective symmetry elements (a process which can be named symmetry dilution, till, in the centre, there will remain only trivial layer symmetry. We do not use here the term plane symmetry, because it is the symmetry of two dimensional objects in two dimensional spaces while trivial layer symmetry is two dimensional symmetry in three dimensions. Holser (11) uses the term symmetry of a two sided plane which is actually an oxymoron, because all planes in three dimensions have two sides, and the groups he has in mind are now standardly called the layer groups. The trivial layer groups are not the plane group; the difference is also emphasized by symbols and names in Vol. A. as compared with Vol.E. In chapter 4.2 by Bertaut in Vol. A are used the names for symmetry elements: rotation points and ordinary or glide lines.
2. Lamellar twins. Again we have two components in the left and right twins, generally with different symmetries. The respective groups may now differ not only in their location but also in their orientation. Again we assume different scanning from left and right. In the middle there will again remain a region with at symmetry of some of the trivial layer groups (Figure 2).
In Figure 3, we illustrate the twin of symmetry p4/nbm with z-axis horizontal. You may now consult Vol. E, pages 348, 485 and 336. We consider the scanning direction (001) where the group p4/bnm is also the scanning group. There are the layer groups p/4bn of two orbits on distances d/2 - different orbits means that though the layer groups are identical, their environments are different (their location differ by half of unit cell in this direction not by the cell size. Between layer groups we have the symmetry p/4bm of trivial layer group where the structures also belong to two orbits, depending on the layer group in vicinity. Now we assume that towards the centre, the layer groups lose some of their symmetry elements till there remain only the elements of the trivial layer group p4bm in the canter. The distances on which the distorted layer groups as well as the resulting central group appear may be of several d which makes the model plausible.
Figure 3: The twin of symmetry p4/nbm with z-axis horizontal.
These two hypothetical cases may be experimentally verified. If we cut a thin plate in the canter of this arrangement, the plate will allow properties which will not be allowed in the bulk. Theoretically, all properties which are allowed by trivial layer or magnetic layer groups may be exhibited.
Notice again, that we use the term trivial layer groups, not the plane groups.
3. This case is highly hypothetical. Let us assume regular arrangements of the units of a group G. A unit with slightly higher
length of unit cell in a certain direction may be described as (d), the next by (2 d),..... (nd), up to a maximum of n and
then diminish the cell back. If n is irrational, we obtain some structure which can be called "incommensurate" (Figure 4); such
incommensurability may appear in three independent directions. Maybe this is rather naive, but such structures really appear in the nature. If you travel by plane and your take o is directed toward the sea, you can observe a set of ridges on the surface, which
is, how you see the set of waves. After the plane height rises, these ridges will vanish but another increase in height leads to the
appearance of new ridges, which evidently correspond to the waves of bigger wavelength (Figure 5). If you are lucky, the wider
waves will appear while the narrower are still recognizable then you will see a special wave structure.
Figure 4: The units of a group G. A unit with slightly higher length of unit cell.
Figure 5: The wider waves will appear while the narrower are still recognizable.
The whole problem with group location is in the small region in which the location can change. It is even a fraction, about one half, of the size of unit cell and hence the justification may appear only in very exact experiments, if it is not a crazy dream. The width of the central region may be however much bigger than d which makes the model plausible. The author is neither specialized neither in twin theory nor experienced with in commensurate states. However, he thinks that the location of groups should be at least recognized in such publications as the International Tables of Crystallography. The systems of non-primitive translations are given for classical groups in a book on crystallography in higher dimensions [15].
The author expresses his sincere thanks to Prof. Prochazka for the nice lectures of cohomology he gave us years back, as to Prof. Litvin and Janovec for discussions and encouragement.