ISSN: 2320-2459
ISSN: 2320-2459
Department of Physics, Centre for Research in String Theory, Queen Mary University of London, Mile End Road, London, E1 4NS, UK.
Received date: 06/05/2015; Accepted date: 04/03/2016; Published date: 30/03/2016
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
We generalise the study of constraints imposed by supersymmetry on the Berry connection to transformations with component elds in representations of an internal symmetry group G. Since the elds act as co-ordinates of the underlying space one nds a non-trivial extension to its structure and, correspondingly, there are new non-abelian constraints on the Berry connection. The speci c case of G = SU(2) is shown to constrain the connection to behave as a magnetic monopole over su(2), its Lie algebra.
The notion of a Berry Phase is that of a path-dependent U(N) holonomy of a quantum system under adiabatic changes of external parameters [1,2]. Hence, as one adiabatically varies a set of parameters Φn around a closed path, degenerate states |a> in the quantum system undergo a holonomy.
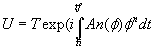 (2.1)
(2.1)
Where 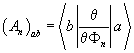 is the connection over the space of parameters [3]. Berry connections have been subject of much interest [4-8]. In particular, by considering super symmetric quantum mechanical systems, one finds that this connection must obey specific differential equations and is thus computable even when energy Eigen states of the parameters are unknown. In [4] by demanding the most general matrix-valued Lagrangian with an explicit connection term be invariant under vector multiplet super symmetry transformations, the authors found that the connection must obey the Bogomolny Monopole equations. Similarly, when one uses chiral multiplet parameters, the connection is found to obey the tt* equations [4,5]. These conditions were later generalized in [8] where the connection was found to obey the self-dual Instanton equations, from which the previous results are obtainable via dimensional reduction. Within String theory, Berry phases have been studied arising from particular brane constructions [9,10].
is the connection over the space of parameters [3]. Berry connections have been subject of much interest [4-8]. In particular, by considering super symmetric quantum mechanical systems, one finds that this connection must obey specific differential equations and is thus computable even when energy Eigen states of the parameters are unknown. In [4] by demanding the most general matrix-valued Lagrangian with an explicit connection term be invariant under vector multiplet super symmetry transformations, the authors found that the connection must obey the Bogomolny Monopole equations. Similarly, when one uses chiral multiplet parameters, the connection is found to obey the tt* equations [4,5]. These conditions were later generalized in [8] where the connection was found to obey the self-dual Instanton equations, from which the previous results are obtainable via dimensional reduction. Within String theory, Berry phases have been studied arising from particular brane constructions [9,10].
In this paper we investigate the constraints on the Berry connection which result from super symmetry transformations with component fields in representations of an internal symmetry group G. This is a natural non-abelian extension of [8]. In section 2 we construct the most general Lagrangian, to quadratic order, built from these fields. The underlying space on which the theory lives acquires a new structure and, correspondingly, in section 3 we nd interesting new constraints, imposed by super symmetry, on its connection. As a specific example the simplifying choice G = su(2) is shown to constrain it to exist as a mixture of a self-dual instanton and a monopole solution over 
 su(2)
su(2)
We are interested in applying super symmetry to a quantum mechanical Lagrangian with component fields in representations of an internal symmetry group. We focus on the case where the bosonic components of the super multiplet act as coordinates over the space S on which the theory exists. In this case, the connection is simply a leading order term in the Lagrangian.
In [4] the bosonic fields Φμ act as coordinates for an underlying 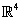 manifold. When these fields are promoted to exist in representations of an internal symmetry group, this manifold acquires a new structure. The fields now parametrize
manifold. When these fields are promoted to exist in representations of an internal symmetry group, this manifold acquires a new structure. The fields now parametrize
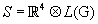 (2.2)
(2.2)
Where 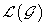 denotes the Lie algebra of the internal group G. This space is spanned by the bosonic coordinate’s Φμ, with Greek indices denoting the
denotes the Lie algebra of the internal group G. This space is spanned by the bosonic coordinate’s Φμ, with Greek indices denoting the 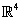 ,and lower case roman alphabet indices spanning
,and lower case roman alphabet indices spanning 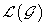 .We will see that super symmetry imposes non-trivial constraints on its connection.
.We will see that super symmetry imposes non-trivial constraints on its connection.
Consider the following super symmetry transformations1
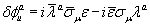 (2.3)
(2.3)
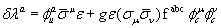 (2.4)
(2.4)
Where 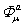 are the components of a real bosonic field, λa are two-component complex fermionic components, is a twocomponent super symmetry generator, fabc are the structure constants of an internal symmetry group generated by
are the components of a real bosonic field, λa are two-component complex fermionic components, is a twocomponent super symmetry generator, fabc are the structure constants of an internal symmetry group generated by 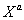 and g its corresponding coupling strength. This is the non-abelian extension of the transformations presented in [8]. We assign engineering dimensions to these parameters consistent with the super symmetry transformations:
and g its corresponding coupling strength. This is the non-abelian extension of the transformations presented in [8]. We assign engineering dimensions to these parameters consistent with the super symmetry transformations: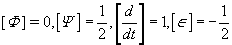 and [g] = 1. With these assignments we construct a super-symmetric Lagrangian with a connection term linear in time derivatives. The most general form this can take is
and [g] = 1. With these assignments we construct a super-symmetric Lagrangian with a connection term linear in time derivatives. The most general form this can take is
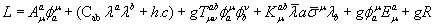 (2.5)
(2.5)
Where 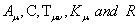 are functions of
are functions of 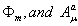 is the connection. In the above h.c denotes hermitian conjugation.
is the connection. In the above h.c denotes hermitian conjugation.
A. Scalar-Valued Lagrangian
We now demand 2.5 are invariant, up to a total derivative, under the transformations 2.3 and 2.4.
One finds that if,
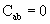 (2.6)
(2.6)
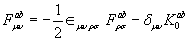 (2.7)
(2.7)
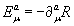 (2.8)
(2.8)
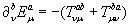 (2.9)
(2.9)
and,
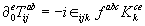 (2.10)
(2.10)
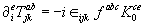 (2.11)
(2.11)
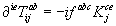 (2.12)
(2.12)
Where θ is a matrix valued function of the parameters appearing in the Lagrangian and crucially the commutator here runs over the promoted algebra of the function coefficients, not over the internal symmetry group. Demanding the new Lagrangian be invariant under 2.3 and 2.4 one finds results similar to the scalar-valued case discussed previously with = and the replacements of ordinary derivatives with covariant ones:
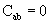 (2.14)
(2.14)
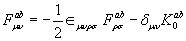 (2.15)
(2.15)
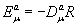 (2.16)
(2.16)
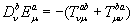 (2.17)
(2.17)
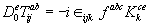 (2.18)
(2.18)
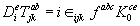 (2.19)
(2.19)
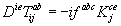 (2.20)
(2.20)
And the indices i; j indicate the = 1; 2; 3 components. Note that the extra structure of the underlying space means that this field strength is different to that commonly known: for example Fμμab ≠ 0
B. Matrix-Valued LagrangianIn this section we promote all functions multiplying multiplet field components in 2.5 to matrices in U(N). As the functions in the Lagrangian are matrix valued, invariance under super symmetry requires that [11]
Where 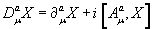 and now
and now 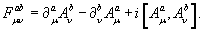 The commutator appearing here are strictly over the U(N) promoted matrix structure of the Lagrangian, not over the internal group G.
The commutator appearing here are strictly over the U(N) promoted matrix structure of the Lagrangian, not over the internal group G.
Crucially, in the limit g → 0, where the transformations reduce to n copies of the abelian internal group and the new g-dependent factors in the Lagrangian dis-appear, one recovers the results of [8] with 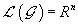
We wish to investigate the constraints posed by super symmetry on the connection. These constraints have a novel non-abelian contribution coming from the non-trivial internal symmetry group of the multiple components. These contributions are most apparent from 2.19 and the eld strength equation 2.15.
Combining these in general gives an equation of the form
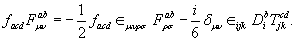 (3.21)
(3.21)
Then, for μ≠ν we have
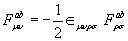 (3.22)
(3.22)
Which, at least for the case of a = b, we recognise as dim (G) copies of an instanton constraint over 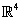 . For μ=ν one has (we have deliberately avoided to include the double index).
. For μ=ν one has (we have deliberately avoided to include the double index).
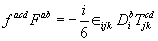 (3.23)
(3.23)
Which is a novel constraint on the connection over the new structure L (G) of the underlying manifold.
A. The simplifying case of 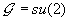 .
.
General solutions of 3.23 are hard to find, however one can make a simplifying ansatz to uncover a particularly simple solution. We take the internal symmetry group to be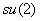 then
then 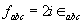 and
and 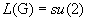 , so that 3.23 becomes (after contraction over a pair of indices).
, so that 3.23 becomes (after contraction over a pair of indices).
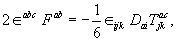 (3.24)
(3.24)
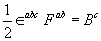 (3.25)
(3.25)
Where 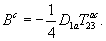 Together with 3.22, this means that the connection behaves as a generalisation of a U(N)
Together with 3.22, this means that the connection behaves as a generalisation of a U(N)
Instanton over 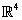 and, provided
and, provided 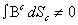 for a chosen surface
for a chosen surface 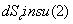 , it describes a magnetic monopole in
, it describes a magnetic monopole in 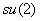 .
.
In this paper we have shown that imposing super symmetry with component fields in representations of an internal symmetry group G to the most general quantum mechanical Lagrangian built from such fields (with an explicit connection term) results in non-trivial novel constraints on the Berry connection. The underlying manifold acquires a new structure 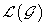 corresponding to the Lie algebra of the internal group. Whilst on the original
corresponding to the Lie algebra of the internal group. Whilst on the original 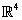 the connection is always constrained to obey the self-dual instanton equations, it is on this new structure that the new features are observed. In the simplest case, where
the connection is always constrained to obey the self-dual instanton equations, it is on this new structure that the new features are observed. In the simplest case, where 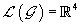 and the chosen group is abelian one recovers the results of [8]. Furthermore, in the simplifying case of G = su(2) the new constraints are shown to be those of a monopole over su(2) . In general, 3.23 is a novel constraint on the Berry connection overL (G) . It would be interesting to investigate whether a different choice for G also gives a known solution for the Berry Connection. We leave this for further work.
and the chosen group is abelian one recovers the results of [8]. Furthermore, in the simplifying case of G = su(2) the new constraints are shown to be those of a monopole over su(2) . In general, 3.23 is a novel constraint on the Berry connection overL (G) . It would be interesting to investigate whether a different choice for G also gives a known solution for the Berry Connection. We leave this for further work.
In [12,13], similar constraints on a su(2) connection were found by a harmonic super space approach. An explicit form for the super eld action was given for the case where the underlying manifold is 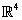 In our case, where the manifold becomes
In our case, where the manifold becomes 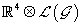 we expect a similar argument to hold, even though no explicit action was given here. This has interesting connections to string theory, from which this general construction is thought to exist in a low-dimensional limit or a particular brane construction.
we expect a similar argument to hold, even though no explicit action was given here. This has interesting connections to string theory, from which this general construction is thought to exist in a low-dimensional limit or a particular brane construction.
The author would like to thank D. Tong and D.R. Gomez for providing essential insight into this work and is also grateful to D.S. Berman and D. Thompson for useful discussions. GT is supported by an EPSRC grant.