1Faculty of Science, Alexandria University, Egypt
2Faculty of Science, Damanhour University, Egypt
Received date: 21/01/2016; Accepted date: 14/04/2016; Published date: 18/04/2016
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In this paper we are concerned with a nonlocal problem of a stochastic differential equation that contains a Brownian motion. The solution contains both of mean square Riemann and mean square Riemann-Steltjes integrals, so we study an existence theorem for unique mean square continuous solution and its continuous dependence of the random data X0 and the (non-random data) coefficients of the nonlocal condition ak. Also, a stochastic differential equation with the integral condition will be considered.
Integral condition, Brownian motion, Unique mean Square solution, Continuous dependence, Random data, Non- Random data, Integral condition
Many authors in the last decades studied nonlocal problems of ordinary differential equations, the reader is referred to [1-7], and references therein. Also the theory of stochastic differential equations, random fixed point theory, existence of solutions of stochastic differential equations by using successive approximation method and properties of these solutions have been extensively studied by several authors, especially those contain the Brownian motion as a formal derivative of the Gausian white noise, the Brownian motion W (t), t ∈ R, is defined as a stochastic process such that
W (0) = 0; E(W (t)) = 0, E(W (t))2 = t
and [W (t1) W (t2)] is a Gaussian random variable for all t1, t2 ∈ R. The reader is referred to [8,9] and [10-16] and references therein.
Here we are concerned with the stochastic differential equation
dX(t) = f (t, X(t))dt + g(t)dW (t), t ∈ (0, T ] (1)
with the nonlocal random initial condition
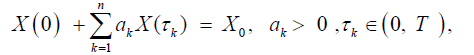 (2)
(2)
where X0 is a second order random variable independent of the Brownian motion W (t) and ak are positive real integers. The existence of a unique mean square solution will be studied. The continuous dependence on the random data X0 and the nonrandom data ak will be established. The problem (1) with the integral condition will be considered.
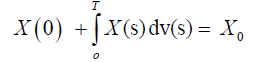 (3)
(3)
Let C = C(I, L2( Ω)) be the class of all mean square continuous second order stochastic process with the norm
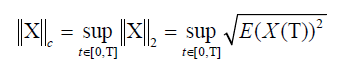
Throughout the paper we assume that the following assumptions hold
(H1) The function 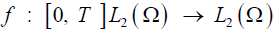 is mean square continuous.
is mean square continuous.
(H2) There exists an integrable function k : [0, T ] → R+ , where
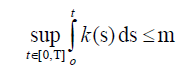
such that the function f satisfies the mean square Lipschitz condition
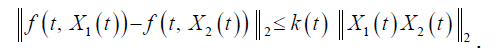
(H3) There exists a positive real number m1 such that
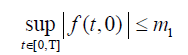
Now we have the following lemmas.
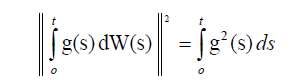
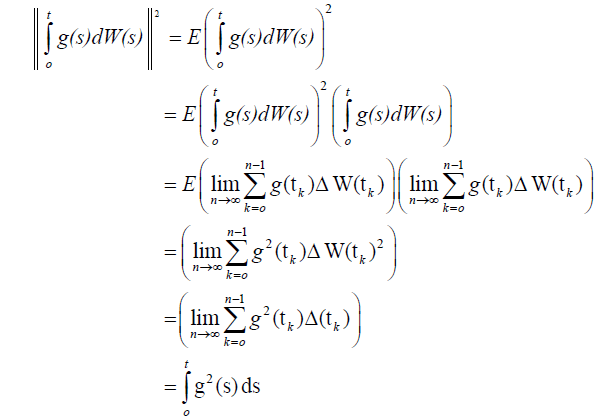
This completes the proof.
Lemma 2.2: The solution of the problem (1) and (2) can be expressed by the integral equation
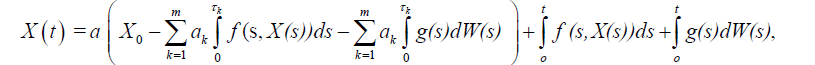 (4)
(4)
where
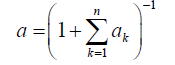
Proof. Integrating equation (1), we obtain
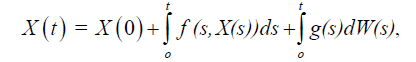
and
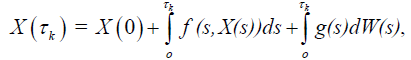
then
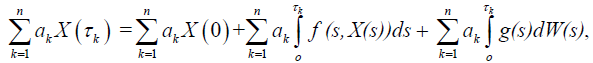
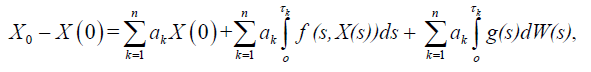
and
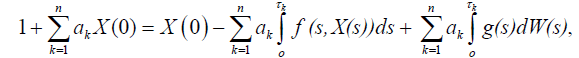
then
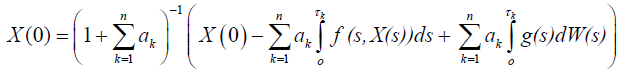
Hence
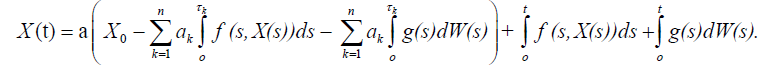
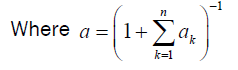
Now define the mapping
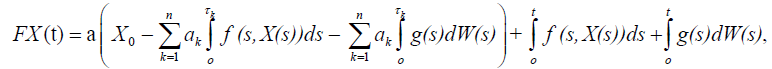
Then we can prove the following lemma.
Lemma 2.3 F : C → C.
Proof.Let 1 2 X ∈C, t , t ∈ [0, T] such that 2 1 t -t <δ , then
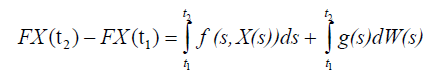
From assumption (ii) we have
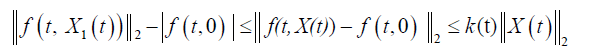
then we have
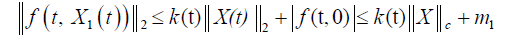
So,
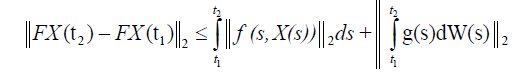
using assumptions and lemma 2.1, we get
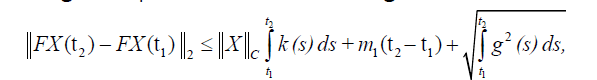
which proves that F : C → C.
For the existence of a unique continuous solution X ∈ C of the problem (1)-(2), we have the following theorem.
Theorem 3.1 Let the assumptions (H1)−(H3) be satisfied. If 2m < 1, then the problem(1)-(2) has a unique solution X ∈ C.
Proof. Let X and X* ∈ C, then
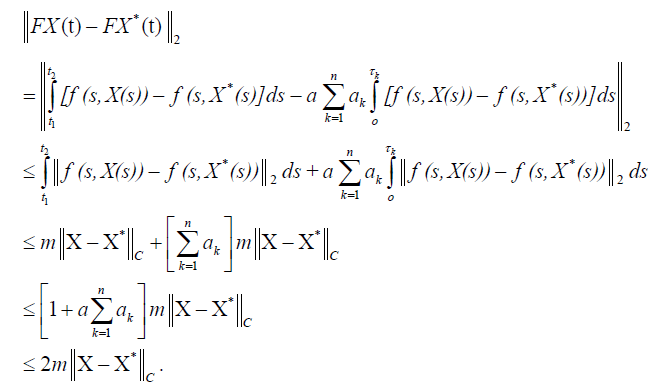
Hence
If 2m < 1 , then F is contraction and there exists a unique solution X ∈ C of the nonlocal stochastic problem (1)-(2), [2]. This solution is given by (4)
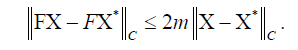
Consider the stochastic differential equation (1) with the nonlocal condition
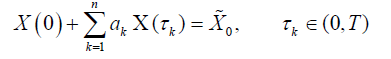
Definition 4.1 The solution X ∈ C of the nonlocal problem (1)-(2) is continuously dependent (on the data X0) if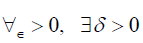 such that
such that 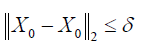 implies that
implies that 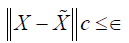
Here, we study the continuous dependence (on the random data X0) of the solution of the stochastic differential equation (1) and (2).
Theorem 4.2 Let the assumptions (H1) − (H3) be satisfied. Then the solution of the nonlocal problem (1)-(2) is continuously dependent on the random data X0.
Proof. Let
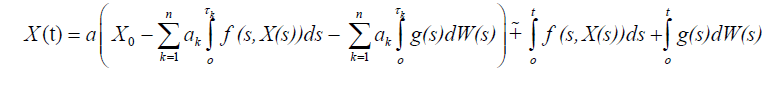
be the solution of the nonlocal problem (1)-(2) and
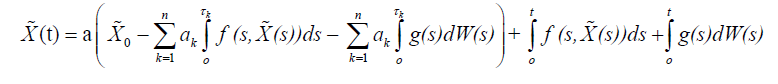
be the solution of the nonlocal problem (1) and (6). Then
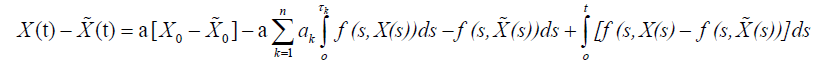
Using our assumptions, we get
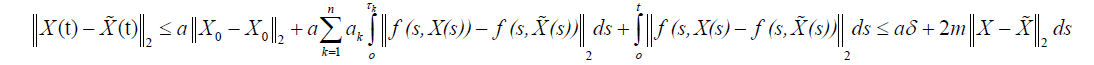
then
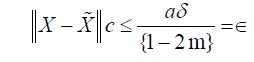
This completes the proof.
Now consider the stochastic differential equation (1) with the nonlocal condition
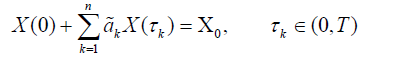
Definition 4.2 The solution X ∈ C of the nonlocal problem (1)-(2) is continuously dependent (on the coefficient ak of the nonlocal condition) if 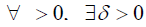 such that
such that 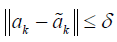 implies that
implies that 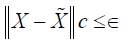
Here, we study the continuous dependence (on the random data X0) of the solution of the stochastic differential equation (1) and (2).
Theorem 4.3 Let the assumptions (H1) − (H3) be satisfied. Then the solution of the nonlocal problem (1)-(2) is continuously dependent on the coefficient ak of the nonlocal condition.
Proof. Let
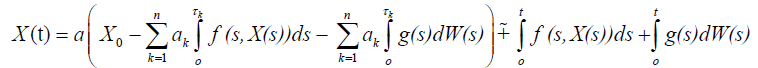
be the solution of the nonlocal problem (1)-(2) and
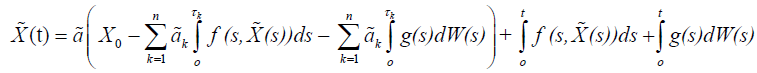
be the solution of the nonlocal problem (1) and (7). Then
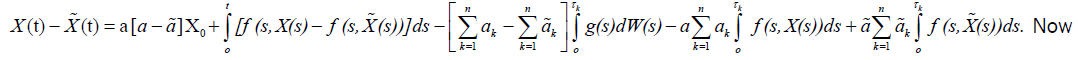
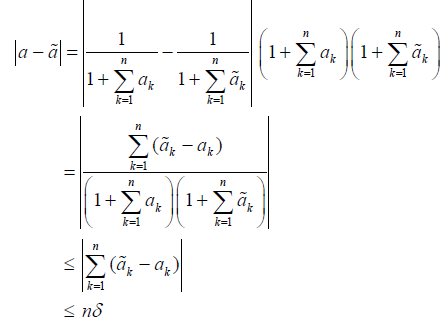
and
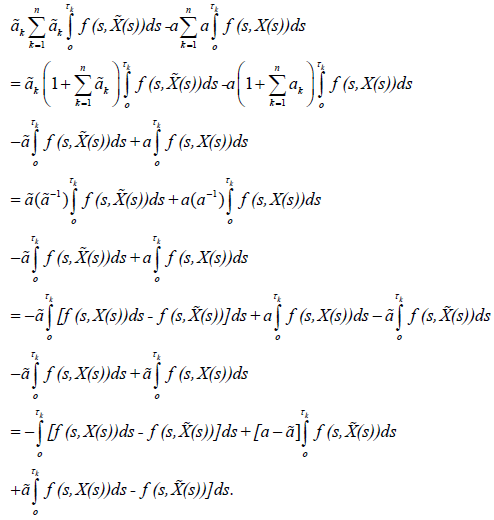
and
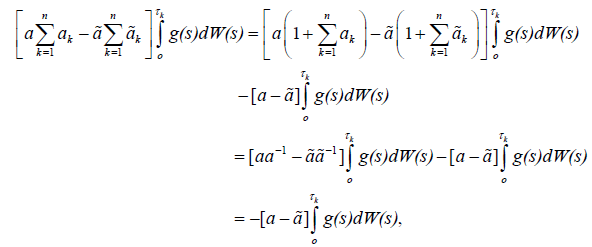
Then
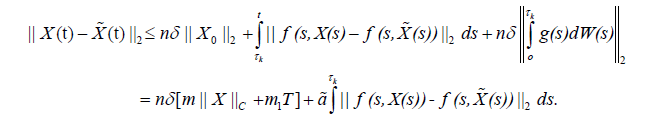
Using our assumptions we get
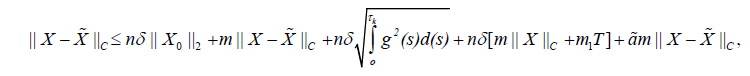
then
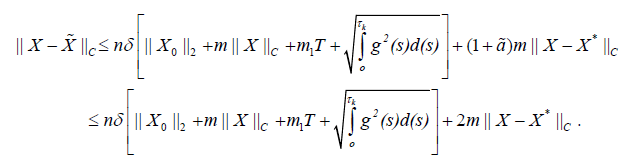
Hence
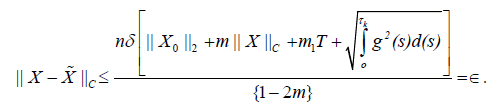
This completes the proof.
Let ak = v(tk) − v(tk −1), τk ∈ (tk−1, tk), where (0 < t1 < t2 < t3 < …< T).
Then, the nonlocal condition (2) will be in the form
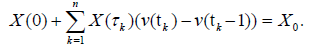
From the mean square continuity of the solution of the nonlocal problem (1)-(2), we obtain from [15]
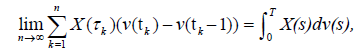
that is, the nonlocal conditions (2) is transformed to the mean square Riemann-Steltjes integral condition
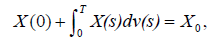
Now, we have the following theorem.
Theorem 5.4 Let the assumptions (H1)-(H3) be satisfied, then the stochastic differential equation (1) with the nonlocal integral condition (3) has a unique mean square continuous solution represented in the form
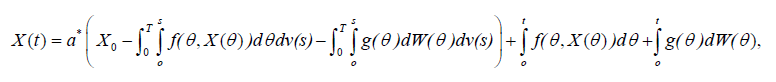
Proof. Taking the limit of equation (4) we get the proof.