ISSN: 2322-0066
ISSN: 2322-0066
Frederic BM1* Roger T2, Benoit N2 and Herve EB3
1Faculty of Science,University of Yaounde I,P.O. Box 812 Yaounde, Cameroon, France
2National Advanced School of Engineering of Yaounde, Cameroon, France
3Mekin Hydroelectric Development Corporation P.O. Box 13 155 Yaoundé, Cameroon, France
Received date: 22/09/2017; Accepted date: 30/09/2017; Published date: 28/09/2017
Visit for more related articles at Research & Reviews: Research Journal of Biology
In this paper, we study electromechanical transducer, called “initial generalized electrical machine”. To describe the dynamics of electromagnetic processes, we use differential equations with periodic coefficients. In order to simplify those equations, we use Lyapunov transform to remove periodic coefficients. It is shown that the final equations of initial machine correspond to a two-phased machine with properties common for electrical machines with various applications.
Electromechanical transducer, Generalised electrical machine
The modelling of complex dynamic systems is one of the most important areas of research in the field of engineering. It is often desirable for analysis, simulation and system design point of view to represent such models by equivalent lower order state variable of transfer function models which reflect dominant characteristics of the system under consideration. A large number of methods are available in the literature for order reduction of linear continuous systems in time domain as well as in frequency domain [1-10].
The attempts to unify the piecemeal treatment of rotating electrical machines has led to generalised theory of electrical machines or two-axis theory of electrical machines. Park developed two-axis equations of the synchronous machines by making use of appropriate transformations [1,2]. Park’s ideas were then developed by Kron to deal with all rotating electrical machines in a systematic manner by tensor analysis [3]. However, Gibbs et al. simplified the work of Kron by applying matrices to the electrical machines analysis. This unified treatment of rotating electrical machines, developed by Kron is now called generalised theory of electrical machines [4]. This theory can be appreciated from the fact that a three-phase machine requires three voltage equations whereas its generalised model requires only two-voltage equations which can be solved more easily as compared to three voltage equations. Further, the circuit equations for a three-phase machine are more complicated because of the magnetic coupling amongst the three-phase windings, but this is not the case in the generalised model, in which m.m.f. acting along one axis has no mutual coupling with the m.m.f. acting along the other axis[5]. The general equations, applicable to almost all types of rotating machines, can deal comprehensively with their steady state, dynamic and transient analysis.
We consider electrical machine whose magnetic system is non-symmetric, that is having clearly expressed poles[1]. The magnetic system is characterised by the diagonal matrix of magnetic conductivities:
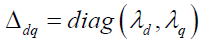
We assume that clearly expressed poles are situated in the rotor. In rotor, poles are enrolled with distributed winding F called excitation winding and non-salient n-phase winding R [3].
In notchings of cylindrical stator we have m-phase symmetric non-salient winding S[6].
An example of such a machine with the three-phase non-salient windings at stator and salient winding at rotor is shown in Figure 1.
Stator non-salient winding S is characterized by diagonal matrices of active resistances [2]
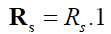 and inductances of
and inductances of 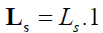
The number of turns of stator windings is defined by diagonal matrix Ws = Ws.1
Space orientation of magnetic axes of m-phase symmetric non-salient winding of stator is characterized by phase matrix [7].
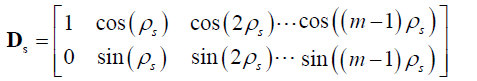
Stator phase windings are uniformly distributed along angle 2π
Magnetic axes of stator phase windings are each other deviated with same angle 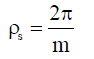
Rotor non-salient winding R is characterized by diagonal matrix of resistances 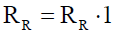 and inductances
and inductances 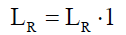
The number of turns of rotor phase windings is defined by matrix 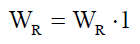
Space orientation of magnetic axes o f n-phase symmetric non-salient of rotor winding is characterized by phase matrix :
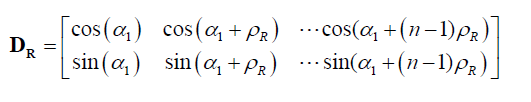
Where 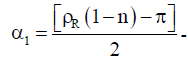 Magnetic axis deviation angle of first phase of winding relatively to magnetic symmetry d;
Magnetic axis deviation angle of first phase of winding relatively to magnetic symmetry d;
Salient excitation rotor winding F has WF turns. It is characterized by resistance RF and inductance LF The direction of winding magnetic axis corresponds with the direction of magnetic symmetry d: DF[1,0]
The main inductances of stator and rotor windings in the matrix form are:
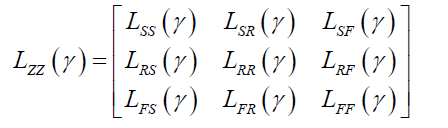
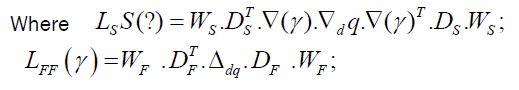
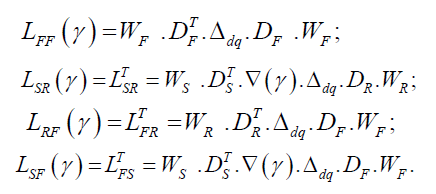
To stator and rotor windings of generalised electrical machine, we apply voltages, characterized by vectors US, UR, UF. Under actions of voltages in stator and rotor windings circulate currents IS, IR, IF.
According to the 2nd Kirchhoff’s law [8,9],
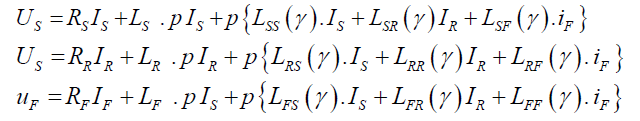
Where p - operator of differentiation
According to (1), in many cases it is convenient to represent in matrix form:
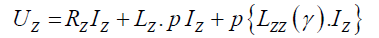 (2)
(2)
Where: 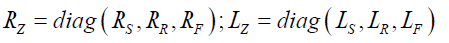
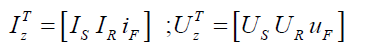
Equations (1) and (2) are called equations in real coordinate system and they include periodic coefficients.
Lyapunov Transform of Electrical Machine Equations [4,10-12]
Lyapunov transformations change the state variables and external actions thus rotation matrix becomes unit. More, initial machine windings are represented with the same number of turns, and multiphase windings are transformed to equivalent twophase windings [4].
As initial equations, we consider (1). We introduce new state variables and control signals for windings S, R, F.
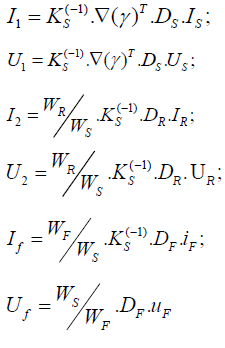
Where
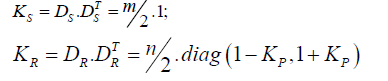
Kp – distribution coefficient of rotor winding R.
After replacement, we have:
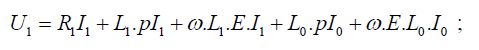
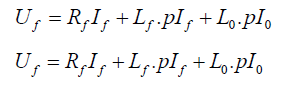
With I0 = I1 + I2 + If magnetisation current.
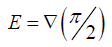 rotation matrix with angle
rotation matrix with angle 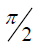
Matrices of main and mutual inductances of equivalent machine windings are considered equal:
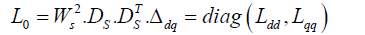
![]()
Thus, active resistances and dispersion inductances of phases of non-salient stator winding of equivalent machine are equal and correspond to those of initial generalised machine [10].
![]()
From the expressions, we have:
![]()
Finally, equations (2) correspond to two-phase non-salient rotor winding.
We have ![]()
![]()
The vectors I1, I2, If, V1, V2, are characterised by two coordinates :
![]()
In the developed form, (3) can be written as follows :
![]()
Equations (3) do not include periodic coefficients. Therefore, transformed equations from (1) are Lyapunov transformations. If we assume that angle rotation speed ω varies slower than speed of electromagnetic processes, then we can consider that equations (3) are linear [11,12].
Electrical machine with salient rotor, that has in rotor salient and non-salient n-phase windings, and also m-phase nonsalient winding in stator, possesses properties of many electrical machines used in various applications.
The dynamics of electromagnetic processes occurring in electrical machine characterise linear differential equations with periodic coefficients.
Transformed equations correspond to generalised electrical machine where:
- Stator and rotor windings have the same number of turns ;
- Non-salient m-phase stator winding is changed into two-phase winding ;
- Non-salient n-phase rotor winding is changed into two concentrated windings with direction of magnetic axes along axes of magnetic symmetry d and q.
Lyapunov transformations obtained for electrical machine by Park permit to have equations whose coefficients are constant values.
https://bluecruiseturkey.co
https://bestbluecruises.com
https://marmarisboatcharter.com
https://bodrumboatcharter.com
https://fethiyeboatcharter.com
https://gocekboatcharter.com
https://ssplusyachting.com