ISSN: 2320-2459
ISSN: 2320-2459
Carmine Cataldo*
Independent Researcher, PhD in Mechanical Engineering, Italy
Received Date: 24/08/2016; Accepted Date: 27/08/2016; Published Date: 29/08/2016
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
The purpose of this paper fundamentally lies in bringing to the attention of the reader some interesting remarks concerning the evolution of our Universe, supposed as being cyclic. Several significant hypotheses, necessary to perform a simplified modelling of the Universe evolution, as well as some noteworthy positions, elsewhere used although not properly discussed, are herein qualitatively analyzed. The existence of at least a further spatial dimension is contemplated. The Universe we are able to perceive is to be imagined as evenly spread on the surface of a four-dimensional ball. However, the so called curvature parameter is to be set equal to zero since, taking into account the extra spatial dimension, the Universe in its entirety is to be considered as being flat. Coherently with the existence of the alleged Dark Energy, we have to take into consideration a Cosmological Constant, negative in this specific case. Time is considered as being absolute. It is fundamental to underline that the variations of the cosmological distances are to be meant as exclusively metric.
Oscillating universe, Cosmological constant, Dark energy
Our universe is hypothesized as belonging to the so called oscillatory class [1]. Such a Universe, being involved in a cyclic evolution, cannot properly admit either a beginning or an end. Nonetheless, as later underlined, the beginning of a new cycle can be conventionally fixed. The existence of at least a further spatial dimension is postulated. Time is considered as being absolute.
We have to suppose that our Universe may oscillate following a simple harmonic motion. If we denote with R the radius of curvature, with Rm the amplitude of the motion (the mean radius), with H the Hubble parameter [2], and with c the speed of light, we can write, with obvious meaning of symbols and signs, the following:
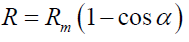 (1)
(1)
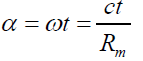 (2)
(2)
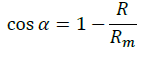 (3)
(3)
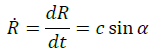 (4)
(4)
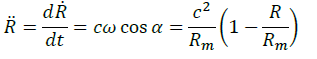 (5)
(5)
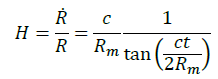 (6)
(6)
In our case, obviously, the beginning of a new cycle conventionally coincides with the point in correspondence of which the radius of curvature is equal to zero.
A three-dimensional representation (Figure 1) of the hypothesized scenario would portray our Universe as a circumference that evolves on the surface of a horn torus, following the so called poloidal direction. Each point of the circumference moves tangentially with a constant speed equal to that of light. The variations of the cosmological distances are to be meant as exclusively metric: in other terms, referring to the current observations, the expansion of the Universe should not be interpreted as a real phenomenon. More precisely, the amount of space between whatever couple of points remains the same with the passing of time. Ultimately, the Universe is imagined as being actually at rest (the real value of the curvature radius could be conventionally set equal to that of the mean one). The metric variations could be interpreted as related to the language used by the Universe to transfer information. Light is information. Light travels with a speed whose value, approximately 3.00×108 meters per second in vacuum, is constant and independent of the motion of the source. The language used to transfer information is in continuous evolution: more precisely, the speed at which the language evolves is exactly equal to the one with which light, and consequently information, propagate in vacuum.
Actually, the circumference portrayed in Figure 1 is to be considered as representative of a four-dimensional ball, whose surface, a three-dimensional curved space, can be identified with the Universe we are able to perceive. More precisely, the Universe we perceive is to be imagined as evenly spread on the surface of the above mentioned four-dimensional ball [3].
Let's consider a 4 - ball, centered at the origin, whose radius is equal to R. We know that the corresponding boundary is a three dimensional surface (a hyper sphere) characterized by the following identity
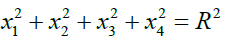 (7)
(7)
The analysis may be carried out [4] by considering the intersections between the 4 - ball, whose boundary is defined by relation (7), and the hyper planes defined by the identity
 (8)
(8)
The underlying Figure 2 obviously refers to one among the three possible three-dimensional scenarios that arise from (8).
The circumference centered at O' is simultaneously border of a disk (flat space), whose center obviously coincides with O' itself, and of a spherical cap (curved space), whose amplitude is double the angular distance between O, taken as origin, and a generic point P belonging to the above mentioned circumference. In such a Universe, and therefore net of the further spatial dimension, we perceive an arc of circumference as being a straight line segment, a spherical cap as a disk, and a hyper spherical cap as a ball.
On the other hand, taking into account the further spatial dimension, each entity perceived as merely punctual is actually the intersection between a straight line segment crossing the center of the ball and the border of the ball itself. By virtue of the hypothesized spherical symmetry, each entity we consider as punctual may be imagined as linked to its antipode. Enhancing this, we could state that each point and its antipode are actually the same thing, since they belong to the same straight line segment. As a consequence, net of the symmetry, we should rather state that what is perceived as a straight line segment is actually a circular sector, what is perceived as a disk is actually a spherical sector, and what is perceived as a three-dimensional ball is actually a hyper spherical sector. In other terms, it may be necessary to re-evaluate the very concept of mass, by taking into account the alleged existence of a further spatial dimension, so considering some sort of four-dimensional mass. Therefore, what we define as mass should be more properly considered as a linear mass density.
Obviously, coherently with the multiverse theory, the scenario just hypothesized is compatible with the existence of further universes, which in number could be both finite and infinite. In particular, referring once again to Figure 1, we could consider a further symmetry in respects to the center of the section of the torus, so as to associate each point to some sort of twin, belonging to another universe. If the first point belongs to an expanding Universe, the second belongs to a contracting Universe, and vice versa.
It is important to notice that the line of reasoning we have been following requires we formally accept the existence of the alleged Dark Energy, represented by the cosmological constant (commonly denoted with λ), negative in our case, introduced by Einstein. Moreover, although the Universe we perceive is supposed to be curved, the so called curvature parameter is to be set equal to zero. In fact, taking into account the extra spatial dimension, the Universe in its entirety is to be considered as being flat.
Considering the evolution of the Universe as an isentropic process, denoting with ρ the density and with p the pressure, the so called Friedmann–Lemaître equations [5]
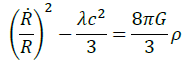 (9)
(9)
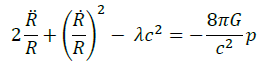 (10)
(10)
can be easily obtained once carried out the two following fundamental positions [6]
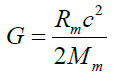 (11)
(11)
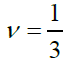 (12)
(12)
Position (11) concerns the relation between the gravitational constant and the real amount, identified with the mean value (denoted with Mm), of the mass that characterizes the Universe in its entirety (actually half the value of the mass-energy). Although slightly out of topic, it is interesting to briefly underline that, if we apply the above mentioned position to an opportune rewriting of the conservation of energy principle (the mass-energy equivalence [7]), a modified Newtonian form for the gravitational potential can be easily obtained [8]. The modified form assigns a new meaning to the coordinate that appears in the denominator of the well-known Newtonian relation. This coordinate, usually identified with the distance between the gravitational source and the point of the field in correspondence of which we want to estimate the potential, would be related both to the deformation of the spatial lattice induced by the mass and to the angular distance between the above mentioned point and the source itself. The minimum value we can assign to the coordinate in the denominator is equal to the Schwarzschild radius [9]: when this happens, we are placed in correspondence of the singularity. If we introduce the notion of relativistic gravitational potential, a fully Newtonian expression can be obtained.
Position (12) assigns an opportune value to the so called heat capacity ratio, a parameter that appears in the equation of state suggested by Zeldovich [10]
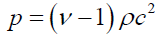 (13)
(13)
Finalized to establish a relation between pressure and density, having obviously supposed we are dealing with an ideal fluid.
It is interesting to notice that we could use the well-known relation that expresses the degrees of freedom, denoted with Df, as a function of the heat capacity ratio
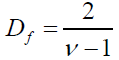 (14)
(14)
In this case we would obtain a Universe at rest, characterized by three negative degrees of freedom. In other terms, it is as if we should contemplate the existence of a further constraint, related to the extra dimension that we cannot perceive, characterized by a multiplicity equal to three. Taking into consideration the scenarios arisen from (8), we may synthesize the situation by means of the following Figure 3.
The aim of this paper simply consists in the proposal of useful remarks concerning a theory, elsewhere thoroughly expounded and herein qualitatively summarized, based upon the Cyclic Universe concept. In the light of this approach that, as suggested by the title, we have evidently chosen to follow, the discussion has been carried out by using a language that, net of some equations, should allow the reader to easily understand the core of the theory plus other fundamental implications. The hypothesized scenario is fundamentally compatible with current experimental observations. It is interesting to underline how, coherently with the so called multiverse theory, the proposed model admits the existence of further universes, besides the one we live in.