Gas-Dust Protoplanetary Disc: Modeling Primordial Dusty Clusters Evolution

Abstract

Evolution of dusty clusters in the protoplanetary gas-dust disc based on the computer modeling is addressed. The classic Newton model and method of permeable particles jointly with the developed algorithms of particles interaction are used to simulate the primordial fractal dusty clusters set up and their dependence on the parameters involved. The focus is placed on the evolution of internal structure of such clusters owing to collisions of composing original particles. The results of modeling are thoroughly discussed and are regarded as an important milestone towards the study of follow up collisional interactions of fractal dusty clusters resulting eventually to primary solid bodies formation.

Keywords

Gas-dust, Clusters, Algorithm, Collisions, Protoplanetary, Verlet.

Introduction

Study of the evolutionary processes in the early solar system and protoplanetary systems around other stars is of fundamental importance in the modern astrophysics. These processes which are originated in a primordial nebula being a fragment of a huge molecular cloud are assumed to include gas-dust disc formation around proto star followed by its radial contraction, compaction, and eventually gravitational instability. Original dust clusters of presumably fractal structure set up are assumed to be accompanied by mutual clusters/particles collisions with different relative velocities in the wide range of spatial-temporal scale.

Basically, mechanism of collisional interactions of primordial dusty structures is regarded to be responsible for the subsequent growing the embryos of primary solid bodies and eventually planetesimals. In other words, interactions through collision is addressed as the most conceivable process for dust particles to grow from an original nanometers to centimeter-meter and then even to hundred meters-kilometer size bodies for which gravity begin to affect the processes. However, the beginning phase of the growing through direct particle-particle integration seems poorly supported. Instead, the problem could be solved invoking original fluffy dust clusters of fractal nature assembled in fluffy dust aggregates which under influence of self-gravitation in the conglomerate and ambient gas pressure would coagulate evolving ultimately to primordial seeds of planetesimals. In this regard, particles growing with the involvement of primary fluffy clusters (as well as particles assembly in turbulent eddies) could be addressed as an efficient mechanism of the disc’ matter evolution.

Origin and composition of dust component in the molecular clouds, as well as the basic physical and chemical processes responsible for their evolution were studied in many publications [1-3]. One of the first attempts to study fractal dust clusters in the gas-dust nebula in terms of optical properties of graphite aggregates was undertaken in Wright [4,5], while stability of dust agglomerates depending on the mode of interactions of dust particles was investigated [6]. Model of aggregate grains formation dependent upon the charge acquired by dust grains at the process of coagulation, charge and size evolution of fractal aggregates at the collisions, as well as charge and dipole moment distribution in the dust plasma environment was evaluated [7,8]. In particular it was found that in the course of evolution dust aggregates were grown with the formation of elongated fluffy structures. Numerical modeling of the processes of compression and/or destruction of dusty aggregates upon collisions in 2D and 3D approximation was m ade by Wada et al., [9,10] who also modeled collision patterns of dust aggregates ensuring their growing [11,12]. Study of cluster-cluster aggregation revealed that original paricles shape and in particular, a deviation of monomers shape from the spherical one, significantly influences on the compactness of the resulting clusters [8].

Obviously, collisional evolution of fractal clusters is regarded as running of the compatative processes of compression and destruction. Investigation of the mechanism in the framework of mechanics of granular medium showed that both relative velocities and parameters of collisions significantly impacted on characteristics of the formed agglomerates and other complex outcomes from sticking to destruction of the clusters [13]. It is of interest the modeling of mechanisms of fluffy dust aggregates compression in the wide range of mass and physical conditions [14]. Development of primary fluffy dusty clusters of fractal internal structure and their follow up evolution were thoroughly discussed in Kolesnichenko and Marov [15,16] and various coagulation processes were addressed [17].

The above models are intrinsicaly related with general processes of the solar system formation and evolution which were discussed in the numerous papers and monographs [18-21]. Plausible scenarios are rooted in mathematical modeling of the relevant processes with involvement of some assumptions and/or constraints placed by astronomical observations of circumstellar discs and in situ study of pristine matter of meteorites. Authors’ approach to investigation of the processes involved is based on the Newton model and method of permeable particles applicable to computer modeling of both porous dusty structures and solid bodies [20,22].

Basics of the Model

Our approach to the study of clusters’ internal structure and evolution is based on the classic Newton shock model and method of permeable particles [23]. Permeable particles are regarded as model particles having an internal structure and allowing us to simplify process of collision in a dusty medium. The essence of the method is rooted in the description of particles collision through energy dissipation approach in terms of a reconstruction coefficient k depending mostly on the distance between centers of mutually penetrable particles, collisional velocity, and physical properties of particles involved. The Newton model of collisions was further advanced in terms of this coefficient. The method gave us an opportunity to take into account both internal structure of particles and complicated patterns of their interactions. .

The Newton model postulates that collision of two spherical particles having masses m_a and m_b and velocities v_a0v_b0 results in the following velocities change:

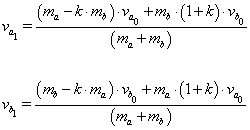
In contrast to the classic Newton model, the relations (1) contain the above mentioned reconstruction coefficient k. Approximate relations for this coefficient were designed in order to account for sufficiently well how various physical-mechanical properties effect the contact zone. Based on the method of permeable particles, the following relations for the k coefficient depending on the distance, velocity, density, and fractal dimensions of the colliding particles were suggested:

- For particles of continuous medium:

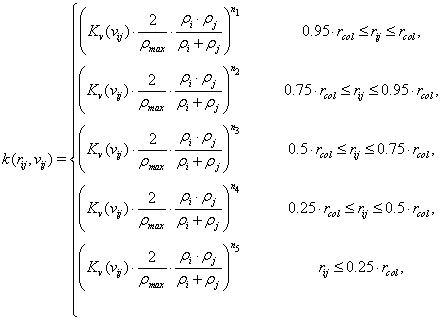
where ρ_i , ρ_j are the densities of colliding paricles; ρ_max is the maximum density of the model’s matter; r_ij is the distance between centers of colliding particles; r_col is the total of radii of colliding particles; v_ij is the relative velocity, and K_v is the parameter depending of the relative velocity.

- For particles of fractal medium:

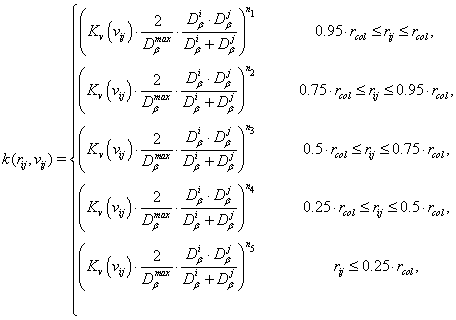
where 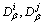, are fractal dimensions of clusters; 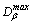is the maximum fractal dimension of the model (which is associated with the dimension of space of modeling d); r_ij is the distance between centers of clusters; r_col is the total of radii of clusters; v_ij is the relative velocity, and K_v is the parameter depending of the relative velocity.

Hereafter, for the sets of ni parameters in the relations (2, 2a) the numbers {1, 2, 3, 4, 5} were adopted. Parameter K_v describes dependence of the reconstruction coefficient k on velocity of collisions. In our model it was evaluated as

where v_ij is the velocity of particles collision and v_cr is some critical velocity v_cr depending on mechanical properties of particles.

As critical velocity v_cr entering in (3), some characteristic velocity can be adopted. For example, it could be the speed of sound in the matter of given density or the speed corresponding to the kinetic energy of colliding particles comparable with the energy required for plastic deformation or fragile destruction of a body.

Particles are assumed charged and the electric fields caused by electrostatic charges of particles were included in the collision dynamics. The following set of N equations was introduced to describe particles interaction:

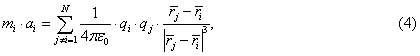
where N is the number of particles modeling colliding bodies; q_i, q_j are charges of i and j particles, respectively; а_i is acceleration of i particle; r_i, r_j are radii-vectors of i and j particles, respectively; and ε₀ is the dielectric constant.

The Model Evaluation

A few special constraints were placed when evaluating this N-body problem. They concern the algorithm of calculating forces, velocities and displacements of bodies involved. In particular, this is the necessity to derive at the every time step data on fast-going processes in the contact zone. Accordingly, the method of integration of the equations of motion should ensure the required accuracy of calculations at the short rather large time intervals. Hence choice of time interval in the numerical evaluation of the problem is regarded as the most sensitive criteria capable to provide physical consistency of the obtained results. The choice is critically dependent on minimal size of the modeled particles and collisional velocities range.

In turn, these requirements place constraints on numerical methods utilization. In particular, Runge-Kutt technique of any order turned out inappropriate since it required large amount of calculations at every time step. Verlet algorithm was more relevant and effective though less accurate [24,25]. In this approach, particle position at the next time step was calculated using its current position r_n and acceleration a_n at the previous time step, such that

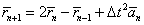
where

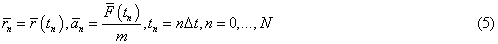
and forces F for every particle entering in (5) were calculated from the relation (4).

Let us note that in the Verlet algorithm expressions for particle velocities are not shown explicitly while they can be evaluated using routine expressions for central velocities:

Different modifications of the Verlet algorithm were suggested in order to minimize errors of calculations. One of the most efficient is the leapfrog scheme, such that the first half of particle position change is caused by its velocity at the previous step and the second half by its velocity at the current step:

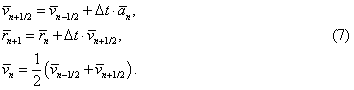
Such an approach allowed us to calculate quite efficiently both positions and velocities of particles and to keep admittable accuracy when modeling collisional processes of dust component in the protoplanetary disc. It was also possible to extend it over the study of larger solid bodies (planetesimals) evolution.

Investigation of internal structures of fractal dusty clusters requires utilization of powerful computational resources. Basically, the modern technologies of high-speed calculations using graphic accelerators of rather large capacity such as NVIDIA TESLA GPU accommodate the problem solution. This allowed us to address heterogenic processes at the juncture of physics and chemistry and in particular, to consider mechanical properties and internal structure of fractal dusty clusters jointly with physical-chemical evolution of their composed matter in the protoplanetary disc.

Results and Discussion

As it was above mentioned, of particular interest in the original evolution of gas-dust disc structure is the development of primary fluffy dust clusters, presumably of fractal internal structure. The process could be started either from a rarefied medium populated by very small particles, or a denser medium composed of dust particles. We attempted to simulate both options referred to as Models 1 and 2, respectively. The preliminary results derived from these modeling based on a few examples are discussed below. Our model may be roughly compared with those dealing with the modeling clusters collisions [10-12]. However, no results of evolution of the internal structures of original fractal fluffy dust clusters which we specially addressed in this study are available.

Model 1. In the first case, original matter entering primordial dusty clusters are assumed to form in the molecular nebula from supra-molecular complexes including dozens silicate molecules, as well as interstellar dust. Here we deal with modeling such supra-molecular complexes giving rise to the formation of spatial structures of progressively larger scale. Their follow up grow results in the formation of dusty clusters of rather complicated configurations.

Growing of fractal dusty clusters can be qualitatively represented as gluing of dust particles. In reality, properties and composition of such a cluster depends on the conditions influencing the process of growing. Numerical models involving various algorithms of particles motion and interaction in due course of clusters collision allowed us to analyze different patterns of growing structures including formation of multi-fractal configurations. Generally, they correspond to the well-known models of fractal clusters growing depending on cluster-particle(s) or cluster-cluster interactions, the mode of clusters/particles motion (either determined or stochastic) and conditions of their integration. Obviously, in the case of Brown motion diffusive particle can just glue to a cluster while clusters collision results in the formation of structure of higher fractal dimension.

Note that process of clusters’ formation and evolution in the protoplanetary disc consisting of weakly charged particles differs from that in dusty plasma [8]. Indeed, primary clusters are assumed to have characteristic size of several nm and only a few silicate molecules can fulfill such a volume. This means that particles are electrically neutral at large distances whereas inhomogeneities of the electric field caused by the spatial charges distribution in molecular objects composing dust particles should be accounted for the region of collision.

A set of the computer experiments was carried out with the following model: diameter of particles 1 nm, density 1.5·10^-21 g/nm³; charge 1 elementary (positive or negative) charge, i.e. the medium is quasi-neutral. A cubic space region of 106 nm in volume (cube size 100 nm) populated by 10000 particles was taken. In the volume of such density fluctuations of dust particles may occur due to either eddy motions of the carried flow or influence of inhomogeneous electric fields in the protoplanetary disc. The total time of one computer experiment amounted to 2·10^-5 s; continuing computation did not reveal a noticeable change in the derived structure.

As an example, Figure 1 represents visualization of numerical evaluation of the process of dust structures formation in the gas-dust cloud.

Figure 1: Evolution of dust structures in the computer modeling. Time step 1^0-12 s, the total number of time steps 2x10⁷. The finite time of the modeling 2x10^-5.

The model under consideration testified that in the processes of interaction of supra-molecular silicate complexes clusters of a linear filament structures were formed. The follow on evolution results in the formation of ring-shaped structures, as well as fluffy objects and larger particles. Some specific forms of dust structures formed in the dust component of the gas-dust cloud at the final stage of simulation are shown in Figure 2.

Figure 2: Some specific forms of dust structures formed in the computer modeling of the early gas-dust cloud evolution.

Let us note that the rate of change in structures of the forming dusty clusters decreases exponentially as free particles become exhausted and the follow up grow occurs mainly due to clusters interaction

Model 2. In the second case, numerical simulation of evolution of originally denser configurations was performed, which gave rise to the formation of larger fractal dusty clusters. Particles’ characteristics similar to those of the previous model and various numbers of such particles were taken. Additionally, for clusters composed of particles of radius r₀ and density ρ₀ the following relationships connecting density of the cluster matter and its fractal dimension could be introduced [26]:

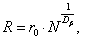
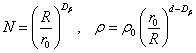
Here d is the dimension of space where the cluster under consideration is located. However, in our case a pattern of the volume fulfillment with a matter is regarded as more essential characteristic of the fractal dusty cluster. Respectively, in our calculations we used the following approximate relation to define cluster’s fractal dimension D_β:

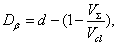
where, similar to (8), d is the dimension of space where the cluster under consideration is located, V_Σ is the total volume of particles in the cluster, and V_cl is the overall volume of the cluster. Let us emphasize that D_β serves as an important control parameter determining pattern of clusters’ behavior under collisions and simple assessment is valuable. One should admit, however, that formula (9) underestimates the real fractal dimension of a cluster and specifically, it is too sensitive to its overall volume estimation. In particular, clusters shown in Figure 3 below have fractal dimensions D_β 2.125, 2.25, 2.5 and 2.875, respectively while in the reality they are a bit higher.

Figure 3 shows an example of the results of computer modeling of dense clusters evolution comprising different number of populated particles. In every numerical experiment the final size of cluster was confined by 20 nm.

Figure 3: Fractal dusty clusters with different numbers of populated particles. Red and blue colors denote positive and negative charges.

The Models 1 and 2 are addressed as an important step towards simulation of the key mechanism of cluster simulation responsible for the follow up grow of primordial bodies in the protoplanetary gas-dust disc. Let us discuss this point in more detail.

Evidently, to study collisional evolution of fractal dusty clusters at least limited data about their internal structure are required. As the first approximation, elements of such structure (for the same numbers of particles as in Figure 3) are given in Figure 4.

Figure 4: Elements of fractal structure of dusty fractal clusters. Red and blue colors denote positive and negative charges.

We see that despite increasing number of particles in the cluster and respectively, density of its matter, a quite complicated inner organization of its spacious structure is preserved. It is worth to notice that, whereas mechanical properties of such objects can be described satisfactory in the framework of method of permeable particles we have used, additional data on dynamical behavior of the clusters colliding in the wide range of relative velocities are to be incorporated as the basis to determine a set of control parameters complementing D_β.

Basically, under collision of dusty fractal clusters change of the inner structure in the contact region and respectively, change of the cluster’s fractal dimension occur. This means that rheological properties of clusters are non-stationary. Since integrity of the cluster’s structure depends on the energy of particles coupling, there should be threshold velocity of cluster destruction at the collision. At the same time, in contrast to macroscopic objects in which mechanical destruction of particles’ coupling is in fact irreversible, in the inner structure of dusty clusters the processes of destruction and reconstruction of particles coupling are running in parallel permanently. Hence, one may assume that irreversible destruction of cluster occurs only providing the characteristic time of the couple’s reconstruction exceeds that of destruction. Some resistant exponent analogous viscosity in fluids might be introduced to characterize a threshold velocity of fractal cluster destruction at the collision as

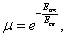
where Е_св is the generalized potential energy of particles coupling and Е_ст is the kinetic energy of collision. The ratio of the energies can be deduced from the set of numerical experiments in the wide range of the parameters involved. This is an important goal to progress with the modeling fractal dusty cluster evolution and finding constraints for original solid bodies formation in the protoplanetary disc, which is addressed as prosperity for the further study.

Conclusion

The paper develops the authors’ approach to the computer modeling dust particles and the structure of dusty clusters collisional evolution based on the modified Newton shock model and method of permeable particles, which are applicable to both fluffy dusty clusters and solid bodies [19,20]. The focus is placed on the evolution of internal structure of primordial dusty clusters owing to collisions of composing original particles. Utilization of the modern computer technologies such as NVIDIA TESLA GPU as the basic apparatus and NVIDIA CUDA as the medium of program realization allowed us to progress in the study of key processes of early evolution of the gas-dust protoplanetary discs and to get more insight into fundamental problems of solar and extrasolar systems formation.

Scenarios of particular interest in the evolution of gas-dust disc structure are the development of the primary fluffy dusty clusters, presumably of fractal internal structure. In this study, the main focus was placed on the evolution of internal structure of originally formed dusty clusters owing to collisions of composing particles. The two main models were evaluated pertinent to the processes seemingly occurring in the primordial nebula: evolution of a rarefied medium populated by very small (nanometers size) particles or evolution of a denser medium composed of larger dust particles. The preliminary results derived from these modeling allowed us to reveal the dependence of clusters’ structure and/or fractal dimension on the original parameters involved. These results are regarded as an important milestone towards in-depth study of the follow up collisional interactions of fractal dusty clusters responsible for the formation of primary embryos of solid bodies in the protoplanetary gas-dust disc around young stars including solar system origin and early evolution.

Acknowledgements

This study was supported by the Russian Fund for Basic Research (Grant # 14-02-00319) and the Program of Fundamental Study #9 of the Russian Academy of Sciences. Authors acknowledge an anonymous reviewer for the valuable comments.

References

1. TielensAGGM. Chemical and physical properties of interstellar dust. The Spectral Energy Distribution of Galaxies Proceedings IAU Symposium. 2011; 284: 72-81.
2. TielensAGGMand AllamandolaLJ. Evolution of interstellar dust. Phisical Processes in Interstellar Clouds. Reidel Publ. Co.1987; 333-376.
3. TielensAGGM,et al. Origin and Evolution of Dust in Circumstellar and Interstellar Environments. Chondrites and the Protoplanetary Disk ASP Conference Series. 2005; 341:605-631.
4. Wright EL. Long-wavelenghts absorption by fractal dust grains. The Astrophysical Journal. 1987; 320: 818-824.
5. Wright EL. Fractal dust grains around R Coronae Borealis stars. The Astrophysical Journal. 1989; 346: L89-L91.
6. Dominik C andTielensAGGM.Resistance to rolling in the adhesive contact of two elastic spheres. Philosphical Magazine A. 1995; 72: 783.
7. Matthews LS and Hyde TW. Effects of the charge-dipole interaction on the coagulation offractal aggregates. IEEE Trans. Plasma Sci. 2004; 32: 586-593.
8. Perry JD et al. The influence of monomer shape on agregate morphologies. Astronomy & Astrophysics. 2012; A99: 539.
9. Wada K, et al. Numerical Simulation of DustAggregate Collisions. I. Compression and Disruption of Two-Dimensional Aggregates. TheAstrophysical Journal. 2007; 661: 320-313.
10. Wada K, et al. Numerical Simulation of DustAggregate Collisions. II. Compression and Disruption of Three-Dimensional Aggregates in Head-on Collisions. The Astrophysical Journal. 2008; 677: 1296-1308.
11. Wada K, et al. Collisional growth conditionsfor dust aggregates. The Astrophysical Journal. 2009a; 702: 1490-1501
12. Wada K, et al. Growth and Disruption of Dust Aggregates by Collisions. COSMIC DUST - NEAR AND FAR. ASP Conference Series. 2009b; 414: 347-355.
13. Ringl C, et al. Collisions of porous clusters: A granular-mechanics study of compaction and fragmentation. The Astrophysical Journal. 2012; 752: 151-164
14. Kataoka A, et al. Fluffy dust forms icy planetesimals by static compression. Astronomy & Astrophysics. 2013.
15. Kolesnichenko AV, et al. On the Modeling Process of Aggregation of the Dust Fractal Clusters Solar System Research. 2012; 47: 6-32.
16. Kolesnichenko AV, et al. Modification of the Jeans Instability Criterion for Fractal Structure Astrophysical Objects in the Framework of Nonextensive Statistics Solar System Research. 2014; 48: 354-365.
17. Kolesnichenko AV, et al. Turbulence and Self-Organization. Modeling Astrophysical Objects. SPRINGER. ASSL, New York-Heidelberg-Dordrecht-London. 2013.
18. Johansen A, et al. The Multifaceted Planetesimals Formation Process. 2014.
19. Marov MY. The Fundamentals of Modern Astrophysics. A Survey of Cosmos from the Home Planet to Space Frontiers, SPRINGER, New York-Heidelberg-Dordrecht-London. 2015.
20. Marov MYand Rusol AV. Model of collisional interaction of bodies in the gas-dust protoplanetary disc. Dokladi RAS. 2011; 441: 464-467.
21. Marov MY, et al. From the Protostar Cloud to the Planetary System: A model for the Evolution of the Gas-Dust Disk Problem Biosphere: Origin and Evolution. (Ed. E.M. Galimov), Nova Science Publishers, NY. 2013;1: 319-404.
22. Marov MYand Rusol AV.Gas-Dust Protoplanetary Disc: Modeling Collisional Interaction of Primordial Bodies Journal of Modern Physics. 2015; 6.
23. Panovko YG. Fundamentals of Applied Theory for Vibration and Impact. Mashinostroenie PH, Leningrad. 1976.
24. Koonin SE. Computational Physics: FORTRAN Version AddisonnWesley, Redwood City, Ca.1990.
25. Rit M.Nanodesign in Science and Technology.WSP, New Jersey.2003.
26. Smirnov BM. Physics of Fractal Clusters М.Nauka. 1991.