Incompleteness of Quantum Theory on Einstein’s Program

Abstract

Adiabatic variations of frequencies lead to electromagnetic interaction constituted by progressive waves. By comparison, the consistent quantum theory, based upon time-like equations, of Dirac for fermions and of Klein- Gordon for bosons, is incomplete since it does not take account of a spacelike function u0(k0r0) to describe massive particle extension. It leads to Dirac’s distribution δ(r0) in the geometrical optics approximation, in order to handle a particle as a singularity within a continuous field, and to energymomentum conservation laws, and to least action law, with determination of the Lagrangian.

Keywords

Einstein’s program, Quantum field theory, Adiabatic invariant, Hidden variables, Wave-particle duality

Introduction

The Standard Model of particles, experimentally validated by the Higgs boson detection, represents the crowning of quantum theory. It is admitted that the whole universe is composed of fundamental particles, at one and the same time for matter and for three out of the four different interactions. They all manifest experimentally either as waves or as particles, justifying that they leans upon a quantum mechanical probabilistic framework. Since it has not still incorporated gravitation, the Standard Model describes only an incomplete aspect of the universe.

While Einstein’s contribution for relativity is admitted as essential, it appears as less important for quantum mechanics, even though his Nobel Prize was awarded for his discovery of the first quantum particle in photoelectric effect. More especially as his resolute opposition to the probabilistic framework is well known. For him, the probabilistic experimental behavior of quantum particles, like electrons, proves that the quantum mechanics description is incomplete. The statistical character of the present theory would then have to be a necessary consequence of the incompleteness of the description of the systems in quantum mechanics.

Until now, gravitation has resisted to its theoretical quantification. It remains well described by general relativity, based upon a continuous field in a classical framework, [1-5] widely confirmed by numerous experiments, by its theoretical consequences and practical applications. The graviton, as quantum particle mediating gravitation interaction, has not yet been experimentally detected and validated [6,7]. On another hand, quantum field theories of gravity generally break down theoretically before reaching the Planck scale, which determines the limit between the wave and particle behavior of quantum particles [8]. We may conclude that the discrepancy between quantum mechanics and general relativity leans on the wave particle duality, together with the classical deterministic or quantum probabilistic approaches.

In order to circumvent these difficulties, the program proposed by Einstein offered an alternating approach founded upon a general energy field.

We have two realities: matter and field. …We cannot build physics on the basis of the matter concept alone. But the division into matter and field is, after the recognition of the equivalence of mass and energy, something artificial and not clearly defined. Could we not reject the concept of matter and build a pure field physics? We could regard matter as the regions in space where the field is extremely strong. In this way a new philosophical background could be created… Only field-energy would be left, and the particle would be merely an area of special density of field-energy. In that case one could hope to deduce the concept of the mass-point together with the equations of the motion of the particles from the field e quations - the disturbing dualism would have been removed… One would be compelled to demand that the particles themselves would everywhere be describable as singularity free solutions of the completed field-equations… One could believe that it would be possible to find a new and secure foundation for all physics upon the path which had been so successfully begun by Faraday and Maxwell.

From an experimental point of view, the Einstein’s Program has been validated by the International Legal Metrology Organization when it admitted, in one hand, that the light velocity in vacuum was a primary, fundamental constant in physics, with its numerical value strictly fixed, and in other hand, when it choose one particular period an electromagnetic wave frequency as standard for measures of time.

As shown in different articles, the Einstein’s Program yields a consistent system for universe description, beside the Standard Model [8-10]. It enlarges our approach, comparably to using both eyes for tridimensional vision, or both ears for stereophonic audition. It is founded upon a scalar field propagating at speed of light c. Matter properties derive from standing waves, while electromagnetic interaction derives from adiabatic variations of frequencies. In the geometrical optics approximation, when very high frequencies are experimentally undetectable, the oscillations are hidden. This holds at one and the same time in classical relativistic and quantum frameworks, yielding their descriptions being incomplete.

In this article we propose to show how the Einstein’s program offers a means to remedy this problem, It leads to a space-like Helmoltz equation available to describe particle extension, especially in quantum theory, since the Standard Model is basically founded upon particles, in which the behaviour of massive particles is described only by time-like fundamental equations: of Dirac for fermions and of Klein-Gordon for bosons, or by their Lagrangians in variational equations. Then, particles can be indifferently extended or point-like. In accordance with experiment, they are admitted as point-like. This is necessarily a physical approximation, since their mass-energy density cannot be infinite. The Dirac’s distribution δ(r0), which offers a means to circumvent this difficulty in order to handle a particle as a singularity within a continuous field, derives itself from a space-like Helmoltz equation.

The Einstein’s Program

We restrict to summarize some equations deduced from Einstein’s program, in order to show how they are related to main equations of quantum mechanics, otherwise widely documented [11].

Kinematical Properties of Standing Fields

From the d'Alembertian’s equation describing a scalar field ε propagating at light velocity c

Derive two kinds of elementary harmonic solutions with constant frequency ω₀, with different kinematical properties. The progressive waves, retarded cos(₀t₀-k₀x₀) or advanced cos(ω₀t₀+k₀x₀), are in motion with light velocity c=ω₀/k₀. The standing waves ε₀(x₀,t₀)=u₀(k₀x₀)ψ₀(ω₀t₀)=cos(ω₀t₀)cos(k₀x₀), where space and time variables are separated, oscillate locally. They allow to define a system of coordinates at rest (x₀,t₀).

They may be considered as resulting from superposition of progressive waves.

cos(ω₀t₀+ k₀x₀)+ cos(ω₀t₀ - k₀x₀)=2cos(ω₀t₀)cos(k₀x₀) (2)

When, in a system of reference (x,t), the frequencies of opposite progressive waves are different.

cos(ω₁t-k₁x)+ cos(ω₂t + k₂x)=2 cos(ωt-βkx)cos(kx-βωt)

Where ω=(ω₁₊ω₂)/2=kc, and β=(ω₁-ω₂/ω₁+ω₂). By identification with eqn. (2), they form a standing wave in motion with a speed v=βc=(ω₁-ω₂/ω₁+ω₂)c with frequency ω=(ω₁+ω₂)/2=kc, and ω₀=√ω₁ω₂at rest, defining the Lorentz transformation between the systems of reference(x₀,t₀) and (x,t), and leading to its whole consequences.

It can be shown that the Lorentz transformation, fundamental in special relativity, is specific of c-field standing waves, particularly through the coefficient √(1-β²), which becomes (1 ± β) for progressive waves. The four-dimensional Minkowski’s formalism expresses invariance properties of standing waves at rest, in which the variables of space and time are separated, when they move uniformly with a speed v=βc<c since β is a relative difference [12]. Confirmation is found into invariant quantities obtained from four-quantities, such as coordinates 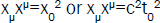, and functions 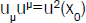or 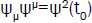. Their space-like or time-like characters are absolute, depending of their refering quantities defined in the rest system.

Since the functions u₀(k₀x₀) and ψ₀(ω₀t₀) are independent, the frequency ω₀ is necessarily constant in:

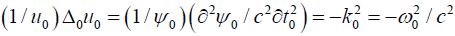(4)

The function of space u₀(k₀x₀), obeying the Helmholtz’s equation at rest Δ₀u₀+k₀2u₀=0, which becomes Δu-(1/c2) (∂2u/∂t2)+k02u=0 in motion. It describes geometric properties of standing waves. It verifies Bessel spherical functions solutions, and particularly its simplest elementary solution, with spherical symmetry, finite at of the references system,

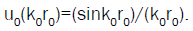(5)

Dirac’s distribution 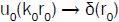is favored when frequency is tending towards infinity In Cartesian system of reference, the central extremum of an extended standing wave determines its standing position x₀=r₀=0.

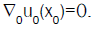(6)

In order to point out the constant frequency of a standing field, we express it as:

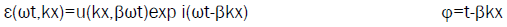(7)

The equations of special and general relativity are based on mass-points, as singularities, moving on trajectories, deriving then directly from geometrical optics approximation. Then, the kinematic properties of standing waves for a scalar field propagating at light velocity c, with constant frequency ω and velocity v, reduce formally to kinematical properties of isolated point-like matter.

Dynamical Properties of Standing Fields

In order to limit the field ε(ωt,kx) with respect to space and time, which cannot be infinite, one imposes usually boundary conditions exerted by matter [13]. It fixes the wavelength λ through k=2π/λ fixing the frequency ω or as a detector annealing it which is not felicitous from relativistic consistency since space and time operate separately

It behaves either as a source:

Two progressive waves with different frequencies ω1,ω2 propagating in the same direction at light velocity, give rise to a wave packet propagating in the same direction at light velocity. Its main wave with frequency ω=(ω1+ω2)/2, is modulated by a wave with frequency βω=(ω1-ω2)/2=Δω/2=Δkc/2, wavelength Λ=2π/βk, and period T=Λ/c. Since β<1, the modulation wave acts as an envelope with space and time extensions Δx=Λ/2, Δt=T/2, yielding well known Fourier relations Δx.Δk=2π and Δt.Δω=2π.

The boundary conditions for the scalar field ε are represented by the Fourier relations which should supplement d'Alembertian’s eqn. (1) to emphasize that field cannot extend to infinity with respect to space and time. When the difference of frequencies βω=(ω1-ω2)/2=Δω/2<< ω is very small, it can be considered as a perturbation with respect to the main frequency, βω=δω.

Monochromatic wave by a frequency Ω(x,t) can be characterized around a constant ω.

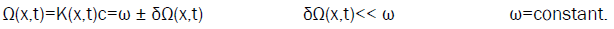(8)

This is also the definition of an adiabatic variation for the frequency. Consequently, all following properties of almost fields arise inside such a process [14]. The necessarily constant frequency of a standing wave must be considered, not as a given data, but rather as the mean value, all over the field, of different varying frequencies Ω(x,t). The perturbation frequencies δΩ(x,t) of modulation waves propagating at light velocity, behave as interactions between main waves, which yield the mean frequency ω to remains practically constant all over the space-time.

Such a behavior authorizes mathematically to derive almost fields properties from monochromatic ones, through the variation of constants method (Duhamel principle). Instead of eqn. (8), we express it, as:

(9)

Where products of second order δΩdt≈0 and δK.dx≈0, defined modulo 2π, are neglected at first order of approximation. This is equivalent to incorporate directly the boundary conditions defined by Fourier relations, in almost monochromatic solutions,

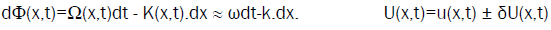(10)

Following eqn. (1), the field ε(x,t) defined by eqn. (9) verifies,

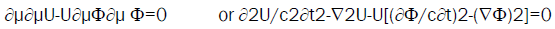(11)

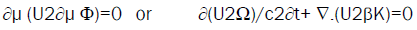(12)

These relations apply to progressive waves for β=±1, to standing waves at rest for β=0 and in motion for β<1, to monochromatic waves for ω and k constant, to almost monochromatic waves for varying Ω(x,t) et K(x,t). They lead to dynamical properties for energy-momentum conservation, and to least action principles, for standing fields and almost standing fields.

For a standing wave with constant frequencyω, either at rest or in motion, (12) reduces to:

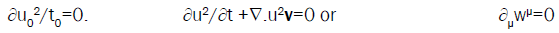(13)

Where w^μ=(u²,u²v/c)=u₀(x₀)²(1,v/c)/(1-β²) is a four-dimensional vector. This continuity equation for u² is formally identical with Newton’s equation continuity for matter-momentum density:

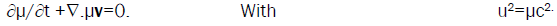(14)

By transposition, we can then admit that u2 represents the energy density of the standing field.

Centre of amplitude is taken into consideration to determine the kinematical behavior of a standing field, with position x0 defined by eqn. (6)

The position x₀ of the energy density is such that,

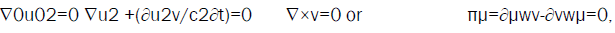(15)

The standing wave energy density u2 is spread in space [15]. It corresponds then to a potential energy density. F=-∇u2=-∇wP=is a density force, and ∂u2v/c2∂t a density momentum, and πν is a four-dimensional force density.

In eqn. (15), the vanishing four-dimensional force density tensor πμν of a standing wave, asserts its space stability remains in motion, and that the energy-momentum density four-vector wμ is four-parallel, or directed along the motion velocity v.

Eqn. (15) is mathematically equivalent to the least action relation, in which energy density wμ is a four-dimension gradient ∂μa,

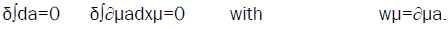(16)

When we transpose the mass density μ=u2/c2, and we take into account the identities ∇P2=2(P.∇)P+2P × (∇ × P) and dP/dt=∂P/∂t+(v.∇)P for c and v constant, after integration with respect to space, we get the equation for matter:

(17)

We retrieve the relativistic Lagrangian of mechanics for free matter Lm=-m0c2√(1-β2).

Electromagnetic Interaction

The continuity equation of an almost standing wave, expresses the total energy density, W=U²Ω=w+δW, sum of the mean standing wave w and of the interactions δW. Relation eqn. (15) becomes:

(18)

The total density force Πμν for an almost standing wave vanishes. This asserts its stability when it is in motion; Its total energy-momentum density four-vector Wμ is directed along the motion velocity v.

However it behaves as a system composed of two sub-systems, the mean standing field with high frequency Ω(x,t) ≈ ω, and the interaction field with lower frequency δΩ(x,t), each one exerting an equal and opposite non vanishing density force πμν=-δΠμν against the other [16].

By difference with the null four-dimensional density force πμν for a standing wave, only the total density force Πμν for an almost standing wave vanishes. In the first case, this asserts the space stability of an isolated moving standing wave, while in the second case, the space stability concerns the whole almost standing wave. It behaves as a system composed of two sub-systems, the mean standing field with high frequency Ω(x,t) ≈ ω, and the interaction field with lower frequency δΩ(x,t), each one exerting an equal and opposite non vanishing density force πμν=-δΠμν against the other. The mean energy-momentum density tensor πμν, no longer vanishes in eqn. (18), as previously in eqn. (15). This comes from the mean energy-momentum density four-vector wμ, which is no longer parallel, because of the opposite density force δμν exerted by the interaction.

It appears that an almost standing field behaves as a whole system in motion which can be split in two sub-systems, the mean standing field and the interaction field. Both are moving with velocity v, while exerting each other opposite forces in different directions, including perpendicularly to the velocity v. The perturbation field, arising from local frequency variations δΩ(x,t), introduces orthogonal components in interaction density force and momentum.

After generalizing relations eqn. (17) by constants variation method for mass M(x,t)=m ± δM(x,t), we get,

(19)

The density force δΠμν≠0 exerted by the interaction is formally identical with the electromagnetic tensor Fμν=∂μAν- ∂A≠0. We can set them in correspondence δΠμν=eFμ, through a constant invariant charge e, with δM(x,t)=eV(x,t)/c2 and δP(x,t)=eA(x,t)/c. The double sign for mass variation corresponds to the two signs for electric charges, or to emission and absorption of electromagnetic energy by matter. We retrieve the minimum coupling of classical electrodynamics, Pμ(x,t)=pμ+eAμ(x,t)/c, with M(x,t)c2=mc2+eV(x,t), and P(x,t)=p+eA(x,t)/c, where electromagnetic energy exchanged with a particle is very small compared to its own energy eA^μ(x,t)/c=δP^μ(x,t) << p^μ. Electromagnetic interaction is then directly linked to frequencies variations of the field ε.

Relation eqn. (19) yields the relativistic Newton’s equation for charged matter with the Lorentz force.

dP/dt=-∇m0c2√(1-β2) + e(E+v×H/c). (20)

Adiabatic Invariant

The relation eqn. (11) leads to first order approximation for an almost standing wave,

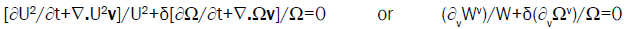(21)

with energy density W=w ± δW=μc²=μc² ± δμc², four-dimensional energy density W^ν=w^ν ± δW^ν, frequency Ω=ω ± δΩ, and four-dimensional frequency Ω^ν=(Ω,Ωv/c), leading to,

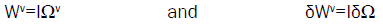(22)

When we take into account the double sign in frequency variation δΩ. The constant I is an adiabatic invariant density [17].

Integrations with respect to space of μ and I densities, lead to relations between four-energy and four-frequency through the adiabatic invariant H, formally identical with the Planck’s constant h.

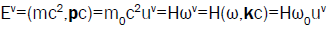(23)

For the standing wave corresponding to matter, adiabatic variations of its frequency Ω lead to electromagnetic interaction constituted by progressive waves. The energy of electromagnetic interaction derives from mass variation dE=c²dm. It leans directly upon the wave property of matter: its energy dE=hdν=c²dm derives from variations of matter energy E=hν=mc².

Applications to Quantum Theory

Relativistic Foundations

The Einstein’s program, based upon a basic scalar field propagating at speed of light, tends toward a theoretical economy by deriving mathematically, and independently of any interpretations, many different fundamental principles of Quantum Theory.

The fundamental role of the speed of light in vacuum appeared already in the beginning of Quantum Mechanics, when one noticed that, beyond its agreement with experiment, the non-relativist Schrödinger’s equation, with energy mv²/2, derived as an approximation from the relativist Klein-Gordon’s equation with energy mc². Nevertheless it remained as foundation to elaborate the theoretical and experimental Copenhagen consistent interpretation: description of a single quantum particle in motion, superposition principle, wave-particle duality behavior with uncertainty principle, Dirac’s relativist equation, the statute of the observer associated with the admitted collapse of the wave function…

Nowadays, the more general relativist Quantum Field Theory has introduced some distance with Quantum Mechanics description. For instance, a single quantum particle is no longer considered alone. It is not necessarily permanent experimentally, since it can be created or annihilated. Its experimental point-like behavior is not of prime importance, since it derives as a kind of resonance from a continuous field expressed by partial differential equations. Its mass is not a time-independent constant but varies according to the Feynman process. Its interactions verify gauge theories, with a Lagrangian invariant under continuous local transformations.

In addition to the generating time-like ψ function of quantum theory, the Einstein’s program points out the generating role of the space-like amplitude function u. It yields to define the position of a particle as a dynamical variable eqn. (6), either at rest x₀ or in x motion with x₀→x-vt, to express the continuity eqn. (15) with the energy-momentum conservation laws, and to get the least action law eqn. (16) with determining the Lagrangian eqn. (17). This is not too surprising since the amplitude function, u₀ at rest and u in motion with u₀ (x₀)→u(x-vt), remains always closely linked to the particle displacement. These properties apply both in classical and in quantum domains.

Since the Einstein’s program leans on a generating basic c-scalar field, which provides a physical general framework, it draws our attention to some main problems of Quantum Theory such as the point-like behavior of particles, and the problem of iincompleteness of quantum theory with hidden variables, which should ask to be deepened little further.

Size of Particles

It is admitted that the Standard Model represents the crowning of the Quantum theory. Consequently, the different fundamental component particles, either of matter or of interactions, are usually gathered according their spin, as bosons or fermions, which are a typical quantum property.

They are considered as point-like. From a physical point of view, it is obvious that a particle cannot be strictly point-like, since its energy density would be infinite. Since their size is not of prime importance, it does not figure usually beside their mass and electric charge. We may conclude that the description of particles by Quantum theory is not complete.

The Einstein program incites us to differentiate the fundamental particles by their relativist properties of motion, according they have a rest mass or not. The distinction is exclusive since particles without mass, like photons and gluons for interactions, move always at speed of light c: it can never be different. On the contrary, particles with mass, like fermions for matter, have a motion velocity v necessarily inferior to light speed c, following the generic relation v=βc=(ω₁-ω₂/ω₁+ω₂)c, in which the frequencies ω₁,ω₂ are hidden in the geometrical optics approximation.

As a consequence of the Einstein’s program eqn. (5), a space-like bunched function u₀(k₀r₀), with Compton’s wavelength λ₀=h/m₀c=hk₀/2π characterizes a material quantum particle. It tends towards a Dirac’s distribution u₀(k₀r₀) → δ(r₀), without the Planck’s constant, when the very high frequency becomes infinite ω₀=k₀ →∝, in geometrical optics approximation. The standing wave of the field behaves then as a free classical material particle isolated in space. Such an approach, which links the point-like aspect of particles to experimental interacting or measuring conditions, appears as more physical than the difficult and controversial collapse of the wave function ψ of Quantum Mechanics, since its time-like character is not adapted to describe any space repartition.

In quantum domain, in absence of space-like function describing the extension of a quantum particle, its point-like character is implicitly admitted because of the Planck’s constant in the Einstein’s relation E=hν for the photon, and in the de Broglie’s relation E=hν=mc² for matter.

A physical particle cannot be strictly point-like, since its energy density would be infinite. In quantum mechanics, where experimental behaviour is privileged, like in quantum mechanical Young double-slit, energy repartition is approximated by splitting it in two parts, instead of being considered as extended in space. The whole energy is concentrated in a mass-point, while the neglecting part of energy remains extended all around space-time. It behaves then as information which fixes implicitly interactions with space-time boundaries, according to eqns. (5) and (6) approximations [14-16].

For instance, such a split is clearly described by the Dirac’s distribution δ(x₀). By integration all over space, mass is totally concentrated at x₀ coordinate. As δ(x)=0 for x₀≠x₀, no mass-energy remains elsewhere. Nevertheless, since centuries, its hidden informative action had intrigued physicists about the least action principle controlling a mass-point behavior, even evoking teleological explanations: how the particle was aware of the far boundaries in order to adjust and minimize its path?

Incompleteness of Quantum Theory

Einstein considered the probabilistic experimental behaviour of quantum particles, like electrons, as a proof of the incomplete description by quantum mechanics. The statistical character of the present theory would then have to be a necessary consequence of the incompleteness of the description of the systems in quantum mechanics.

However, such incompleteness does not rest in the equations of quantum mechanics themselves. From a mathematical point of view they do not need to be modified or supplemented. They are mathematically complete inside the consistent quantum framework. For instance, in Bohm's hidden variable theory, the nonlocal quantum potential Q=-(h²∇²a)/8π²a, which constitutes an implicate hidden order in the guidance of a particle, derives from the non-relativist Schrödinger equation ih∂ψ/2π∂t=-(h²∇²ψ)/8²m, inside the solution ψ=a.expi2πS/h.

The equations deduced from Einstein’s program show particularly how, and why, quantum mechanics, and more generally quantum theory formalisms, are physically incomplete [15-17]. They do not involve the space-like amplitude function u(r₀), which describes a particle extension in its rest system, yielding many fundamental laws. It supplements the consistent quantum framework, based upon time-like equations: of Klein-Gordon for bosons, (from which derives the non-relativist Schrödinger equation), of Dirac for fermions, or of introduced Lagrangian densities for massive particles.

As well known, the distinction between time-like and space-like characters is absolute.

Conclusion

Consequently, the quantum framework of the Standard Model of particles, which is theoretically consistent and complete, remains unaffected by the Einstein’s program. However, the introduction of an extraneous space-like function for the elementary particles description emphasizes that their admitted size, with zero dimension, is physically only an approximation. This points out a problem which, according to Einstein, merits probably to be more investigated: Above all, however, the reader should be convinced that I fully recognize the very important progress which the statistical quantum theory has brought in physics.... this theory is until now the only one which unites the corpuscular and undulatory dual character of matter in a logically satisfactory fashion; and the (testable) relations, which are contained in it, are, within the natural limits fixed by the indeterminacy-relation, complete. The formal relations which are given in this theory—i,e, its entire mathematical formalism—will probably have to be maintained, in the form of logical inferences, in every useful future theory.

References

1. Cui Y, et al. Luminescent functional metal–organic frameworks. Chemical reviews. 2011;112:1126-1162.
2. Harbuzaru BV, et al. Metal–organic nanoporous structures with anisotropic photoluminescence and magnetic properties and their use as sensors. AngewandteChemie International Edition. 2008;47:1080-1083.
3. Yaghi OM, et al. Reticular synthesis and the design of new materials. Nature. 2003;423:705-714.
4. Banerjee R, et al. High-throughput synthesis of zeoliticimidazolate frameworks and application to CO2 capture. Science. 2008;319:939-943.
5. Dey C, et al. Crystalline metal-organic frameworks (MOFs): synthesis, structure and function. ActaCrystallographica Section B: Structural Science, Crystal Engineering and Materials. 2014;70:3-10.
6. Burtch NC, et al. Water stability and adsorption in metal–organic frameworks. Chemical reviews. 2014;114:10575-10612.
7. Kreno LE, et al. Metal–organic framework materials as chemical sensors. Chem. Rev. 2012;112:1105-1125.
8. Sun F, et al. Tandem postsynthetic modification of a metal–organic framework by thermal elimination and subsequent bromination: effects on absorption properties and photoluminescence. AngewandteChemie 2013;125:4636-4641.
9. Allendorf MD, et al. Luminescent metal–organic frameworks. Chemical Society Reviews. 2009;38:1330-1352.
10. Valeur, Bernard, and MárioNunoBerberan-Santos. Molecular fluorescence: principles and applications. John Wiley & Sons, 2012.
11. Shustova, Natalia B, Brian D. McCarthy, and MirceaDinca. "Turn-on fluorescence in tetraphenylethylene-based metal–organic frameworks: an alternative to aggregation-induced emission. Journal of the American Chemical Society. 133.50 (2011): 20126-20129.
12. Chen W, et al. Photoluminescent metal− organic polymer constructed from trimetallic clusters and mixed carboxylates. Inorganic chemistry. 2003;42:944-946.
13. Senchyk GA, et al. AgI/VV heterobimetallic frameworks generated from novel-type {Ag2(VO2F2)2 (triazole) 4} secondary building blocks: a new aspect in the design of SVOF hybrids. Inorganic chemistry. 2012;51:8025-8033.
14. Manna B, et al. Anion‐Responsive Tunable Bulk‐Phase Homochirality and Luminescence of a Cationic Framework. Chemistry-A European Journal. 2014;20:12399-12404.
15. Zhao B, et al. Coordination polymers containing 1D channels as selective luminescent probes. Journal of the American Chemical Society. 2004;126:15394-15395.‏
16. Liu W, et al. Lanthanide coordination polymers and their Ag+-modulated fluorescence. Journal of the American Chemical Society. 2004;126:2280-2281.‏
17. Dang S, et al. A layer-structured Eu-MOF as a highly selective fluorescent probe for Fe 3+ detection through a cation-exchange approach. Journal of Materials Chemistry. 2012;22:16920-16926.‏