ISSN: 2322-0066
ISSN: 2322-0066
Russian Federal Nuclear Center – All-Russia Research Institute of Experimental Physics, Institute of Physics of Explosion, Russia
Received Date: 27/12/2016; Accepted Date: 01/02/2017; Published Date: 08/02/2017
Visit for more related articles at Research & Reviews: Research Journal of Biology
In this work, we review the results of the development of phenomenological method for describing formation and growth of nanostructured objects with strong interatomic bonds. It is assumed that the growth of nanostructures is caused by their phonon excitations and vibrational interactions, leading to mutual compensation of free electronic bonds of “boundary” (i.e., surface) atoms in adjoining objects and to consolidation of these objects into more large patterns, which are compact clusters. The clusters reveal collective quantum properties, namely, excitations of quasi-particles – phonons. A proposed cluster mechanism of formation of macroscopic diamond particles from nanodiamonds made it possible to describe all data available at that instant, concerning man-made diamonds produced during both static and dynamic synthesis. A proposed model of formation of biological nanoobjects and mesoobjects gives formally calculated sizes, which correspond to characteristic dimensions of protein nanoparticles. In addition, the model provides a mesoscopic range of sizes, which is in keeping with characteristic dimensions of cells as well as of simplest organisms.
Mesokinetics, Formation and growth, Nanostructured objects, Strong bonds, Phonon excitations
Multiple scientific works are devoted to elaboration of methods for making nanostructured substances as well as for investigating a behavior of synthesized samples at different conditions [1-8]. The study of formation, growth and behavior of nanostructures is a constituent part of mesophysics as the science dealing with the substance, revealing classical and quantum features simultaneously in the field of spatial scale 10–9–10–7 m. Quantum features of a substance are most conspicuous with the availability of strong bonds between atoms. We consider two types of objects: 1) crystals whose lattice is formed by atoms of the same type oscillating as harmonic oscillators with typical frequencies ~1012–1014 s–1 (“atomic crystals”), and 2) crystals generated by macromolecules exhibiting both oscillating nature of internal motions with the given frequencies and rotary isomerism with the frequencies ~1010–1011 s–1 (“molecular crystals”). In order to understand how collective quantum properties of structures affect their typical sizes as the first type objects, it is reasonable to consider crystals with covalent carbon bonds C–C, i.e. diamonds characterized by pronounced phonon effects associated with exchange interaction of atoms. As the second type objects, it is reasonable to consider protein nanoparticles consisting of amino acid molecules since the latter are characterized by strong bonds of the C–C, C–N and C–O type that provide high-frequency oscillating term of internal motions, and also by rotary isomerism and low-frequency component of spin-lattice relaxation (107–1010 s–1) that develop conformational motions.
Molecular dynamics methods and quantum-statistical models [7,8] are applied to describe the evolution of nanostructures. In the present work we review the results of the development of phenomenological method [9] for describing a growth of nanostructured objects with strong interatomic bonds. It is assumed that the growth of nanostructures is caused by their phonon excitations and vibrational interactions, leading to mutual compensation of free electronic bonds of “boundary” (i.e., surface) atoms in adjoining objects and to consolidation of these objects into more large patterns. It should be noted that the proposed method in no way can replace the above fundamental methods of investigation of mesocosm dynamics. On the other hand it is well known that when interacting with environment, physical objects never discover their complete internal complexity potential. Hence incomplete or even phenomenological description of physical phenomena or physical objects sometimes responses better to the main point, and to the understanding of what is going on [10]. Since the proposed in [9] kinetic approach provides an adequate description of processes in microcosm, it is possible to try to use it for considering object growth processes in mesoscopic scales.
Our review consists from two parts. In Part 1 we describe cluster mechanism of diamond synthesis from carbon nanostructures. In Part 2 we will try to reveal cluster mechanism of formation of biological nanoparticles and mesoobjects from amino acids molecules.
Kinetic Approach
Traditionally, the phase transition from graphite to diamond at high pressures and high temperatures is treated as the main mechanism of diamond formation [3]. Accordingly to notions presented in work [11] we assume that the structure of initial carbon material under external action fails into single fragments composed of carbon atoms such as planar graphite hexagons, molecules of the benzene carbon skeleton type, cyclane, etc. The collisions of these fragments can bring about the formation of molecules with a cyclohexane carbon skeleton, which, owing to the mutual orientation of carbon atoms, in essence, are seeds of the diamond crystal structure. It should be noted that, in the scheme under consideration, we deal not with molecules of different hydrocarbons, but with their carbon skeletons, i.e., the structures with free external bonds formed, for example, upon breaking of the C–H and C–O type bonds. The collisions between the molecules with the cyclohexane carbon skeleton lead to the mutual compensation for the free bonds and appearance of small-sized clusters whose growth results in the formation of carbon mesostructures with the short-range crystal order that matches the diamond lattice. The interaction of these mesostructures with each other and seeds gives rise to a quasi-long-range order, which corresponds to the formation of nanodiamonds. The coalescence of nanodiamonds is responsible for the growth of the diamond crystals, which, in principle, can occur under metastable conditions: at “zero” pressure and increased residual temperatures. Therefore, in the proposed model, the synthesis of diamond from different solid carbon forms is associated with the formation and growth of small-sized crystalline diamond-like structures.
In accordance with notions [11] it can be believed that the phonon excitations of carbon objects are crucial in the considered processes due to the anomalously high Debye temperature of the diamond, which is equal approximately to 2000 K and is comparable to the temperatures (T ~ 103 K) reached in the diamond synthesis. It is natural to expect that, when the duration of the external action on the objects is considerably longer than the characteristic travel time of vibrational excitation in them, the probability that the excited lattices of touching clusters are joined owing to the mutual compensation for the free external bonds of the “boundary” (i.e., surface) atoms is high. In this case, the objects are linked together with the formation of covalent bonds, and the particles increase in size. Analytical model for describing such process was developed in [9].
Diamond Synthesis at Moderate Environments
At moderate conditions of synthesis, when an environment temperature is comparable with the Debye parameter, growth of mean size of particles with the time t is described by the following formulae deduced in [11]:
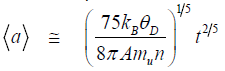 (1)
(1)
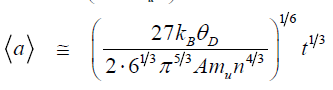 (2)
(2)
Here, is the Boltzmann constant, is the Debye parameter, A is mass number, is atomic unit of mass, n is concentration of atoms in crystal lattice. Formula (1) corresponds to a small flux of seeds (nanodiamonds), when an average size growth occurs as a result of “particle-seed” – type interaction. Formula (2) corresponds to a large flux of seeds, when growth occurs as a result of “particle-particle” – type interaction. The mean sizes of the synthesized crystals do not depend on the initial size of seeds (nanoclusters), which implies that the system “forgets” the initial conditions, and the particles grow in accord with the dynamics of the macroscopic crystal lattice.
The proposed in work [11] mechanism of macroscopic diamond particle formation from nanodiamonds covered all the available at that time data related to both artificial diamonds produced under static and dynamic synthesis, and natural diamonds that could have been formed as a result of cataclysm, e.g. impact of meteorite. Within a unified approach [11], one can attempt to consider syntheses of diamond from different solid carbon forms subjected to mechanical loads that correspond to the lower boundary of the diamond stability region [3] and prevent the formation of a liquid phase.
In experiments on the shock-wave synthesis of diamond from fullerites which was analyzed in [11], the time of the heat wave propagation from the shock-heated sample to the surrounding matrix was estimated to be equal to thp~ 10–2 s. It can be believed that the carbon sample was rapidly cooled, and the diamond phase was quenched for the time thp. The estimates performed from relationships (1) and (2) at t ~ 10–2 s show that the mean sizes of diamond particles are equal to about 4 μm and about 1 μm, respectively, which coincides in the order of magnitude with the experimental data.
The static synthesis of diamond was analyzed in [11]. From formula (1), it follows that the “faster” mechanism of the attachment of small-sized nuclei to the large-sized particle provides a way of growing the diamond crystals with characteristic sizes from 0.3 to 2 mm for the time interval from 10 min to one day. The particles with these sizes in the order of magnitude are formed during the above times in high-pressure chambers under the conditions corresponding to the lower boundary of the diamond stability region in the phase diagram of carbon. In the static synthesis of diamond from carbon nanotubes, it was found that the maximum size of crystallites formed in a high-pressure chamber for 30 s is equal to 20-50 μm. The diamond crystals of size 150–200 μm were obtained in parallel experiments with the use of graphite. The latter values are in satisfactory agreement with the estimate made by formula (1), according to which the mean size for the given time is equal to about 100 μm. At the same time, the estimate from relationship (2) leads to a mean size of about 10 μm, which agrees in the order of magnitude with the sizes of diamond prepared from nanotubes.
It was believed in [11] that the model proposed is also applicable to investigations into the growth kinetics of natural diamond crystals formed in the earth’s cataclysms, for example, a meteorite impact. The estimates obtained from formula (2) for a slower process demonstrate that diamonds of sizes 1–10 cm can grow for 8·103 – 8·106 years. These times are substantially shorter than the Earth age, which is likely of an order of 109 years. This suggests the pulsed (accidental) character of the formation and growth of natural diamond.
A good agreement between the results of calculations performed work [11] and the available experimental data confirms the adequacy of the proposed model for the growth of diamond-like structures under loads excluding the formation of liquid phase. All the foregoing corroborates the hypothesis on the decisive role of vibrational interactions between crystalline objects with the anomalously high Debye temperature in the dynamic and static syntheses of diamond from different solid carbon forms such as organic compounds, nanodiamonds, fullerite, graphite, and nanotubes.
The cluster mechanism proposed in [11] for formation of macroscopic diamond particles from nanodiamonds made it possible to describe all data available at that instant, concerning both man-made diamonds produced during static synthesis and dynamic synthesis, and natural diamonds, which can be formed as the result of the earth’s cataclysms, for example, a meteorite impact.
Diamond Synthesis at Severe Conditions
An example of using the method [9] is explanation and description of diamond synthesis in conditions of cavitation experimentally studied in [13,14]. In the experimental setup used in [13], the excitation of cavitation in benzene led to the formation of organic polymers with an admixture of nanocrystalline aggregates representing solid carbon. A certain fraction of these aggregates contained a diamond phase with the crystallite sizes of 10–30 nm. The ultrasonic cavitation in liquid suspensions of graphite particles [14] led to the development of extremely high temperatures T=1000–7000 K at the stage of bubble collapse on a nanoseconds time scale. An analysis of the obtained products revealed the presence of diamond particles with average dimensions about 10 μm and small dispersion (± 0.5 μm). It was suggested that the small dispersion was related to a rapid termination of the synthesis behind the propagating shock wave. It was pointed out in [14] that the appearance of monodisperse diamond crystals with indicated dimensions for the short periods of time characteristic of ultrasonic cavitation cannot be explained in terms of the above models of diamond cluster growth [11] and, hence, the formation of diamonds under extreme conditions should proceed according to an alternative mechanism, although no such mechanism was proposed in [14].
In work [15] a solid stage of the process is considered analytically, at this stage diamond particle growth under extreme condition occurs. Let us assume that, under the conditions of cavitation, the diamond phase can nucleate according to the above kinetic mechanism [11] for a time on the order of 10–12 s as a result of the decomposition and rearrangement of the initial carbon structure. The subsequent coalescence of these primary nuclei leads to the formation of crystalline clusters (nanodiamonds). The nanodiamonds formed during the cavitation in liquid suspensions can be modeled by a crystalline core surrounded by an amorphous shell with a thickness on the order of one atomic bond length. As a result of the phonon excitations in crystalline nuclei of nanodiamonds, the unsaturated electron bonds on the surface of these cores exhibit mutual compensation and entanglement, which lead to the growth of particles of the diamond phase.
According to the notions developed in [9,15], the formation of nanodiamonds under conditions of a small flux of nanoparticles, whereby each particle occupies a place on the cluster surface prior to the onset of interaction with the next nucleus, can be described by the following law, which describes the growth of the average cluster size with the time:
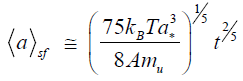 (3)
(3)
Here,is the minimum size of a diamond phase nucleus possessing a quasi-far-range crystalline order. Considering the case of translation symmetry, we can assume that this minimum size is a* = 2ac, where ac is the crystal lattice parameter. Using the approach [9,15], we obtain the following expression for the particle growth under conditions of central collision (cc) of clusters:
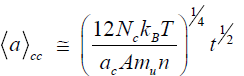 (4)
(4)
For an average temperature in the above indicated interval (T=4000 K) these formulas show that nanodiamonds with dimensions of 25–45 nm can form within a time period of t=10–9 s. These estimations approximately correspond to the experimental data reported in [13].
In order to describe the subsequent growth of the diamond phase, let us consider the regimes [15] of isotropic impact loading and shear interaction of the particles. In the case of a homogeneous impact loading of the initial sample, the phonon excitations involve all atoms of the interacting particles and the mean size of the crystalline phase increases with time according to the following formula.
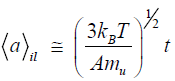 (5)
(5)
This formula shows that, at T=4000 K, diamond particles with dimensions of about 10 μm (i.e., such as were obtained in [14]) can form in an impact time of t=3.10–9 s. In the case of tangential friction (shear regime), the excitations involve the surface layers of particles with thicknesses on the order of the crystal lattice parameter ac and the growth is described by the following law:
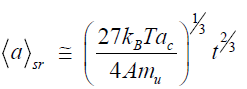 (6)
(6)
This formula shows that the size of 10 μm is reached at t=4·10–7 s.
It can also be suggested that the formation of diamond particles in the solid phase under the conditions of ultrasonic cavitation in liquid suspensions of graphite nanoparticles can proceed both at the final stage of collapse in the cavitating bubble and in the course of subsequent expansion of the products of this collapse.
Thus, the cluster model proposed previously in [11] for the formation of diamond from various solid forms of carbon has been modified in [15] so as to apply to temperatures that significantly exceed the Debye parameter. The obtained laws of diamond phase growth can be useful for the prediction and analysis of experimental results on the diamond synthesis under severe conditions.
The proposed cluster mechanism of formation of macroscopic diamond particles from nanodiamonds made it possible to describe all data available at that instant, concerning man-made diamonds produced during both static and dynamic synthesis.
https://bluecruiseturkey.co
https://bestbluecruises.com
https://marmarisboatcharter.com
https://bodrumboatcharter.com
https://fethiyeboatcharter.com
https://gocekboatcharter.com
https://ssplusyachting.com