ISSN: 2322-0066
ISSN: 2322-0066
Samuel Bonaya Buya*
Mathematics/Physics Teacher at Ngao girls, Secondary School, Kenya
Received date: 23/06/2017; Accepted date: 28/07/2017; Published date: 07/08/2017
Visit for more related articles at Research & Reviews: Research Journal of Biology
I present methods that can be used to obtain algebraic solution of polynomial equations of degree five and above. In this contribution I look into methods by which higher degree polynomial equations can be factorized to obtain lower degree solvable auxiliary equations. The factorization method has been used to successfully solve quartic equations. A careful selection of the appropriate factorized form can bear much fruit in solving higher degree polynomial. Ehrenfried Walter von Tschirnhaus (1651-1708) invented the Tschirnhaus transformation. The Swedish algebraist Erland Bring (1736-1798) showed by a Tschirnhaus transformation that the general quintic equation can be transformed to the trinomial form. The English mathematician George Jerrard (1804-1863) generalized this result to higher degree polynomial. The possibility of solvability of higher degree polynomials would pave way for transformations that can reduce higher degree polynomials to their trinomial form. The Newton Identity relates the roots of polynomials with their coefficients. It is possible to introduce an instantiation of this formula where a root of polynomial is correlated to its coefficient. This is in order to facilitate easy reduction of polynomials to lower degrees for solvability. Once a polynomial is reduced to solvable lower degree forms and there consequent roots it is possible covert it as a root of the degree of original polynomial. The paper will seek to address briefly on the things highlighted in this abstract. Solvability of higher degree polynomials will of necessity call for a re-examination of the Abel-Ruffini impossibility theorem and the Galois Theory at large.
Algebraic solution of Quintic, Sextic and septic equations; General solution of polynomial equations; Review of Galois theory; Abel-Ruffini impossibility theorem; Lagrange and Galois resolvents
Background and Literature Review
Several mathematicians have tried to obtain a radical solution of the quintic equation. Up to the past century no one succeeded to come up with its general algebraic solution. Joseph Louis Lagrange (1736-1814) wrote a book [1] in which he examined previous attempts to solve the quintic equation. Lagrange [2] introduced the concept of the Lagrange Resolvent and noted that the Resolvent worked for cubic and quartic equations but failed to achieve the desirable results for higher degree equations. In his contribution it is noted that the degree of the Resolvent of a polynomial is equal to the order of the sn. This means any attempt of solving a polynomial of degree 5 would lead to an equation of degree 120 (which is also the order of s5)
In math a Resolvent is an equation upon whose solution the solution of a problem depends.
For the purpose of this paper I will touch on a few highlights of the Lagrange Resolvent.
For an nth degree polynomial the Lagrange Resolvent is defined as
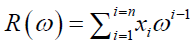 (1)
(1)
where x_i, i=1,. . . , n, are the roots of the equation and ω is an nth root of unity.
For a cubic equation it means by the method of Lagrange resolvents,
z = x1 + x2 ω + x3ω2
Where xi are the roots of the cubic equation and ω is the cube root of unity. By permuting these roots into each other we get six different values of z.
The six different permutations are:
z1 = x1 + x2ω + x3ω2
z2 =ωz1
z3 =ω2 z1
z4 = x1 + x3ω + x2 ω2
z5 =ωz4
z6 =ω2 z4
The equation 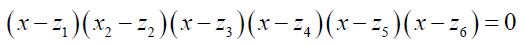 is then formed.
is then formed.
We then find out that
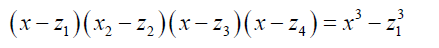
And
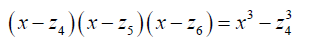
So that
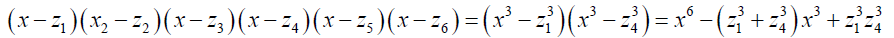
The above equation is quadratic in x3.
The importance of the Lagrange resolvent is its ability to solve the cubic and even quartic equations. However if a similar construction is made with a quartic equation it would yield a solvable equation of degree 24. With the quintic equation however the Lagrange Resolvent would yield an unsolvable degree 120 polynomial equation. The Lagrange resolvent failed to provide a way forward to the solution of higher degree polynomial equations.
In 1799 Paolo Ruffini provided an incomplete proof of the impossibility of solving quintic and higher degree equations. In 1826 Niels Henrik Abel [3] provided a proof to show the impossibility of solving general degree five equations and above. Evariste Galois (1832) [4] constructed the Galois resolvent that is, if we have a polynomial with coefficients in a field F then the resolvent:
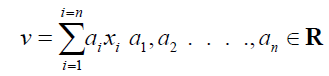 is a Galois resolvent if one gets n! different functions when permuting the roots with each
other.
is a Galois resolvent if one gets n! different functions when permuting the roots with each
other.
The Galois resolvent is then used to form the polynomial 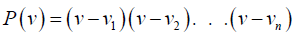 where vi are symmetric functions
of the roots of the polynomial. With His group theory Galois made the observation that because it is impossible to have a chain
of groups for permutation groups of S n ≥ 5 then it is impossible to solve algebraically equations of degree five and above. Galois
Theory identified criteria for obtaining solvable cases.
where vi are symmetric functions
of the roots of the polynomial. With His group theory Galois made the observation that because it is impossible to have a chain
of groups for permutation groups of S n ≥ 5 then it is impossible to solve algebraically equations of degree five and above. Galois
Theory identified criteria for obtaining solvable cases.
Bring [5] and Jerrard [6] how the general quintic equation can be reduced to trinomial form
There is the Dummit proof theorem [7] which states that the irreducible quantic 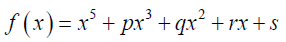 is solvable in
radicals if and only if the sextic equation
is solvable in
radicals if and only if the sextic equation
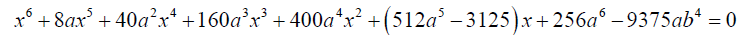 has a rational root. If this is the case the
sextic factors into the product of a linear polynomial (x - θ) and an irreducible quintic g(x). I will show later in this paper how this
sextic can be reduced to linear and quadratic factors.
has a rational root. If this is the case the
sextic factors into the product of a linear polynomial (x - θ) and an irreducible quintic g(x). I will show later in this paper how this
sextic can be reduced to linear and quadratic factors.
Edward Thabo Motlotle [8], in his 2011 master’s thesis managed to present a formula for solving the Bring-Jerrard quintic equation using the Newton’s sum formula. In his contribution Motlotle convincingly argued that Abel’s impossibility proof has been misconstrued by many as meaning that no general algebraic solution of the quintic equation is attainable. He showed that such a formula in unattainable only within a field of Rational numbers. He then moved on to deriving a formula. Motlotle demonstrated that the Galois group associated with the general quintic equation is solvable over algebraic numbers.
Motlotle identified a pattern that flows from the work of del Ferro (1465 – 1526) and Ferrari (1522 – 1565) in their approach to the cubic equation. The pattern he identified was of the form:
rn − K − L = 0
Statement of the Problem
Could it be possible that the Galois Theory is incomplete in its treatment of higher degree polynomials? What about the Lagrange and Galois resolvents, are they all that the mathematics principles can provide in the solution of higher degree algebraic equations? Is it possible to come up with factorized forms that can be used to solve higher degree polynomials? Is it possible to come up with instantiations of the Newton’s sum formula? In the most general sense, the newton’s identity is a correlation between roots and coefficients of a polynomial equation. Could it be possible to come up with a correlation connecting the coefficients of a polynomial to a single root? If such a correlation can be obtained should make it possible to factorize a degree n polynomial to linear and degree n-1 factors. Is it possible that after reducing a higher degree polynomial and obtaining solutions in terms of lower degree polynomial to covert the same in forms of roots of the original polynomial?
In this paper I will seek to present methods of factorizing higher degree polynomial s to solvable forms. I will seek to present an instantiation of Newton’s identity that can be used factor linear factors from out polynomial equations.
I will seek to show that the sextic equation of Dummit’s proof theorem is reducible to quintic and linear factors.
The main objective of this paper is to show that algebraic equations of degree five and above are solvable algebraically.
Specifically I will seek to present a method by which a degree n polynomial can be factored to a linear factor and degree n-1 polynomial.
I will seek to present solvable factorized forms of polynomial equations.
I will seek to present a method of converting back a root to nth root form where the polynomial has been reduced to lower forms and roots have obtained in lower forms.
Approach and Justification
Abstract algebra asserts the impossibility of solving a general algebraic equation of degree n ≥ 5 because the Alternating group is simple that is it does not permit normal subgroups.
In the paper “Solution of Solvable Irreducible Quintic Equations, without the aid of a Resolvent Sextic” [9], George Paxton Young asserts the irreducibility of the Bring-Jerrard quintic equation.
G.P. Young, on the basis of irreducibility of the quintic equation in the trinomial form, argues further that it cannot be solved algebraically except in particular cases.
The Bring-Jerrard quintic equation is given by:
x5 + px + q = 0 (2)
G.P. Young then brings in exogenous quantities or parameters by which the most general solvable cases of the Bring-Jerrard quintic equation can be determined algebraically.
Young introduced the rational functional relations 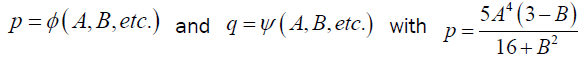 and
and 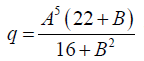 as his most general cases. Then he was able to determine the roots in terms of A, B.
as his most general cases. Then he was able to determine the roots in terms of A, B.
I will seek to use the approach of Young to propose a possible method of solving the quintic equation and higher degree equation. Since the parameterization of Young did not yield a complete solution, I will seek to modify it to achieve a general solution.
The trinomial quintic equation has two parameters. I seek to introduce a parameterization in which one of the parameters is a root of the algebraic equation and the other parameter/parameters are the coefficients of the equation. Such a parameterization is as a matter of fact an instantiation of the Newton identities. Newton identities can be viewed as a parameterization which correlates the roots and coefficients of the polynomial equation.
To reduce the Bring-Jerrard quintic, I introduce the functional relation p =φ ( A,q) Then the roots will be determined in terms of A, q.
It is desirable to express the roots in terms of p, q. In such cases a functional relationship between A, p and q must be sought for, that is:
A = f ( p, q)
Whenever such relations are found then the polynomial has a general algebraic solution.
In this research I will extend my argument to irreducible algebraic equations of degree n. I will show that such equations are reducible in the most general sense. Thus I will show that algebraic equations of higher degree are always reducible.
In this paper partial reference will also be made to my previous contributions in the area [10,11].
I will seek to show that there are factorable forms that are very effective in solving higher degree polynomials.
In the event formulae of a polynomial equation is given in terms of lower degree polynomials because of factorability, I will seek to present a method in which the root can be converted to an order equal to the degree of the polynomial.
Method
Consider the Bring- Jerrard quintic equation
x5 + px + q = 0 (3)
The functional relationship p =φ ( A,q) (4)
can be used to reduce it to quartic and linear factors.
More definitely:
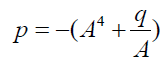 (5)
(5)
Using such a relationship as above the Bring-Jerrard quintic equation can be reduced to:
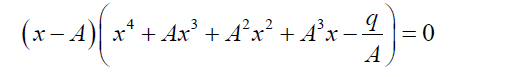 (6)
(6)
Examples
To illustrate, if in the above quintic equation, if we take A = 1 and q =1, then p = -2. One of the roots is therefore 1.
If we take A = 5 and q = 10 then p = -627. One of the roots of quintic equation is 5 and so on.
Thus the Bring-Jerrard quintic equation is solvable in the parameter A and q. It is however more desirable to solve it in parameters p and q. A further analysis shows it is still possible. This will be discussed further in the paper.
By the transformation used by Bring, the sextic equation can be brought down to the form:
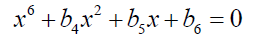 (7)
(7)
The functional relation 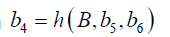 (8)
(8)
can be used to reduce sextic to linear and quintic factors.
More definitively:
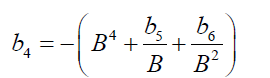 (9)
(9)
In this case the sextic equation 0.6 is reduced to:
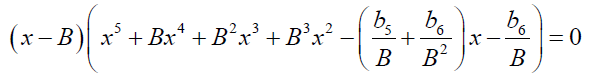 (10)
(10)
The expansion of equation 0.6 will result in equation 0.6
Thus the sextic equation 0.6 is solvable in the parameters B, b5 and b6
Examples
If in the above sextic equation we take 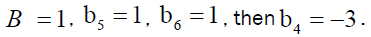 One of the roots of the sextic equation is 1.
One of the roots of the sextic equation is 1.
If we take B = 5 , b5 = 4 , b6 =1, then 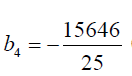 0ne of the roots of the sextic equation is 5.
0ne of the roots of the sextic equation is 5.
The polynomial equation of degree n can be brought down to the form:
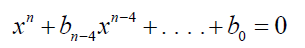 (11)
(11)
The functional relation 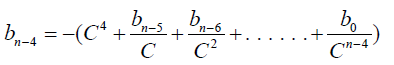 (12)
(12)
In this case the polynomial equation 0.9 can be reduced to the form:
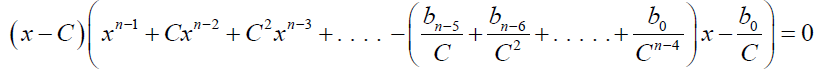 (13)
(13)
Thus the polynomial equation 0.9 is solvable in parameters 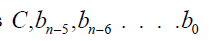
It is however more desirable to obtain solutions of higher degree polynomials in terms of the endogenous parameters.
Note the above parameterizations involve connecting between a root of a polynomial equation and its parameter.
The Newton’s sum formula can be viewed as a generalization of the above instantiation.
There is the Dummit proof theorem [7], [8] which states that the irreducible quantic 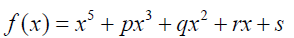 is solvable
in radicals if and only if the sextic equation
is solvable
in radicals if and only if the sextic equation 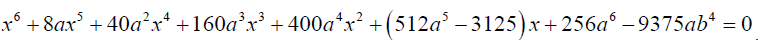 (14)
(14)
has a rational root. If this is the case the sextic factors into the product of a linear polynomial (x - θ) and an irreducible quintic g(x).
In view of the above analysis the above sextic equation can be factorized if we can take:
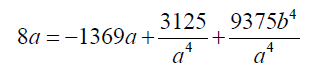 (15)
(15)
so that the 12 now takes the form:
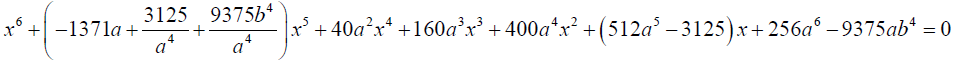
The factorized form of the sextic equation 13 is
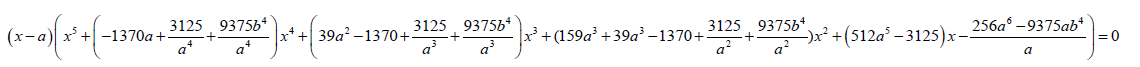
Solvable Factorized Forms
In chapter 2 we saw that higher degree polynomials are always reducible. It is still possible to identify ways of reducing higher degree polynomial to produce quadratic, cubic and even quartic factors [12].
In this paper I will discuss possible factorization forms to achieve this.
Consider the Bring-Jerrard quintic equation:
x5 + px + q = 0 (16)
For the Bring- Jerrard quintic equation the factorizations form:
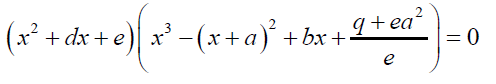 (17)
(17)
can be used to reduce the Bring-Jerrard quintic in general. In this form, the exogenous parameters can be related to endogenous parameters. That is:
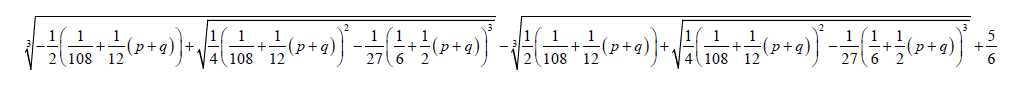 (18)
(18)
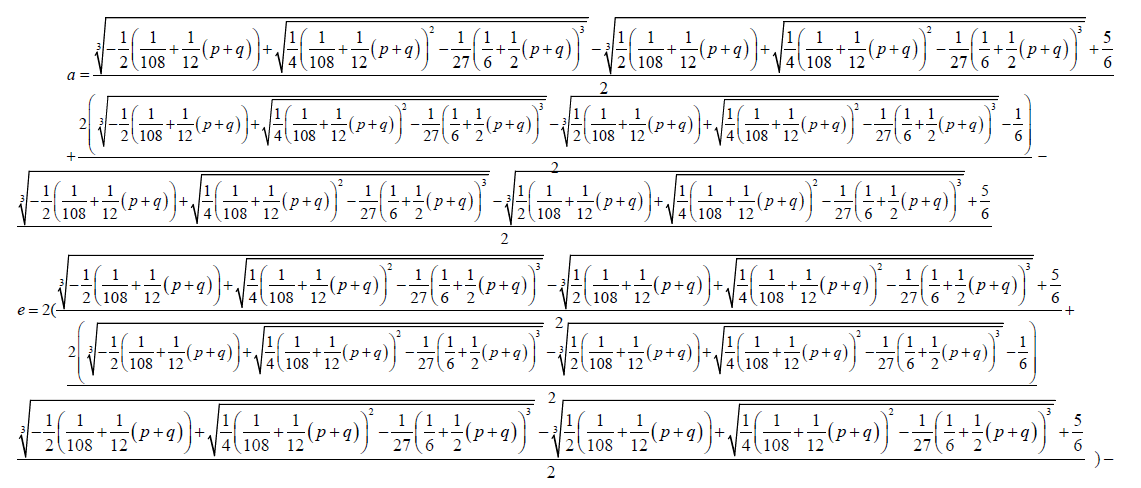 (19)
(19)
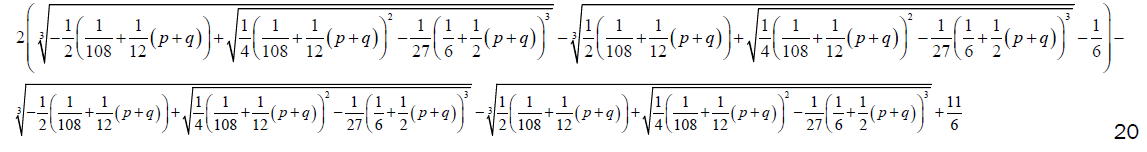 (20)
(20)
The Factorized form 0.2 of the Bring-Jerrard quintic equation is solved by substitution of the above coefficients in the auxiliary cubic and quadratic equations.
Two of the roots of the Bring-Jerrard quintic equations are;
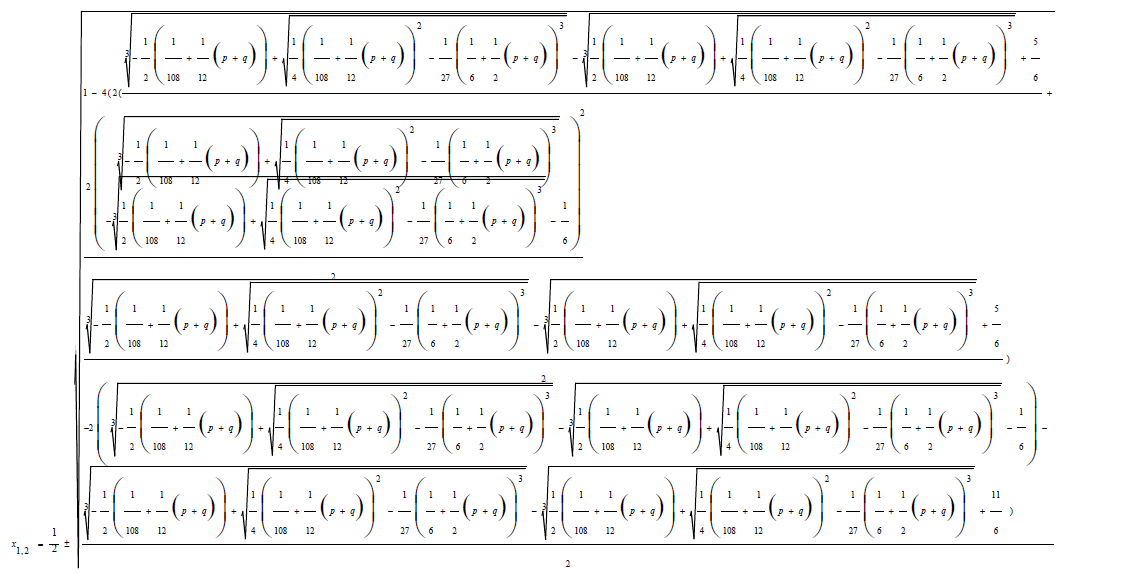 (21)
(21)
For sextic and septic equations the factorized form suggested below can be can be used be able to relate the endogenous and exogenous parameters and thus come up with their general solution:
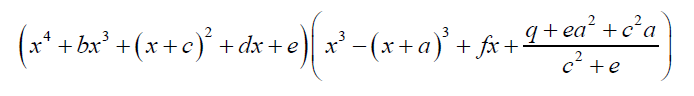 (22)
(22)
Conversion of Equation to Solvable Form
Consider the Bring Jerrard quintic equation:
x5 + px + q = 0 (23)
If we take p = kx3/2 (24)
The equation 0.1 takes the form:
x5 + kx5/2 + q = 0 (25)
In the form the roots of the quintic equation are:
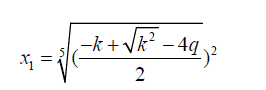 (26)
(26)
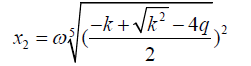 (27)
(27)
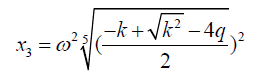 (28)
(28)
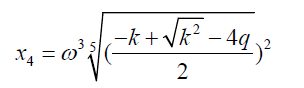 (29)
(29)
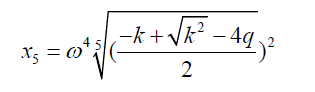 (30)
(30)
Where ω is the fifth root of unity.
Suppose we have a situation where the roots were obtained from say auxiliary quadratic equation after factorization, then the roots take the form:
L = f(p,q) (31)
where p and q are the parameters of the trinomial quintic equation
When L is equated to 0.5 and simplified we find out that:
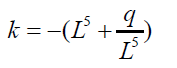 (32)
(32)
Substituting the equation 9 into 0.5 to 0.8 then we get the following results:
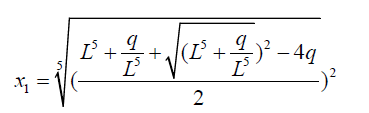 (33)
(33)
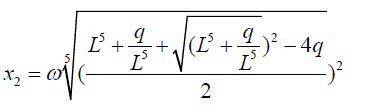 (34)
(34)
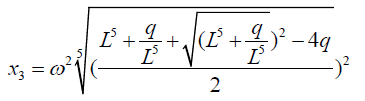 (35)
(35)
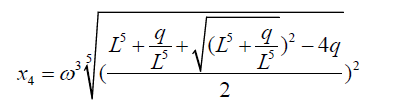 (36)
(36)
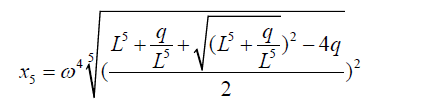 (37)
(37)
In the discussion in chapter 3.2 a value of L is given by:
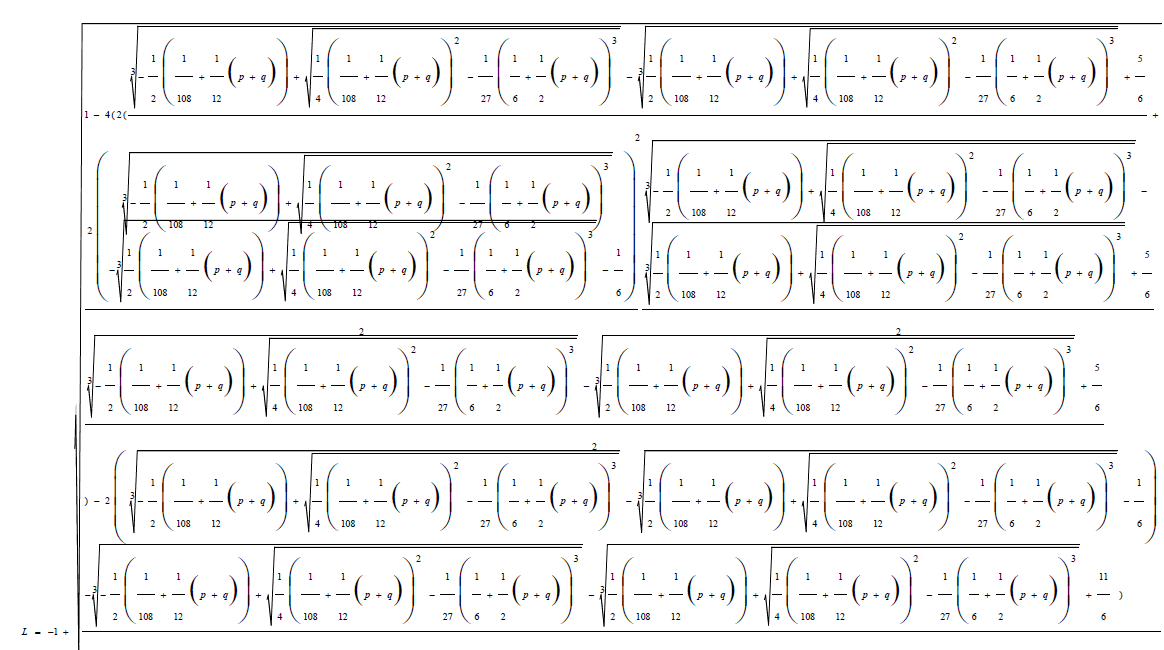 (38)
(38)
Thus the roots of the quintic equation are obtained by substituting the value of L in 1.6 into equations 1.1 to 1.5. The advantage of the above formulation is that it puts all polynomial equations under the same formula structure. I have used this example to illustrate with quintic equations but it can be extended to higher degree polynomials.
Summary Conclusion and Recommendations
There are a variety of techniques of solving algebraic equations of degrees greater than four degrees. The failure of the Lagrange and Galois resolvents to provide general algebraic solutions does not in any way mean that such solutions don’t exist. Abel – Ruffini impossibility theorem is incomplete in the sense that it did not exhaust all avenues of algebraic solution of higher degree polynomial. The proof was based on the limitations of the approaches used then. Galois Theory needs a fresh re-examination. There exists a framework under which formulae of polynomial equations of degree two and above take the same structural form. Abstract algebra needs a re-writing to enable other branches of mathematics and science that depend on it to grow.
I recommend an active research be initiated on solvability of higher degree polynomials.
I would like to express my since gratitude to the following: The Almighty God for making this piece of work successful. My wife for her Julie Ahadi encouragement and service.