ISSN: 2320-2459
ISSN: 2320-2459
New Mexico Institute of Mining and Technology, New Mexico, USA
Received Date: 04/09/2017; Accepted Date: 31/10/2017; Published Date: 07/11/2017
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Near the beginning of this work, applying beforehand the theory given here directly to astrophysical systems, we stated, “The force holding the astrophysical system known as a star together is gravitation. Deviation of astrophysical bodies from motion in a straight, or geodetic, line is either gravitational or non-existent. The astrophysical endeavour of observing astronomical systems to “prove” Einstein’s General Theory of Relativity is, according to the aforementioned works, a waste of time.” Adding, to the applications, those given in the body of this work, we argue herein that there is no change in any distance coordinate in a gravitational field, that the gravitational energy of motion of a mass arises from, conserving energy, the energy lost by the nested de Broglie wave clocks of the mass, that the density, incredibly, arbitrarily small for sufficiently large M, of the astrophysical object formerly known as a black hole depends inversely on the square of the mass M and is given by
General Relativity; Clock rate; Multiplicative inverse; Einstein tensor; De Broglie wave
With respect to the correctness of the arguments given herein, we mention here only that Einstein’s clock rate, given in The Foundation of the General Theory of Relativity, in a static gravitational field is that which we have given and that it is trivially greater than 1, the clock rate in flat space-time Figure 1:
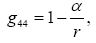
we have
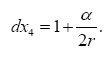
Thus the change in the clock in the gravitational field is greater than 1, the change of the clock in flat space-time; hence, Einstein actually obtains a faster clock in the gravitational field, contradicting the experimentally verified and claimed by Einstein slower clock. This consideration and those that follow, treated in greater detail in The Material Point Universe, give the blatantly obvious contradictions, which we seek, to the theory.
For the distance coordinate along a radius, Einstein’s result is that of a measuring rod that becomes longer, not shorter as he claims. The unit of length in such a measuring rod is greater than that where there is no gravitational field, and the measurement of a length, which has unit length in flat space-time, corresponds to the value that Einstein obtains.
In the case of the time coordinate, since
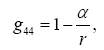 (1.1)
(1.1)
we have
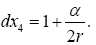 (1.2)
(1.2)
Thus the change in the clock in the gravitational field is greater than 1, the change of the clock in flat space-time; hence, Einstein actually obtains a faster clock in the gravitational field, contradicting the experimentally verified and claimed by Einstein slower clock. This consideration and those that follow, treated in greater detail in The Material Point Universe, give the blatantly obvious contradictions, which we seek, to the theory Figure 1.
For the distance coordinate along a radius, Einstein’s result is that of a measuring rod that becomes longer, not shorter as he claims. The unit of length in such a measuring rod is greater than that where there is no gravitational field, and the measurement of a length, which has unit length in flat space-time, corresponds to the value that Einstein obtains.
We give, herein, the machinery for the gravitational force. This undertaking, as usual, is on the fly, and includes sound arguments based on elementary concepts of space, time, and matter; so, in a sense, we do elementary, theoretical, experimental, and applicational physics. We thus state, beforehand, what we must do.
We characterize this work as a combination of original arguments and transcendent writing. Previous works, The Material Point Universe and The Material Point Universe Revisited, by this author on relativity were rejected by Classical and Quantum Gravity for the reason that they did not publish this type of article in any of their journals. The Astrophysical Journal rejected the same works for the reason that theoretical works must be applied to astrophysical systems: “Our journal specializes in manuscripts presenting new results on astronomical observations or theory applied directly to astrophysical systems.”
This, in part, explains why astrophysicists are so poor when it comes to theory. The force holding the astrophysical system known as a star together is gravitation. Deviation of astrophysical bodies from motion in a straight, or geodetic, line is either gravitational or non-existent. The astrophysical endeavor of observing astronomical systems to “prove” Einstein’s General Theory of Relativity is, according to the aforementioned works, a waste of time.
Like the down the street blond girl, whose love we may never know for sure, beautiful and smiling at us for the first time so that we nearly fall off the ledge, this work we may never know for certain.
The consideration, in The Material Point Universe Revisited, of the Michelson-Morley experiment and Einstein’s special relativity gives us insight into the mechanism for changes in space and time coordinates in the gravitational case as well as exposing Einstein’s false postulates and arguments, leading us to expect more of the same in the case of general relativity. We thus give the application of the contents of The Material Point Universe Revisited to the General Theory of Relativity and gravitation, the application of which to astrophysical systems we have given above.
As noted in The Material Point Universe, Einstein, in The Foundation of the General Theory of Relativity, states,
“It is not my purpose in this discussion to represent the general theory of relativity as a system that is as simple and logical as possible, and with the minimum number of axioms; but my main object is to develop the theory in such a way that the reader will feel that the path we have entered upon is psychologically the natural one, and that the underlying assumptions will seem to have the highest possible degree of security.”
Thus Einstein’s approach, as he states it, attempts what amounts to psychological “conditioning” as his principle objective.
The lengthy setup of Einstein’s theories in The Material Point Universe and The Material Point Universe Revisited was necessary for a rigorous consideration of Einstein’s development and statement, word for word, of the general theory of relativity and special relativity. Whether a particular journal of physics publishes rigorous works of physical thought was not a consideration [1].
We seek in this work the nature of being. We have no need for psychology. Arguing, as Einstein did, using postulates that were ultimately blatantly false, has no place in science. Claiming proof, as Einstein did, of relativity theories on the grounds that the theories implied results that were true and ignoring obvious evidence that proved the theories false has no place in science.
Yet acceptance of Einstein’s relativity theories is one consequence of the psychological manipulation, which is hardly ever first-hand since the theory itself is left to the theorists. Spokesmen, who are rare, for the theories may include, if we are lucky, the theorists or, in the worst case, psychologically duped clones who find no need to look at evidence contradicting the theories since, according to them, the theories have been proved.
When we send the papers and, subsequently, what amounts to the Bender’s rods example to James Binney, Professor of Physics and Head of the Peierls Centre for Theoretical Physics, Oxford University, Binney, referring to Bender’s rods, replies,
“Your fallacy lies in the statement "at a certain time t" an event happens. This presumes the absoluteness of time. Actually different observers assign different times to the same event. If you step outside of Einstein's framework in setting up the problem, it is to be expected that you arrive at a contradiction.
Really, there's nothing in the least puzzling about special relativity. Physics is full of puzzles, but special relativity isn't a good hunting ground for them once you grasp that every situation has to be broken down into a number of events, and that spacetime coordinates need to be assigned to these events using the correct formulae for transforming between frames.”
Thus, applying Binney’s response to Einstein’s relativity theories in general, giving logical arguments based on Einstein’s postulates constitutes stepping outside Einstein’s framework of psychological duping and contradictions are to be expected. On the other hand, we adhere to the sound arguments that we give and the conclusion that the contradictions imply the falsity of Einstein’s theories [2].
Logically, contradictions and the falsity of the theory are equivalent. Thus, contradictions are to be expected if and only if the theory is false. As if contradictions were puzzles, Binney asserts that “special relativity isn't a good hunting ground for” puzzles. What we have found, rather than puzzles, are contradictions and that makes the theory false.
Since p implies q is true whenever p is false, p implies q true and q true do not imply p is true; hence, a proposition or theory cannot be proved by it implying evidence that is true. Nevertheless, Einstein, not surprisingly, claims not just proof, but convincing proof, in Foundation, § 14. The Field Equations of Gravitation in the Absence of Matter, where Einstein states,
“These equations, which proceed by the method of pure mathematics, from the requirement of the general theory of relativity, give us, in combination with the equations of motion (46), to a first approximation Newton’s law of attraction, and to a second approximation the explanation of the motion of the perihelion of the planet Mercury discovered by Leverrier (as it remains after corrections for perturbation have been made). These facts must, in my opinion, be taken as a convincing proof of the correctness of the theory.”
As noted in Bender Goes to Oxford, retired academic Michael Bowler, as if precision of the results made them more convincing, states,
“Gravity has only been tested in fairly weak field limits. In this limit, deflection of light by the sun has been tested to somewhere around the 1% level. The various relativistic phenomena for close binaries have been tested with ever increasing precision with the Hulse-Taylor binary pulsar……… As far as both SR and GR are concerned, so far so good!”
If there is any question, given such “testing,” of how general relativity can be false, we cite evidence, given in The Material Point Universe, that contradicts it. If the theory were true, then the evidence should imply the theory; to the contrary, the evidence contradicts the theory since the actual evidence is not what the theory implies. If this is not clear, logically, if p implies q is true and q is false, then p is false.
Space-time coordinates are given by measuring rods and clocks located in the system under consideration. Measuring rods count units of length and clocks count units of time or seconds; in neither case do they count the size of the unit. In the scanned images, from The Foundation of the General Theory of Relativity, below, Einstein considers “a unit measure of length laid “parallel” to the axis of x” and a unit period of a unit clock in flat space-time and obtains the corresponding changes of length and time, dx and dx4, as measured in the gravitational field. Einstein, by considering unit changes in the measured quantities in flat space-time, wants the reader to fall into the psychological trap that the changes in the measured quantities in the gravitational field correspond directly to changes in the units. Obviously, this is not the case.
In the case of the time coordinate, since
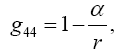 (1.3)
(1.3)
we have
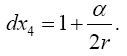 (1.4)
(1.4)
Thus the change in the clock in the gravitational field is greater than 1, the change of the clock in flat space-time; hence, Einstein actually obtains a faster clock in the gravitational field, contradicting the experimentally verified and claimed by Einstein slower clock. This consideration and those that follow, treated in greater detail in The Material Point Universe, give the blatantly obvious contradictions, which we seek, to the theory Figure 2.
For the distance coordinate along a radius, Einstein’s result is that of a measuring rod that becomes longer, not shorter as he claims. The unit of length in such a measuring rod is greater than that where there is no gravitational field, and the measurement of a length, which has unit length in flat space-time, corresponds to the value that Einstein obtains.
Einstein chooses, via approximations to the eqn. (46) in Figure 3 of the geodetic line, the elements of the “fundamental tensor”gμν so that
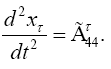 (1.5)
(1.5)
“As has already been mentioned more than once, the special theory of relativity as a special case of the general theory is characterized by the gμν having the constant values (4). From what has already been said, this means a complete neglect of the effects of gravitation. We arrive at a closer approximation to reality by considering the case where the gμν differ from the values of (4) by quantities which are small compared to 1, and neglecting small quantities of second and higher order. (First point of view of approximation.)
It is further to be assumed that in the space-time territory under consideration the gμν at spatial infinity, with a suitable choice of co-ordinates, tend toward the values (4); i.e. we are considering gravitational fields which may be regarded as being generated exclusively by matter in the finite region [3].
It might be thought these approximations must lead us to Newton’s theory. But to that end we still need to approximate the fundamental equations from a second point of view. We give our attention to the motion of a material point in accordance with the eqn. (46) in Figure 3. In the case of the special theory of relativity the components.
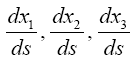
may take on any values. This signifies that any velocity
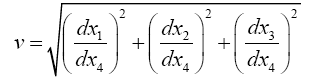
may occur, which is less than the velocity of light in vacuo. If we restrict ourselves to the case which almost exclusively offers itself to our experience, of v being small as compared with the velocity of light, this denotes that the components
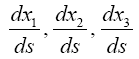
are to be treated as small quantities, while dx4/ds, to the second order of small quantities, is equal to one. (Second point of view of approximation.)
Now we remark that from the first point of view of approximation the magnitudes Γμν τ are all small magnitudes of at least the first order. A glance at eqn. (46) in Figure 3 thus shows that in this equation, from the second point of view of approximation, we have to consider only terms for which μ = ν = 4. Restricting ourselves to terms of lowest order we first obtain in place of (46) the equations
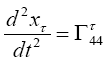
where we have set ds = dx4 = dt; or with restriction to terms which from the first point of view of approximation are of the first order:--
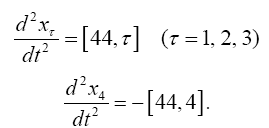
If in addition we suppose the gravitational field to be a quasi-static field, by confining ourselves to the case where the motion of matter generating the gravitational field is but slow (in comparison with the velocity of propagation of light), we may neglect on the right-hand side differentiations with respect to time in comparison with those with respect to the space co-ordinates, so that we have
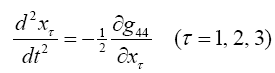
This is the equation of motion of the material point according to Newton’s theory, in which ½g44 plays the part of the gravitational potential. What is remarkable in this result is that the component g44 of the fundamental tensor alone defines, to a first approximation, the motion of the material point.”
So, if the significance of Einstein’s approximate space-time coordinates remains a puzzle, these are the approximate coordinates such that the coordinate acceleration, given by the eqn. (46) in Figure 3 of the geodetic line, along a radius is equal to −m / r2. In The Material Point Universe we stated,
“Einstein puts the acceleration of a material point to be the acceleration, given by the equation of the geodetic line, of a point xτ in the space-time coordinates assumed to exist by the theory. In § 21. Newton’s Theory as a First Approximation and § 22. Behaviour of Rods and Clocks in the Static Gravitational Field. Bending of Light-rays. Motion of the Perihelion of a Planetary Orbit from Foundation, Einstein places
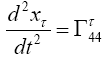 (1.6)
(1.6)
after approximating dxτ/dt with 0 for τ = 1, 2, 3, and 1 for τ = 4. (Once again, Einstein takes the time coordinate to be x4.) After approximating gττ with 1, Einstein obtains
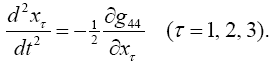
Einstein gives g44 by the equation
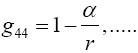 (1.7)
(1.7)
with α = 2m. Working backwards, this gives
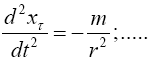 (1.8)
(1.8)
in fact, this equation shows that Einstein takes d2xτ/dt2 to be the observed acceleration. Apparently, via his approximations, he correctly puts Γ44τ = −m/r2. In fact, his value for g44 coincides with the value of g11 given by the Schwarzschild solution.”
Thus, Einstein claims that Newton’s law of attraction follows from the field equations in the absence of matter and the eqn. (46) in Figure 3 of motion. In two brief sections, § 13. Equations of Motion of a Material Point in the Gravitational Field. Expression for the Field-components of Gravitation and § 14. The Field Equations of Gravitation in the Absence of Matter, gives his explanation, i.e., clarification, of the nature of reality for the gravitational force; the motion of a material point is simply that of a point, which moves in a geodetic, a four-dimensional straight, line, the equation of motion for which is given by the equations of the geodetic line [4].
Thus, since we have shown above that “Einstein actually obtains a faster clock in the gravitational field, contradicting the experimentally verified and claimed by Einstein slower clock,” once again, quoting what we previously stated above, “the evidence contradicts the theory since the actual evidence is not what the theory implies. If this is not clear, logically, if p implies q is true and q is false, then p is false.”
For the sake of those “scientists” who need an experiment to verify what we claim, we point out that such experiments, which are repeatable, have been performed and that Einstein, no matter what he says, does not in fact obtain the experimentally verified coordinates for space-time coordinates. In lieu of discussing such experiments immediately, we note that the experimental results are, in a sense, mutually claimed (Figure 3).
For the sake of those “scientists” who need an explanation of how the theory can be false in the face of the theory uncannily implying such phenomena as gravitational attraction, the precession of the perihelion of the orbit of the planet Mercury, bending of light, and “various relativistic phenomena for close binaries,” we note that we have shown the notion of the theory giving Newton’s law of attraction to be false [5].
Thus, in the list of claims just given, we have taken out, i.e., shown to be false, the first of these on the grounds that the space-time coordinates, for which Einstein solves the equation of the geodetic line, are not the experimentally verified ones and are not what Einstein asserts they are.
So, for the sake of those scientists who need an explanation of how the theory can be false in the face of the theory uncannily implying the remaining three items on our list and not the first, we note that the theory is false if we remove the first claim pertaining to Newton’s law of attraction.
Moreover, to put this in perspective, we note that the other claims, each that the theory implies some experimentally verified relativistic phenomena, are considered to be true. Bowler, for example, without giving any arguments at all, asserts that the theory gives “various relativistic phenomena for close binaries.”
In The Material Point Universe, we gave other arguments, each of which proves the theory false, that we mention briefly here. The existence of singular material points or space-time singularities, e.g., black holes, implies that the space-time environment of a material point in a gravitational field is not what Einstein says it is and that one cannot simply ignore the space-time coordinates of the material point itself.
Moreover, the Einstein tensor, Gμν, which is a covariant tensor of the second rank, is the zero tensor. In Foundation, Einstein gives the law of transformation for such tensors Figure 4:
“Covariant Tensors.—On the other hand, if we take the sixteen products Aμν of the two covariant four-vectors Aμ and Bν,
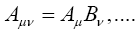 (1.9)
(1.9)
the law of transformation for these is
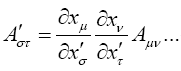 (1.10)
(1.10)
This law of transformation defines the covariant tensor of the second rank. All our previous remarks on contra variant tensors apply equally to covariant tensors.”
Now, the Einstein tensor, Gμν, has the value, given in §12. The Riemann-Christoffel Tensor from Foundation, as follows: “Contracting (43) with respect to the indices τ and ρ we obtain the covariant tensor of the second rank
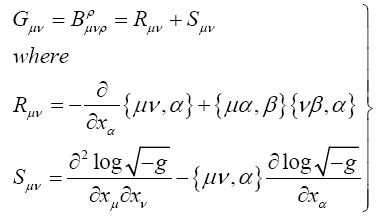
Note on the Choice of Co-ordinates.—It has already been observed in §8, in connexion with equation, that the choice of coordinates may with advantage be made so that √−g = 1. A glance at the equations obtained in the last two sections shows that by such a choice the laws of formation of tensors undergo an important simplification. This applies particularly to Gμν, the tensor just developed, which plays a fundamental part in the theory to be set forth [6]. For this specialization of the choice of co-ordinates brings about the vanishing of Sμν, so that the tensor Gμν reduces to Rμν.
On this account I shall hereafter give all relations in the simplified form which this specialization of the choice of co-ordinates brings with it. It will then be an easy matter to revert to the generally covariant equations, if this seems desirable in the special case.”
In The Material Point Universe, section 6, The equation of the geodetic line, we quote Einstein, from Foundation, as follows:
“Since the values of δxσ are arbitrary, it follows from this that
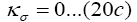
are the equations of the geodetic line.
If ds does not vanish along the geodetic line we may choose the “length of arc” s, measured along the geodetic line, for the parameter λ. Then w = 1, and in place of (1.10a) we obtain
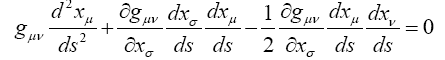
or, by a mere change of notation,
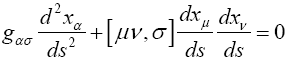
where, following Christoffel, we have written
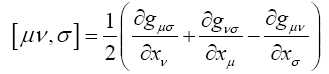
Finally, if we multiply (20d) by gστ (outer multiplication with respect to τ, inner with respect to σ), we obtain the equations of the geodetic line in the form
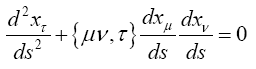
where, following Christoffel, we have set
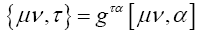
Thus, since
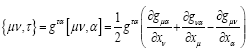 (1.14)
(1.14)
is defined or not, the Einstein tensor is either zero or undefined; and the Einstein tensor, if it is defined, is the zero tensor.
Regardless of this, Einstein, who, in effect, no longer has a theory, cheats once again. Einstein “finds” that the tensor Gμν is a function of the density of matter. In §16. The General Form of the Field Equations of Gravitation of Foundation, Einstein states,
“The field equations for the matter-free space formulated in §15 are to be compared with the field equation
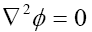
of Newton’s theory. We require the equation corresponding to Poisson’s equation
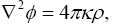
where ρ denotes the density of matter.
The special theory of relativity has led to the conclusion that inert mass is nothing more or less than energy, which finds its complete mathematical expression in a symmetrical tensor of second rank, the energy-tensor [7]. Thus in the general theory of relativity we must introduce a corresponding energy-tensor of matterTασ , which, like the energy components tσ of the gravitational field, will have a mixed character, but will pertain to a symmetrical covariant tensor.*
The system of equations shows how this energy-tensor (corresponding to the density ρ in Poisson’s equation) is to be introduced
into the field equations of gravitation. For if we consider a complete system (e.g. the solar system), the total mass of
the system, and therefore its total gravitating action as well, will depend on the total energy of the system, and therefore on the
ponderable energy as well as the gravitational energy. This will allow itself to be expressed by introducing into (51), in place of
the energy-components of the gravitational field alone, the sums 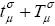 of the energy-components of matter and of gravitational
field. Thus instead of (51) we obtain the tensor equation
of the energy-components of matter and of gravitational
field. Thus instead of (51) we obtain the tensor equation
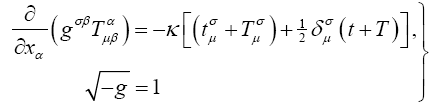
where we have set 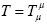 (Laue’s scalar). These are the required general field equations of gravitation in mixed form. Working
back from these, we have in place of (47)
(Laue’s scalar). These are the required general field equations of gravitation in mixed form. Working
back from these, we have in place of (47)
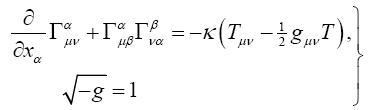
It must be admitted that this introduction of the energy-tensor of matter is not justified by the relativity postulate alone. For this reason we have here deduced it from the requirement that the energy of a gravitational field shall act gravitatively in the same way as any other kind of energy. But the strongest reason for the choice of these equations lies in their consequence that the equations of conservation of momentum and energy, corresponding exactly to equations, hold good for the components of the total energy. This will be shown in §17.”
In The Material Point Universe, we stated,
“In General Relativity, Wald writes:
“The basic framework of the theory of general relativity arises from considering the opposite possibility: that we cannot in principle – even by complicated procedures – construct inertial observers in the sense of special relativity and measure the gravitational force. This is accomplished by the following bold hypothesis: The space time metric is not flat, as was assumed in special relativity. The world lines of freely falling bodies in a gravitational field are simply the geodesics of the (curved) space time metric. In this way, the ‘background observers’ (geodesics of the space time metric) automatically coincide with what was previously viewed as motion in a gravitational field. As a result we have no meaningful way of describing gravity as a force field; rather, we are forced to view gravity as an aspect of space time structure. Although absolute gravitational force has no meaning, the relative gravitational force (i.e., tidal force) between two nearby points still has meaning and can be measured by observing the relative acceleration of two freely falling bodies. This relative acceleration is directly related to the curvature of space time by the geodesic deviation equation [8].”
Having given the ontology, Wald asserts that “the entire content of general relativity may be summarized as follows: Space time is a manifold M on which there is defined a Lorentz metric gab. The curvature of gab is related to the matter distribution in space time by Einstein’s equation.”
Having given the ontology, Wald asserts that “the entire content of general relativity may be summarized as follows: Space time is a manifold M on which there is defined a Lorentz metric gab. The curvature of gab is related to the matter distribution in space time by Einstein’s equation.”
Wald’s equation, which is Einstein’s equation and which Wald gives as
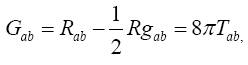 (1.15)
(1.15)
with 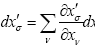 the stress-energy tensor, corresponds to Einstein’s equation, the General Form of the Field Equations of Gravitation. We, on the other hand, have proved that Gμν, and, hence, Tμν, is either zero or undefined.
the stress-energy tensor, corresponds to Einstein’s equation, the General Form of the Field Equations of Gravitation. We, on the other hand, have proved that Gμν, and, hence, Tμν, is either zero or undefined.
Einstein defines contravariant and covariant four vectors as follows:
” Contavariant Four-vectors.—The linear element is defined by the four ‘components’ dxν, for which the law of transformation is expressed by the equation
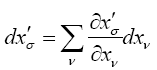
The dx'σ are expressed as linear and homogeneous functions of the dxν. Hence we may look upon these co-ordinate differentials as the components of a ‘tensor’ of the particular kind which we call a contravariant four-vector. Anything which is defined relatively to the system of co-ordinates by four quantities Aν, and which is transformed by the same law
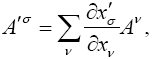
we also call a contravariant four-vector. From (5a) it follows at once that the sums Aσ ± Bσ are also components of a fourvector if Aσ and Bσ are such. Corresponding relations hold for all ‘tensors’ subsequently to be introduced. (Rule for the addition and subtraction of tensors.)
Covariant Four-vectors.—We call four quantities Aν the components of a covariant four-vector, if for any arbitrary choice of the contravariant four-vector Bν
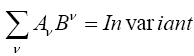
The law of transformation of a covariant four-vector follows from this definition. For if we replace Bν on the right-hand side of the equation
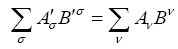
by the equation resulting from the inversion of (5a),
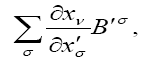
we obtain
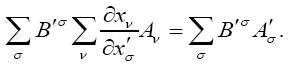
Since this equation is true for arbitrary values of the B'σ, it follows that the law of transformation is
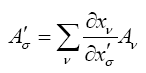
Note on a Simplified Way of Writing the Expressions.—A glance at the equations of this paragraph shows that there is always a summation with respect to the indices which occur twice under a sign of summation (e.g. the index ν in (5)), and only with respect to indices which occur twice. It is therefore possible, without loss of clearness, to omit the sign of summation. In its place we introduce the convention:—If an index occurs twice in one term of an expression, it is always to be summed unless the contrary is expressly stated [9].
The difference between covariant and contravariant four-vectors lies in the law of transformation ((7) or (5) respectively). Both forms are tensors in the sense of the general remark above. Therein lays their importance. Following Ricci and Levi-Civita, we denote the contravariant character by placing the index above, the covariant by placing it below.”
In §4. The Relation of the Four Co-ordinates to Measurement in Space and Time of Foundation, Einstein states, “For infinitely small four-dimensional regions the theory of relativity in the restricted sense is appropriate if the co-ordinates are suitably chosen.
For this purpose we must chose the acceleration of the infinitely small (“local”) system of co-ordinates so that no gravitational field occurs; this is possible for an infinitely small region. Let X1, X2, X3 be the co-ordinates of space and X4 the appertaining co-ordinate of time measured in the appropriate unit.* If a rigid rod is imagined to be given as the unit measure, the co-ordinates, the co-ordinates, with a given orientation of the system of co-ordinates, have a direct physical meaning in the sense of the special theory of relativity.
*The unit of time is chosen so that the velocity of light in vacuo as measured in the “local” system of co-ordinates is equal to unity.”
Einstein defines the magnitude of the linear element pertaining to points of the four-dimensional continuum in infinite proximity to be the ds such that
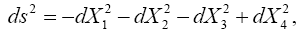
which Einstein asserts has, by the special theory of relativity, “a value which independent of the orientation of the local system of co-ordinates.”
Each differential dX 'μ has a unique representation
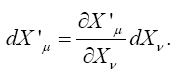
The invariance of a covariant tensor Aμ means that for any choice of the dXμ, we have
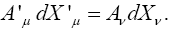
Similarly, for Aμν a covariant tensor of the second rank and any choice of the dXμ and dXν, we have
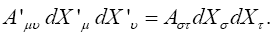
Suppose that for some system of coordinates X'1, X'2, X'3, X'4, the Einstein tensor G'μν is non-zero for some value of μ and ν at some point. Then for some choice of the dX 'μ and dX 'ν , we must have
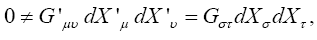
with 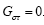 the Einstein tensor in flat space-time. This contradicts
the Einstein tensor in flat space-time. This contradicts 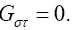
This last proof that the Einstein tensor is the zero tensor depends on the definition of covariance and the vanishing of the tensor in flat space-time; whereas, the previous proof depended on the law, which depends on the definition of covariance, of transformation of covariant tensors of the second rank and the vanishing of the tensor in flat space-time [10].
When we open the Chou, Wineland et al paper, starting with the part on clocks in a gravitational field, we find:
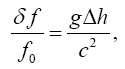 (2.1)
(2.1)
which is an approximation, is not equivalent to the change in the rate, according to The Foundation of the General Theory of Relativity, of a clock in a gravitational field Figure 5.
We receive, as an e-mail attachment from a recipient of an earlier version of this paper and the others, a copy of the 2010 paper, “Optical Clocks and Relativity,” by recent Nobel laureate David Wineland, C. W. Chou et al. In his first e-mail, without the attachment, the recipient writes,
“Darrell
I think you have a basic error in your understanding of the text you're quoting.
A region of space in which G_{mu,nu} = 0 represents a flat patch of space-time in which there is no curvature [11].
You could describe that same flat region of space in a different coordinate system via a transform of the type you've written out. It's then true to say that the same region of space will also have G'_{sigma,tau} = 0 when described in an alternative primed coordinate system. This has to be the case; if curvature is zero in one little patch of space, it should not matter which coordinate system is used to describe that patch.
You write: This is called the law of transformation for covariant tensors of the second rank. In the case of the Einstein tensor Gmn, which is zero in flat space-time, one can calculate its value in any other coordinate system by replacing the Amn in equation by 0 and summing over m,n. This makes the Einstein tensor the zero tensor in flat space-time (emphasis mine).
I'm not quite sure what your point is? You find that the curvature is zero independent of the coordinate system, as you should. That's not evidence that "Einstein" is "cheating". If you think it's evidence of "Einstein cheating" then it suggests you simply don't understand the subject matter.
It is quite a different statement to say that because G_{mu,nu} = 0 in a flat region, G'_{sigma,tau} would also have to be null in some separate region of space that instead contains a source of the gravitational field. The curvature tensor that describes a region of space containing a source of gravity should be inequivalent to the curvature tensor of flat space-time. We shouldn't be able to transform an arbitrary G'_{sigma,tau} into the tensor for flat space, since not all space is flat.
Moreover, there are plenty of experimental tests that confirm the predictions of special and general relativity. For instance, the recent Nobel Laurette David Wineland has measured time dilation over a height of approx. 1 meter in the lab, by comparing two atomic clocks accurate to one part in 10^-17. I think that his experimental evidence for special and general relativity (and many other works like it) trump your arguments. Go and read his paper, it's from 2010 and published in Science [12].
I don't see what you're going to achieve with your writing. Your writing contradicts results that have been experimentally demonstrated; the obvious conclusion is that you're in error. Why not direct your energies at something more useful?
Sincerely,
Spammed of Oxford”
In a subsequent e-mail, the one with the attachment, the recipient writes,
“Darrell
Whilst I admire your persistence, if you want to actually contribute to science through pursuing your current line of activity, please could you trouble yourself to enrol as a test subject in a study of neurodegenerative diseases? I am certain there will be neurologists out there (probably those specialising in Korsakoff's encephalopathy) who would be fascinated to investigate the organic brain damage you have evidently sustained, and the consequent delusions relating to Einstein and the like that you now express through your writing.
In that manner, you could continue to pen your missives whilst making a valid and worthwhile contribution to human knowledge.
Here's a report on some recent demonstration of some of the predictions of special and general relativity, if you're interested in informing yourself.
Sincerely,
Spammed of Oxford”
And finally, the recipient writes,
“Darrell
From the "Benders Rods" example it became apparent that you lack the capabilities of most undergraduates when it comes to solving text book problems on special relativity.
I think that to refute or add to special relativity or general relativity, it would bolster your case substantially to at least be competent with the subject.
Instead, you've demonstrated that you fail to understand or operate the mathematics required for analysis using special relativity, which you then describe as flawed. Forgive me for finding your arguments unconvincing.
If you can set out, side by side, an example worked through with "Standard" special relativity, and then your own slant on the matter, and show that the two systems of thought reach different conclusions for the same experiment, you could probably convince someone to try the experiment if it has not been done already, or more likely correct your attempt at the solution using "standard" special relativity.
As it stands, your arguments seem to lack any obvious testable hypothesis or refutability, and therefore fail the test of Karl Popper.
In terms of the return receipts, I suspect your emails are read out of morbid curiosity.
If you can manage to publish any of your writings in a peer reviewed journal, rather than the current vanity / spam press approach, if you can describe a testable difference in the conclusions of special relativity vs. Bender mechanics, people will read you and take you seriously; without that you're out in the wilderness.”
Before discussing the paper by Chou, Wineland et al, we note that for any point in a given coordinate system, the Einstein tensor Gμν has sixteen components, each of which is single valued, this value given by the law of transformation for covariant tensors of the second rank. Thus, the argument that, at a point in a given coordinate system, the values, as calculated by the law of transformation, of the components of the Einstein tensor vary with the initial region of space-time is nonsense [13].
When we open the Chou, Wineland et al paper, starting with the part on clocks in a gravitational field, we find:
Astonishingly, just five lines in, the equation
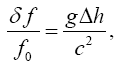 (2.2)
(2.2)
which is an approximation, is not equivalent to the change in the rate, according to The Foundation of the General Theory of Relativity, of a clock in a gravitational field. On the other hand, it is similar, if not identical, in form to the equation, arrived at, to a first approximation, via the principle of equivalence that Einstein gives in his 1911 paper, On the Influence of Gravitation on the Propagation of Light. If for no other reason, the equation from Influence holds only to a first approximation since g varies over the interval Δh. In addition to assuming the principle of equivalence, which states that a system of coordinates at rest in a homogeneous gravitation field is “physically exactly equivalent” to a uniformly accelerated, with the acceleration opposite to the direction of the lines of the gravitational force, system of coordinates in a space free of gravitational fields, Einstein assumes that the change, equal, to a first approximation, via the principle of equivalence, to the change, due to the Doppler effect, in the frequency of light arriving at a receiver after being emitted by an emitter in a uniformly accelerated system of coordinates, in frequency of light in the gravitational field is a result of clocks moving more slowly in the gravitational field. Thus, inserting the - sign since Δh is negative, the equation (Figure 5):
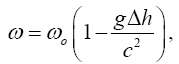 (2.3)
(2.3)
which gives, via the Doppler effect, the frequency ω of light reaching the receiver, with ω0 the frequency of light leaving the emitter, higher in the direction of acceleration than the receiver by a distance Δh, must hold, via the principle of equivalence, to a first approximation in the gravitational field. Performing the multiplication by ω0, subtracting ω0 from both sides, and dividing both sides by ω0, we obtain
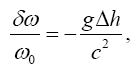 (2.4)
(2.4)
which, with the exception of the - sign, is virtually identical to the Chou, Wineland eqn. (2) in Figure 6 with the ω’s replaced with f’s.
Since the frequency of light is inversely proportional to the clock rate, we may write the first equation as
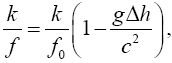 (2.5)
(2.5)
or
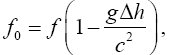 (2.6)
(2.6)
from which, to a first approximation, it follows that
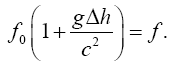 (2.7)
(2.7)
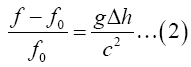 (2.8)
(2.8)
This last equation applies to clocks with f0 corresponding to the rate of the higher clock and f the rate of the lower clock; thus,
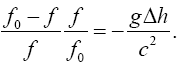 (2.9)
(2.9)
Interchanging f and f0 and replacing -Δh with Δh, we obtain, with orientation of the clocks as in the Chou, Wineland paper,
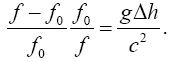 (2.10)
(2.10)
Now, since
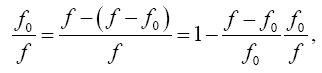 (2.11)
(2.11)
we have
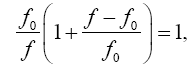 (2.12)
(2.12)
or, to a first approximation,
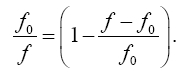 (2.13)
(2.13)
Thus
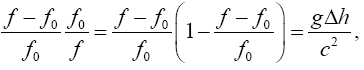 (2.14)
(2.14)
or, to a first approximation,
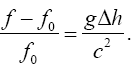 (2.15)
(2.15)
Thus, we have shown that the equation, which Chou, Wineland verify, follows from Einstein’s result from Influence. We assumed,
along the way, those certain quantities, such as 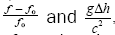 are “small.” Had we chosen the reverse position of the
emitter and receiver with the light moving in the direction of acceleration, we should have arrived at the identical result, using the
Doppler effect and the principle of equivalence arguments, in the same steps up to eqn. (2) in Figure 6. The equation
are “small.” Had we chosen the reverse position of the
emitter and receiver with the light moving in the direction of acceleration, we should have arrived at the identical result, using the
Doppler effect and the principle of equivalence arguments, in the same steps up to eqn. (2) in Figure 6. The equation
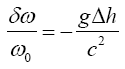 (2.16)
(2.16)
becomes, replacing h with r and taking the limit as Δr → 0, a differential equation
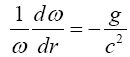 (2.17)
(2.17)
in ω and r. In effect, we have shown that the left-side derivative is equal to the right-side derivative.
For a differentiable function f of x, the function 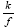 has the derivative (Figure 6):
has the derivative (Figure 6):
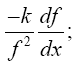 (2.18)
(2.18)
hence,
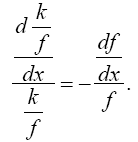 (2.19)
(2.19)
Thus, we have proved, to a first approximation at least, that
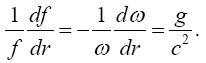 (2.20)
(2.20)
It remains to show that, for Einstein’s clock frequency in Foundation (Figure 1),
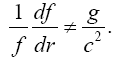 (2.21)
(2.21)
Einstein obtains (eqn. (70) in Figure 7) for g44 the value:
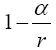 (2.22)
(2.22)
with
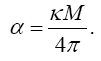 (2.23)
(2.23)
For a “unit clock” at rest in a static gravitational field, corresponding to the “clock period” or time interval ds = 1 in the “local”system of coordinates, Einstein obtains, by the invariance of ds2
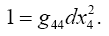 (2.24)
(2.24)
More generally, for ds = dt and x4 = t′, we have
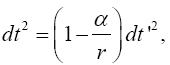 (2.25)
(2.25)
or
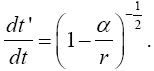 (2.26)
(2.26)
Thus, according to Foundation, this last equation gives, to at least a first approximation, the instantaneous clock rate for a
clock in a gravitational field. The derivative 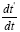 is just f, the clock frequency in the gravitational field (Figure 7).
is just f, the clock frequency in the gravitational field (Figure 7).
Simply by inspection, we already know that this clock rate is greater than 1, the clock rate in the “local” system; so, this gives the clock rate of a faster clock. Once again, for dt = ds = 1 in the local system, Einstein obtains this:
For average undergraduate students, every one of whom is better than Bender at mathematics, it is the last line (Figure 1):
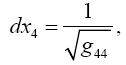 (2.27)
(2.27)
with
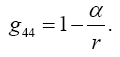 (2.28)
(2.28)
By the chain rule and since the unit of time is chosen so that , C=1 we thus have
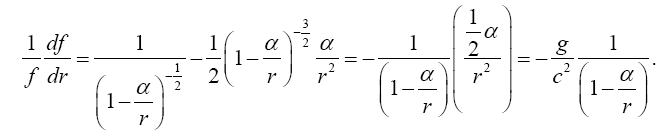 (2.29)
(2.29)
This is obviously not, the problem being the sign,
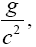 (2.30)
(2.30)
the value of
 (2.31)
(2.31)
according to the Chou, Wineland paper.
Should there be any question with respect to which system of coordinates is that in the gravitational field, please refer to the above (Figure 8). It is the dxμ that are the “differentials of the four-dimensional co-ordinates of any chosen system of reference,” i.e., the system of coordinates at rest in the gravitational field. It is the “local” system of coordinates that is the system for which the acceleration is chosen “so that no gravitational field occurs.”
Since
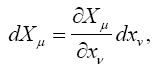 (2.32)
(2.32)
we have
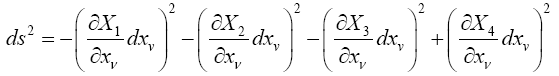
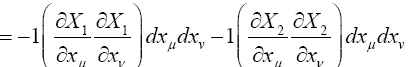
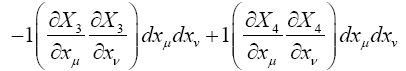
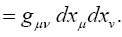 (2.33)
(2.33)
If it were not clear, ds2 and, hence, ds are defined in the local system of coordinates, where the gμν have the constant values given by (Figure 9):
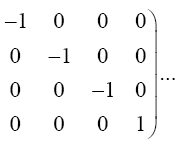 (2.34)
(2.34)
In “any chosen system of reference,” by the unique representation of the differentials
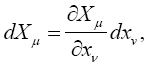 (2.35)
(2.35)
we have
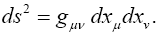 (2.36)
(2.36)
Now, if we consider the clock rate f' if g44 is the multiplicative inverse, i.e.,
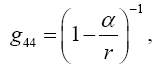 (2.37)
(2.37)
of Einstein’s value, by our previous result we have
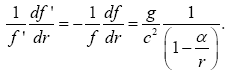 (2.38)
(2.38)
It is this last equation, tempting in that it gives other terms than just the one in the equation, resulting from the equivalence
principle, that Chou, Wineland et al use, without any apparent suspicion by any undergraduate student, and in that it has the right
sign for the value of 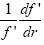 , and the time coordinate that goes with it that we consider for the correct result.
, and the time coordinate that goes with it that we consider for the correct result.
So, if we assume that a material point moves in a geodetic line in some region, there is always a region of flat space-time for which the same line is a geodetic line. In any other non-accelerated coordinate system, the same straight line is a geodetic line. Thus, assuming that a material point moves in a geodetic line in the first place and that the coordinate acceleration is equal to the acceleration of the material point, Einstein’s solution gives a material point that moves in a geodetic line with acceleration –m/r2. Unfortunately for Einstein, as we have shown in numerous ways, these are not the correct coordinates [14].
This assumption, that the coordinate acceleration is equal to the acceleration of the material point, may at first seem correct; but, the implied coordinates are not the actual ones and, hence, the relativity of the given accelerations requires more thought. If we consider the motion of the material point to be such that its acceleration is the opposite of the coordinate acceleration, the value of which is m/r2, then, if we assume that the material point has a constant velocity along the geodetic line, we obtain –m/r2 for the acceleration, with respect to its coordinates in the gravitational field, of the material point and, as we need to show, spacetime coordinates that equal the experimental ones.
At the beginning of the April 22, 1966 article “Relativity: Proving Einstein Right” in Time magazine, the author states,
“"The chief attraction of the theory lies in its logical completeness," wrote Albert Einstein after publishing his general theory of relativity in 1915.”If a single one of the conclusions drawn from it proves to be wrong, it must be given up; to modify it without destroying the whole structure seems to be impossible."”
This claim of logical completeness, which is essentially meaningless, comes from the same Einstein who wrote this:
Now, having almost trivially shown that every result that we have considered of the theory is false, we realize that this statement by Einstein of logical completeness is just part of his psychological nonsense; yet, the psychological trap is so strong and mystifying that we must fight the overwhelming mind set best expressed by “But it’s still true, right?” (Figure 9).
Immediately after the “…but my main object is to develop the theory in such a way that the reader will feel that the path we have entered upon is psychologically the natural one, and that the underlying assumptions will seem to have the highest possible degree of security” statement, Einstein requests, “With this aim in view let it now be granted that :—
For infinitely small four-dimensional regions the theory of relativity in the restricted sense is appropriate, if the co-ordinates are suitably chosen.” In effect, Einstein is saying, “give me this.”
To this end, Einstein assumes that the acceleration of the “local system of coordinates is chosen so that no gravitational field occurs;” i.e., the acceleration of the local system of coordinates equals that of the material point. In fact, we can do better than that: we can choose the motion of the local system of coordinates so that it matches the motion of the material point (Figure 3).
In this local system of coordinates, which we may as well consider since any motion of the material point is not attributable to the gravitational field, the material point does not move in a four-dimensional straight line; it does not move at all [15]. The equation of the geodetic line does not give the motion of the material point in the local system since, once again, it does not move. Even in Einstein’s “local” system of coordinates, the material point does not move since this local system is infinitely small.
Yet, obliviously, Einstein asserts that “with respect to K0 the law of motion corresponds to a four-dimensional straight line, i.e., to a geodetic line,” and by the definition, independent of the coordinate system, of the geodetic line, concludes that the equation of the geodetic line gives the motion of the material point in the gravitational field; and that even when there is no such system of reference K0, the assumption “readily suggests itself” that it remains true. Once again, to clear this up, there is never such a system of reference K0. Einstein states, “With this aim in view let it now be granted that :—,” so “that the reader will feel that the path we have entered upon is psychologically the natural one, and that the underlying assumptions will seem to have the highest possible degree of security.” Einstein’s psychological manipulation is that quick, the economy of motion apparent or “as plain as the nose on your face.”
If in the gravitational field, a material point moves in a geodetic line, the only acceleration is arguably in the coordinates of a system at rest in the gravitational field. It is in this system that the acceleration, which we experience in the gravitational field, is observed and measured. What we really want, perhaps, in contrast to Einstein’s hypothesis that the coordinate acceleration is equal to the acceleration of the material point, is for the coordinate acceleration to be the opposite or additive inverse of the acceleration of the material point.
For the correct coordinates, we must perceive and measure the acceleration of the material point as –m/r2; moreover, the correct coordinates must be the experimentally verified ones. We can always assume that a material point moves in a geodetic line [16]. Once again, if it were not clear, ds2 and, hence, ds are defined in the local system of coordinates, where the gμν have the constant values given by
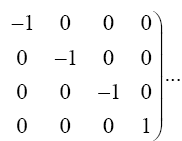 (3.1)
(3.1)
More generally, we may as well define ds2 and, hence, ds in some finite or, perhaps, infinite region, which we call flat spacetime, where the gμν have the constant values just given. We have, of course, by definition
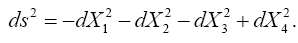 (3.2)
(3.2)
So, if we assume that a material point moves in a geodetic line in some region, there is always a region of flat space-time for which the same line is a geodetic line. In any other non-accelerated coordinate system, the same straight line is a geodetic line. Thus, assuming that a material point moves in a geodetic line in the first place and that the coordinate acceleration is equal to the acceleration of the material point, Einstein’s solution gives a material point that moves in a geodetic line with acceleration –m/r2. Unfortunately for Einstein, as we have shown in numerous ways, these are not the correct coordinates.
This assumption, that the coordinate acceleration is equal to the acceleration of the material point, may at first seem correct; but, the implied coordinates are not the actual ones and, hence, the relativity of the given accelerations requires more thought. If we consider the motion of the material point to be such that its acceleration is the opposite of the coordinate acceleration, the value of which is m/r2, then, if we assume that the material point has a constant velocity along the geodetic line, we obtain –m/r2 for the acceleration, with respect to its coordinates in the gravitational field, of the material point and, as we need to show, spacetime coordinates that equal the experimental ones.
Now, the apparent silliness of assuming that acceleration of the material point is the opposite of the coordinate acceleration nearly led us to reject the assumption on the grounds that, after all, the material point must accelerate exactly like a coordinate point; but, on the other hand, we have already shown that the equality of the acceleration of the material point and the coordinate acceleration is false. The condition that, with or without the gravitational field, the material point is not accelerating at all in flat space-time has a precedent in the assertion, by Einstein in his 1911 paper On the Influence of Gravitation on the Propagation of Light, that the frequency of light moving in the direction of a mass changes exclusively because clocks in the gravitational field move more slowly by a factor inversely proportional to the corresponding factor giving the change in the frequency of light [16].
The Schwarzschild solution is described, after its derivation, by Wald in General Relativity as “the general solution, first discovered by Schwarzschild, of the vacuum Einstein equation for static, spherically symmetric space times.” The vacuum Einstein equation is Einstein’s “field equations in the absence of matter:”
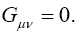 (3.3)
(3.3)
Now, we all know that Einstein solved the equation of the geodetic line and not the field equations in the absence of matter to obtain his “approximate” space-time coordinates. In The Material Point Universe, we showed that the Schwarzschild solution is the solution of the equation of the geodetic line such that
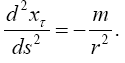 (3.4)
(3.4)
Keeping in mind that Einstein approximates ds with dt and that Wald’s ds2 is -ds2 where ds′ is Einstein’s ds, the above equation follows from the result from Universe:
“The Schwarzschild solution in spherical coordinates is given by
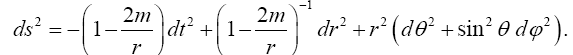
The metric ds2, called the metric of spacetime by Wald, has signature, the number of + and − signs occurring, − + + +, the inverse of Einstein’s metric. Metrics with this signature are referred to as Lorentzian (Figure 10).
Derivations of the Schwarzschild solution are in Gravitation, General Relativity, and Feynman Lectures on Gravitation. In General Relativity, m is M, which Wald calls the total mass. Feynman calls the total mass times Newton’s gravitational constant m; by a change in scale, these amounts to the same thing.
The intent here is to calculate d2xτ/dt2using the equation of the geodetic line. To that end, we lay the xτ axis along any radius. Evidently, along this axis, we have gμν= 0 for μ ≠ ν, and gμν= 1/gμν for μ = ν. In particular, we have g11= −(1−2m/r), gττ=(1−2m/r)−1, and gσσ= 1 for σ ≠ τ. We obtain
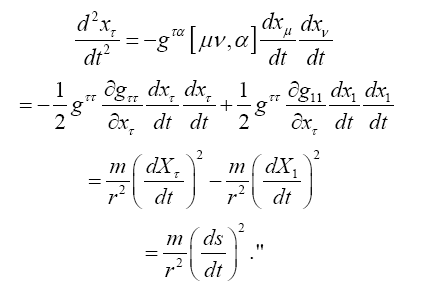
Now if we invert g11 and gττ so that 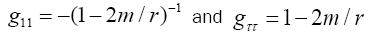 and leave the other gμν unchanged, we
obtain
and leave the other gμν unchanged, we
obtain
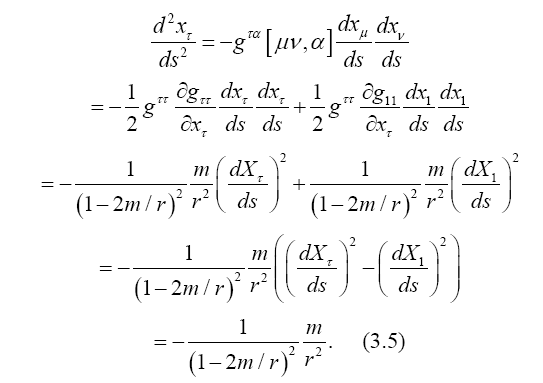
Once again, these calculations of 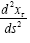 are for ds2 equal to - ds′2 where ds′ is Einstein’s ds
are for ds2 equal to - ds′2 where ds′ is Einstein’s ds
“As was previously discussed in section 4.4a, in the slow motion, weak field limit, the predictions of general relativity reduce to those of the Newtonian theory. However, the Schwarzschild solution, which describes the exact exterior field of a spherical body, predicts tiny departures from the Newtonian theory for the motion of planets in our solar system, and, in addition, predicts the “bending of light,” the gravitational redshift of light., and “time delay” effects. These four predictions have been accurately confirmed by precise measurements [17]. Indeed, except for the binary pulsar measurements (see the end of chapter 4), the predictions of the Schwarzschild solution in the weak field regime of our solar system are the only predictions of general relativity to have been tested in a quantitatively precise manner.”
Wald’s six-page “derivation” of the Schwarzschild solution of Einstein’s equation in section 6.1 compares lengthily to the four-step derivation of the Schwarzschild solution of the equation of the geodetic line such that
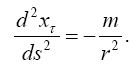 (3.6)
(3.6)
Wald’s derivation includes the substitution of a “trial solution,” which, of course, leads to the Schwarzschild solution; Wald states, “Since we have found no inconsistency, this means that our trial solution (generated by the initial guess ωb02 = ωb03 =0) is, in fact, the solution.”
Wald completely ignores Einstein’s theory of the motion, the acceleration being equal to the coordinate acceleration, of a material point in a gravitational field. Just by inspection, the time coordinate of the Schwarzschild solution corresponds to that of a faster clock; and Wald, obliviously, claims the theory predicts the gravitational redshift, which requires a slower clock, of light. The Chou, Wineland experiment tested Einstein’s prediction of clock rate from On the Influence of Gravitation on the Propagation of Light and not the clock rate from Foundation.
Setting 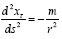 automatically introduces Newtonian theory into general relativity as an approximation; the second derivative
is with respect to s and not t. Einstein contrived the theory to give Newton’s theory as an approximation; Einstein failed to contrive
the theory enough to give the correct space-time coordinates. The idea, arguably attributable to Einstein, that a material point
moves in a geodetic line in a gravitational field has its roots in the equivalence principle and Einstein’s argument that the change
in frequency of light moving toward a mass was entirely due to clocks moving more slowly in the gravitational field (Figure 11).
automatically introduces Newtonian theory into general relativity as an approximation; the second derivative
is with respect to s and not t. Einstein contrived the theory to give Newton’s theory as an approximation; Einstein failed to contrive
the theory enough to give the correct space-time coordinates. The idea, arguably attributable to Einstein, that a material point
moves in a geodetic line in a gravitational field has its roots in the equivalence principle and Einstein’s argument that the change
in frequency of light moving toward a mass was entirely due to clocks moving more slowly in the gravitational field (Figure 11).
We have yet to consider, given Einstein’s space-time coordinates or the ones in which the gμμ’s are inverted, the motion, which one measures using these coordinates, of a material point. As we must give this matter the required thought, we first consider the “bending of light” in a gravitational field.
Einstein, without any arguments, remarks, “We easily recognize that the course of the light-rays must be bent with regard to the system of co-ordinates, if the gμν are not constant.” In what amounts to assuming, similar to assuming, before now shown to be false, that the acceleration of the material point is equal to the coordinate acceleration, in general that the coordinate-wise functions of the path of the light do whatever the corresponding functions of the coordinates do, Einstein assumes, specifically here, that the curvature of the light-ray is given by
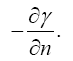 (4.1)
(4.1)
Taking the path of light to be parallel to the x2 -axis and perpendicular to the x1 -axis, which lies along a radius, Einstein obtains, with γ obviously less than 1 and decreasing in absolute value as r decreases with x2= r,
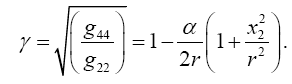 (4.2)
(4.2)
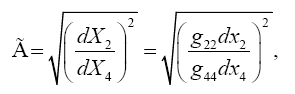 (4.3)
(4.3)
or
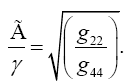 (4.4)
(4.4)
Thus, if we take the curvature of the path of the light ray to be
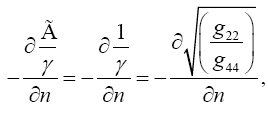 (4.5)
(4.5)
it is obvious how Einstein, with each gμμ the multiplicative inverse of what we for now consider its proper value, obtains what is apparently the correct result with the wrong gμμ’s.
Before considering bending of light in a gravitational field, we demonstrate how quickly one can move a gμμ from one side of an equation to the other. Suppose, as with the Schwarzschild solution, the non-diagonal gμν vanish so that, with the xτ axis aligned with a radius, we have, choosing the path from some xτ such that only the time coordinate varies,
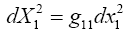 (4.6)
(4.6)
Thus
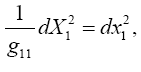 (4.7)
(4.7)
or
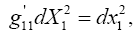 (4.8)
(4.8)
where
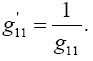 (4.9)
(4.9)
We note that eqn. (2) in Figure 6 is just eqn. (1) with g11 inverted and the dx1’s interchanged. Since the expression for dx12 is not the same as the expression for dx12, this is a counterexample/example to the assertions that all equations that hold in some coordinate system hold good for all systems of coordinates/are not laws of nature.
In The Material Point Universe, we quoted Einstein, from Foundation, on the general postulate of relativity or the postulate of general relativity as follows:
“We therefore reach this result: -- In the general theory of relativity, space and time cannot be defined in such a way that differences of the spatial co-ordinates can be directly measured by a unit measuring-rod or the differences in the time co-ordinate by a standard clock.
The method hitherto employed for laying co-ordinates into the space-time continuum in a definite manner thus breaks down, and there seems no other way which would allow us adapt systems of co-ordinates to the four-dimensional universe so that we might expect from their application a particularly simple formulation of the laws of nature. So there is nothing for it but to regard all imaginable systems of co-ordinates, on principle, as equally suitable for the description of nature. This comes to requiring that: --
The general laws of nature are to be expressed by equations which hold good for all systems of co-ordinates, that is, are covariant with respect to any substitutions whatever (generally co-variant).
It is clear that a physical theory which satisfies this postulate will also be suitable for the general postulate of relativity. For the sum of all substitutions in any case includes those which correspond to all relative motions of three-dimensional systems of co-ordinates. That this requirement of general co-variance, which takes away from space and time the last remnant of physical objectivity, is a natural one will be seen from the following reflexion. All our space-time verifications invariably amount to a determination of space-time coincidences. If, for example, events consisted merely in the motion of material points, then ultimately nothing would be observable but the meetings of two or more of these points [18]. Moreover, the results of our measuring are nothing but verifications of such meetings of the material points of our measuring instruments with other material points, coincidences between the hands of a clock and points of the clock dial, and observed point-events happening at the same place at the same time.”
So, eqns. (1) and (2) are not the same equation, but they are equivalent and one can obtain identical equations by replacing g'11 in (2) with g11 and interchanging the dx1’s; or, if we set
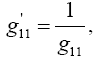 (4.10)
(4.10)
so that
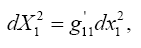 (4.11)
(4.11)
we obtain eqn. (1) in Figure 8 from eqn. (2) in Figure 6 by interchanging the dx1’s.
In Einstein’s consideration, which follows after these remarks, of the bending of the path of light, Einstein begins by claiming, by the special theory of relativity, that
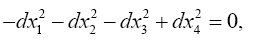 (4.12)
(4.12)
which, since the dxi dxi ’s are in the gravitational field, is to say that the velocity of light is equal to 1 in the static gravitational field even though the special theory of relativity has no bearing on the gravitational field; moreover, a quick glance at the Schwarzschild solution shows almost trivially that this is false. The assertion, in the remainder of Einstein’s first sentence, that the velocity of light is given “therefore by the general theory of relativity by equation” (73) confuses, once again, the location of the dxi’s.
Defining, in the sense of Euclidean geometry,
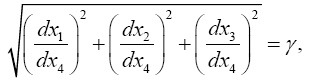 (4.13)
(4.13)
Einstein, without any arguments, remarks, “We easily recognize that the course of the light-rays must be bent with regard to the system of co-ordinates, if the gμν are not constant.” In what amounts to assuming, similar to assuming, before now shown to be false, that the acceleration of the material point is equal to the coordinate acceleration, in general that the coordinate-wise functions of the path of the light do whatever the corresponding functions of the coordinates do, Einstein assumes, specifically here, that the curvature of the light-ray is given by
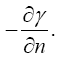 (4.14)
(4.14)
Taking the path of light to be parallel to the x2 -axis and perpendicular to the x1 -axis, which lies along a radius, Einstein obtains, with γ obviously less than 1 and decreasing in absolute value as r decreases with x2 = r,
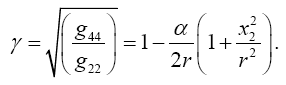 (4.15)
(4.15)
In flat space-time, with the coordinate axes aligned with the corresponding axes in the gravitational field, we have, for the velocity of light Γ,
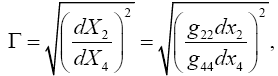 (4.16)
(4.16)
or
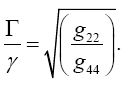 (4.17)
(4.17)
Thus, if we take the curvature of the path of the light ray to be
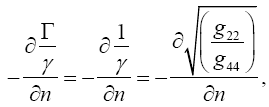 (4.18)
(4.18)
it is obvious how Einstein, with each gμμ the multiplicative inverse of what we for now consider its proper value, obtains what is apparently the correct result with the wrong gμμ’s.
Einstein’s consideration, from Foundation, of the bending of the path of light in a gravitational field follows:
“We now examine the course of light-rays in the static gravitational field. By the special theory of relativity the velocity of light is given by the equation
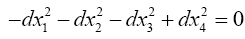
and therefore by the general theory of relativity by the equation
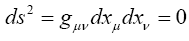
If the direction, i.e. the ratio dx1 : dx2 : dx3 is given, eqn. (7) in Figure 2 gives the quantities
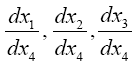
and accordingly the velocity defined in the sense of Euclidean geometry. We easily recognize that the course of the lightrays must be bent with regard to the system of co-ordinates, if the gμν are not constant. If n is a direction perpendicular to the propagation of light, the Huyghens principle shows that the light-ray, envisaged in the plane (γ, n), has the curvature − δγ/δn
We examine the curvature undergone by a ray of light passing by a mass M at the distance Δ. If we choose the system of co-ordinates in agreement with the accompanying diagram, the total bending of the ray (calculated positively if concave towards the origin) is given in sufficient approximation by.
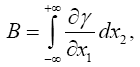
while (73) and (70) give
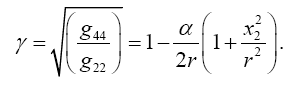
Carrying out the calculation, this gives
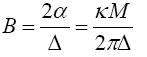
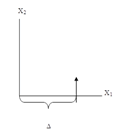
According to this, a ray of light going past the sun undergoes a deflexion of 1˙7"; and a ray going past the planet Jupiter a deflexion of about ˙02".”
In Part 3, we considered the Schwarzschild coordinates as a solution of the equation of the geodetic line such that the coordinate acceleration is equal to –m / r2; in Part 4, the bending of the path of light in a gravitational field. According to the general theory of relativity, the space-time coordinates, which are single-valued at each point, determine the motions of both the material point and the photon. We have yet to consider whether a material point moves in a geodetic line in a gravitational field.
If the path in space of a material point is not along a radius, then its path in space is not straight, but curved. Since ds is nonzero along such a path, the equation of the geodetic line applies, and the non-straightness of the line implies it is not a geodetic. In the case of a photon with non-radial path in space, its path in space is curved as well. In the case of the material point, we attribute the curved path to the path in space crossing radial lines, for which the ratios of the dXi in flat space-time differ. Since non-radial paths are not geodetics, we need only consider whether radial paths of material points are geodetics [4].
If a material point moves in a geodetic line along radial paths in space, then its motion has a stop/start character in flat
space-time if one catches and releases it in addition to moving at a constant velocity 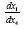 if the X1 axis is aligned along the radial
path.
if the X1 axis is aligned along the radial
path.
Einstein, of course, assumes that material points have geodetic lines as paths since that behavior of their motion “readily suggests itself.” Einstein, claiming proof on the basis of verification of certain implications of the theory, considers not a single point of what we have written in these first fifty pages. Metaphorically, the fat lady is ready to sing and the removal of the furniture is at hand.
If the positive X1 axis is aligned along a radius, X1 increasing with increasing r, and the x1 and x4 axes in the gravitational
field are aligned with the corresponding axes in flat space-time, we have, for the velocity 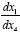 of the material point in the gravitational
field,
of the material point in the gravitational
field,
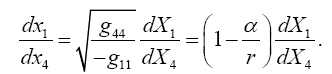 (5.1)
(5.1)
We note that there is no square-root in the expression on the right. By elementary functional analysis, the expression 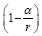 ,
which is the ratio of the velocity of the material point in the gravitational field to the velocity of the material point in flat space-time,
decreases as rdecreases. This contradicts the acceleration, an increase in the absolute value of the velocity, of the material point
in the gravitational field as r decreases.
,
which is the ratio of the velocity of the material point in the gravitational field to the velocity of the material point in flat space-time,
decreases as rdecreases. This contradicts the acceleration, an increase in the absolute value of the velocity, of the material point
in the gravitational field as r decreases.
Thus, we have proved that if a material point moves in a geodetic line, it does not do it with Einstein’s space-time coordinates,
which we have previously shown to be incorrect. According to Einstein’s theory, the expression 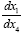 must correspond to the
measured velocity of the material point in the gravitational field.
must correspond to the
measured velocity of the material point in the gravitational field.
If we consider the acceleration, 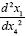 , which must equal the measured acceleration in the gravitational field, we have, once
again, by the chain rule,
, which must equal the measured acceleration in the gravitational field, we have, once
again, by the chain rule,
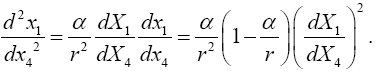
This last expression is positive, which is the wrong sign, and in order for the first order approximation to be 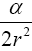 , which is the absolute value of the measured acceleration due to gravity, we must have
, which is the absolute value of the measured acceleration due to gravity, we must have
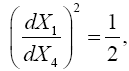 (5.3)
(5.3)
or
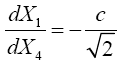 (5.4)
(5.4)
since the unit of time is chosen so that the velocity of light is equal to one.
Just giving the rule, as Einstein attempted to do by asserting that a material point moves in a geodetic line and that the
coordinate acceleration, given by the equation of the geodetic line, is equal to 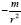 , determining the motion of a material point in a
gravitational field does not necessarily constitute giving the nature of reality for the gravitational force. The theory gives a coordinate
acceleration of
, determining the motion of a material point in a
gravitational field does not necessarily constitute giving the nature of reality for the gravitational force. The theory gives a coordinate
acceleration of 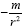 , which is the coordinate acceleration of a material point in a gravitational field, but Einstein’s space-time
coordinates, as determined by the Schwarzschild solution, give an approximate coordinate acceleration of
, which is the coordinate acceleration of a material point in a gravitational field, but Einstein’s space-time
coordinates, as determined by the Schwarzschild solution, give an approximate coordinate acceleration of 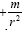 if and only if the
material point moves with a constant velocity
if and only if the
material point moves with a constant velocity 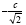 in flat space–time along the geodetic line. If the falsity of this last circumstance
were obvious or not, we need to show that this condition just does not happen [19]. The culprit, assuming that the material point
moves in a geodetic line in the first place, here is that Einstein does not chose the space-time coordinates so that
in flat space–time along the geodetic line. If the falsity of this last circumstance
were obvious or not, we need to show that this condition just does not happen [19]. The culprit, assuming that the material point
moves in a geodetic line in the first place, here is that Einstein does not chose the space-time coordinates so that
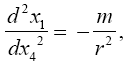 (5.5)
(5.5)
but, rather, so that
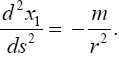 (5.6)
(5.6)
If the irony of this state of affairs is not apparent, we note that the measurement of the acceleration of a material point in the gravitational field gives the value
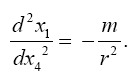 (5.7)
(5.7)
By assuming, as readily suggested by itself, that a material point moves in a geodetic line and taking the space-time coordinates to be such that
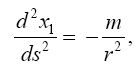 (5.8)
(5.8)
Einstein guarantees that his space-time coordinates correspond to a faster clock and a larger unit of distance and that the measured velocity and acceleration of a material point in a gravitational field are what we just gave. According to the general theory of relativity, the measured acceleration of a material point in a gravitational field is given by
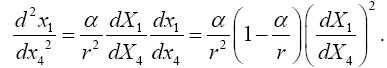 (5.9)
(5.9)
This does not give Newton’s law of gravitation as an approximation.
"Thus, trivially, the Schwarzschild solution, once again, described by Wald as “the general solution, first discovered by Schwarzschild, of the vacuum Einstein equation corresponding to static, spherically symmetric space times” and considered by Einstein as the solution of the equation of the geodetic line such that"
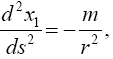 (5.10)
(5.10)
has no chance of being that which Wald, or anyone else, claims. Trivially, by inspection, we showed in Part 1 that the given time coordinate corresponds to a faster clock and not a slower clock as claimed by Einstein and everyone else.
Any claim that the theory has been experimentally verified is, of course, nonsense since no theory can be verified by what it implies being true. In the case of relativity, experiments, as shown in Part 3, which measure the difference of the rate of clocks in a gravitational field, confirm a slower clock and not the faster clock that relativity implies. Thus, at the most fundamental level, experimental evidence contradicts the theory.
Claims of proof based on the notion that hundreds of thousands of mathematicians have verified the theory, as one astrophysicist from the NRAO recently claimed, or the idea that all of the great minds have confirmed the theory, which was not initially accepted, do not make the theory true. Such claims of proof do not consider the theory at all, but rely on presupposing that a completely hypothetical consideration of theory by genii and sub genii, who, according to the hypothesis, find it to be true, makes the theory true.
In order to consider, with the space-time coordinates such that each diagonal g'μυ is the multiplicative inverse of the gμν given
by the Schwarzschild solution and such that the non-diagonal g'μυ vanish, whether a material point moves in a geodetic line along
a path for which the path in space lies along a radius, we assume that this is the case. Once again, if the positive X1 axis is aligned
along a radius, X1 increasing with increasing r, and the x1 and x4 axes in the gravitational field are aligned with the corresponding
axes in flat space-time, we have, for the velocity 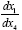 of the material point in the gravitational field,
of the material point in the gravitational field,
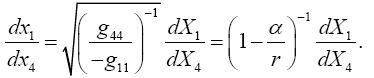 (5.11)
(5.11)
With these coordinates, for the acceleration, 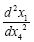 which must equal the measured acceleration in the gravitational field, we
have, once again, by the chain rule,
which must equal the measured acceleration in the gravitational field, we
have, once again, by the chain rule,
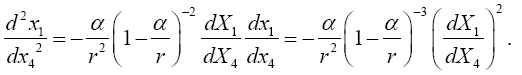 (5.12)
(5.12)
Thus, even though the acceleration 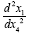 has the correct sign with these coordinates, in order for the first order approximation
to be
has the correct sign with these coordinates, in order for the first order approximation
to be 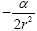 , which is the value of the measured acceleration due to gravity, just as for the Schwarzschild coordinates, we must have
, which is the value of the measured acceleration due to gravity, just as for the Schwarzschild coordinates, we must have
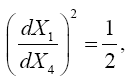 (5.13)
(5.13)
or
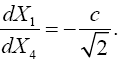 (5.14)
(5.14)
The problem with the velocity of the material point being 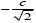 in flat space-time is that either
in flat space-time is that either
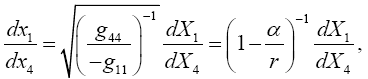 (5.15)
(5.15)
or, in the Schwarzschild case,
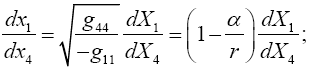 (5.16)
(5.16)
thus, in either case, by continuity, given ε > 0, for sufficiently large r, the velocity of the material point in the gravitational field must be within ε of its velocity in flat-space time. According to Newtonian theory, for sufficiently large r, the velocity of the material point is arbitrarily close to zero.
More generally, for a material point with velocity 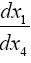 given by
given by
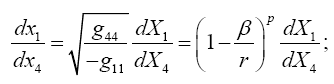 (5.17)
(5.17)
the acceleration 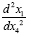 is given by
is given by
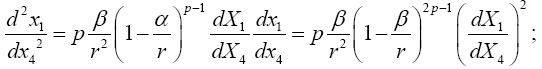 (5.18)
(5.18)
hence, we must have
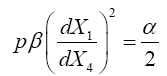 (5.19)
(5.19)
for the absolute value of the acceleration to have a first order approximation of  ; hence, if we contrive to obtain spacetime
coordinates, by taking p to be negative and large, for which the motion of the material point is a geodetic line with first order
approximate acceleration
; hence, if we contrive to obtain spacetime
coordinates, by taking p to be negative and large, for which the motion of the material point is a geodetic line with first order
approximate acceleration  , we have continuity problems for large r even though we can shrink
, we have continuity problems for large r even though we can shrink 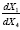 . For sufficiently small r, with
. For sufficiently small r, with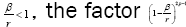 , in the expression for the acceleration, becomes arbitrarily large. The corresponding factor,
, in the expression for the acceleration, becomes arbitrarily large. The corresponding factor,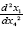 , in the
expression for the acceleration
, in the
expression for the acceleration 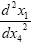 using the Schwarzschild coordinates becomes arbitrarily small as
using the Schwarzschild coordinates becomes arbitrarily small as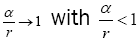
In the case of the inverted Schwarzschild coordinates, the demonstrated failure of a material point to move in a geodetic line, with the path in space along a radius, with these coordinates does not imply that these are not the correct coordinates. In the case of the Schwarzschild coordinates, the experimentally verified slower clock rate in a gravitational field implies that these are not the correct coordinates.
Although no statement or theory can be proved as a result of what it implies being true, Einstein uses exactly this reasoning, that p implies q true and q true imply that p is true, to claim proof of relativity and all of his assumptions even though what the theory implies is actually contradicted at the most fundamental level by the evidence as we showed with Einstein’s space-time coordinates in Part 1. As we showed in Part 2, the Chou, Wineland experiment, which claims to verify Einstein’s relativistic clock rate for clocks in a gravitational field, verifies instead the clock rate, which is based on equivalence principle arguments and given in Einstein’s 1911 paper, On the Influence of Gravitation on the Propagation of Light, and which is not equivalent to the relativistic clock rate.
In Part 5 we showed that by assuming that a material point moves in a geodetic line and that the coordinate acceleration 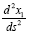 along a radial path in space is given by
along a radial path in space is given by
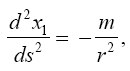 (6.1)
(6.1)
instead of assuming that
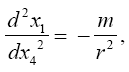 (6.2)
(6.2)
“Einstein guarantees that his space-time coordinates correspond to a faster clock and a larger unit of distance and that the measured velocity and acceleration of a material point in a gravitational field are what we just gave.”
Einstein’s assumption, which readily suggested itself, that a material point moves in a geodetic line is the basis of relativity theory and is one of the assumptions that gets “verified” as a result of the “truth” of the implications of the theory.
In Influence, Einstein argues, via the Doppler principle, that in a uniformly accelerated system K′, light emitted at S2 with frequency ν2 has frequency ν1 with respect to an identical clock at S1 upon its arrival at S1, the frequency given to a first approximation by
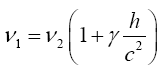 (6.3)
(6.3)
By the principle of equivalence, this same equation holds to a first approximation in a system of coordinates K at rest in a homogeneous gravitational field. For γ h, Einstein substitutes the gravitational potential Φ of S2, with the gravitational potential of S1 taken as zero, obtaining (Figure 7):
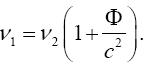 (6.4)
(6.4)
In Part 2, we showed the equivalence of the equation that Chou, Wineland verify with Einstein’s eqn. (2) in Figure 6,
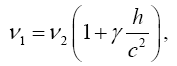 (6.5)
(6.5)
from Influence so that
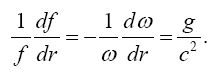 (6.6)
(6.6)
For γ, g in these last two equations
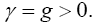 (6.7)
(6.7)
In Part 2 we considered the clock rate f' if g44 is the multiplicative inverse, i.e.,
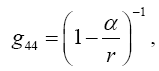 (6.8)
(6.8)
of Einstein’s value. By our previous result in Part 2, we have
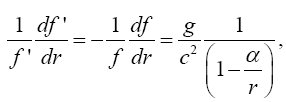 (6.9)
(6.9)
where f is Einstein’s clock rate in Foundation. Thus, the clock rate f′ is one first-order approximate solution of
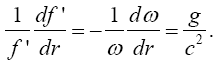 (6.10)
(6.10)
Another such approximate solution is given by, for example,
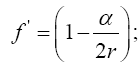 (6.11)
(6.11)
we have
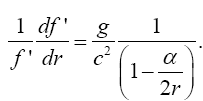 (6.12)
(6.12)
\If the distance coordinate x1, aligned along a radius in the gravitational field, does not vary so that g11 = 1 and the clock rate is that above for
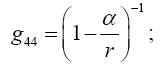 (6.13)
(6.13)
then, if a material point moves in a geodetic line with these coordinates, we have, by the chain rule,
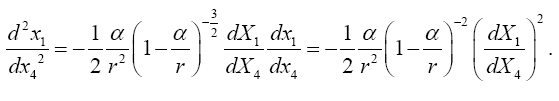 (6.14)
(6.14)
Thus, if a material point moves in a geodetic line with these coordinates, in order for the first order approximation to be 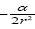 , which is the value of the measured acceleration due to gravity, we must have
, which is the value of the measured acceleration due to gravity, we must have
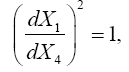 (6.15)
(6.15)
or
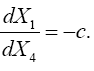 (6.16)
(6.16)
A material point, with a path in space aligned along a radius, does not move in a geodetic line just because Einstein assumed that it moves in a geodetic line and Einstein claimed that the theory implies Newton’s law of gravitation and the precession of the perihelion of the orbit of the planet Mercury. We have shown repeatedly that Einstein’s theory does not imply Newton’s law of gravitation; even if Einstein’s theory implies every result that Einstein states that it implies, the validity of Einstein’s assumptions is not established by the implications of these assumptions being true [20].
Such is the nature of relativity, developed, as Einstein’s “main object,” “in such a way that the reader will feel that the path we have entered upon is psychologically the natural one, and that the underlying assumptions will seem to have the highest possible degree of security,” that we somehow consider, in the face of proof that, with Einstein’s space-time coordinates, the inverted Schwarzschild coordinates, or with the coordinates just given in which only the time coordinate varies, a material point cannot possibly move in a geodetic line, that a material point moves in a geodetic line in the space-time coordinates of a gravitational field.
The experimentally verified, by Chou, Wineland, clock rate, which is the same thing as clock frequency, is any clock rate that satisfies, to a first approximation,
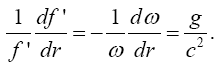 (6.17)
(6.17)
Thus, we have given above two such approximate solutions. The experimental result is that the clock frequency in a gravitational field is given by something like, or approximately,
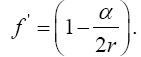
We have yet to reflect on, other than in the consideration of the Schwarzschild coordinates and the inverted Schwarzschild coordinates as solutions of the equation of the geodetic line, the change in the distance coordinate, aligned along a radius, in a gravitational field. If there exists an experimentally verified result, we have yet to consider that either.
Rather than considering Einstein’s premises or results in order to determine the change, if any, in the distance coordinate along a radius, we can argue logically on this matter by considering a simple clock, the hydrogen atom, in the gravitational field. For the lowest energy level, n = 1, the circumference of the atom is the wavelength λB of the de Broglie wave associated with the electron. The frequency νB of this de Broglie wave is the clock frequency. Using the experimental result that, approximately,
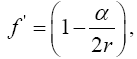 (6.19)
(6.19)
a decrease, corresponding to a the unit of distance getting smaller, in the Bohr radius of the atom by some factor β, forces
the de Broglie wave velocity νB to decrease by both β and 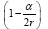
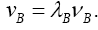 (6.20)
(6.20)
Although there is no known condition, or than by premise, that implies that this decrease in the Bohr radius, and corresponding
change in the de Broglie wave velocity by both β and 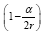 , does not occur, we assume for the purpose of argument that there
is no change in the unit of distance along a radius in a gravitational field.
, does not occur, we assume for the purpose of argument that there
is no change in the unit of distance along a radius in a gravitational field.
In making this last assumption, we note that we seek the nature of reality for the gravitational force; we adhere to the concept that a rational explanation for the gravitational force, and reality in general, exists. Otherwise, the end eavor that we call physics is a waste of time. In a sense, Einstein wasted our time for a hundred years. As far as replacing Einstein’s theory by a better one, we note that we have proved that every result, obtained by assumption or otherwise, of the theory to be false.
Before we shed any tears for Einstein, the physicists, the scientific community and the clowns, we note the words of Bob Dylan as follows:
Come mothers and fathers Throughout the land And don't criticize What you can't understand Your sons and your daughters Are beyond your command Your old road is Rapidly agin' Please get out of the new one If you can't lend your hand For the times they are a-changin'.
We could seemingly go on endlessly with this, adding another part or two, before we explain the nature of the gravitational force; but, in a sense, either we have it or we do not. Simply put, the gravitational force is a mechanism for converting the energy of the de Broglie wave clocks contained in a material point into the kinetic energy of the material point.
In The Feynman Lectures in Physics, Volume 1, Chapter 4, Feynman states,
“There is a fact, or if you wish, a law, governing all natural phenomena that are known to date. There is no known exception to this law—it is exact so far as we know. The law is called the conservation of energy. It states that there is a certain quantity, which we call energy that does not change in the manifold changes which nature under goes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same. (Something like the bishop on the red square, and after a number of moves—details unknown—it is still on some red square. It is a law of this nature.) Since it is an abstract idea, we shall illustrate the meaning of it by analogy.”
Now, Feynman and the rest of the scientific community, who have no idea where the energy that a material point gains, in moving from ∞ to a radius r, comes from, invent a source and call it the gravitational potential energy so that the law of conservation of energy holds. According to the Newtonian theory of gravitation, with the gravitational force on a material point of mass equal to
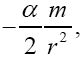 (6.21)
(6.21)
we have for where the energy that a material point gains, in moving from ∞ to a radius r,
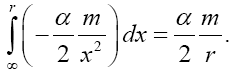 (6.22)
(6.22)
The gravitational potential energy, the additive inverse of the energy that the material point gains, at r is thus
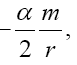 (6.23)
(6.23)
so that the total energy, which is conserved, is equal to zero.
Now, if the energy of the electron de Broglie wave is given by
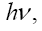 (6.24)
(6.24)
the change in the energy of the electron de Broglie wave if the hydrogen atom moves from ∞ to a radius r is given by, assuming the experimentally verified approximate clock rate,
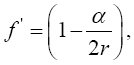 (6.25)
(6.25)
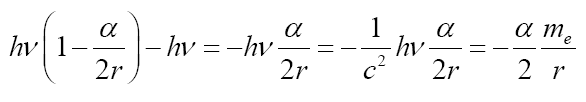 (6.26)
(6.26)
since the unit of time is chosen so that c = 1.
The assumption that the velocity, for infinite r, of the electron de Broglie wave is just C has not been made. In consideration of the hydrogen atom as a miniature Michelson-Morley experiment in The Material Point Universe Revisited, we concluded that the electron de Broglie wave velocity must be C in order that hydrogen atom moving at a velocity ν be a Michelson-Morley experiment.
In the Michelson-Morley experiment, light, which should move in the perpendicular direction with a velocity C if the apparatus were at rest, moves instead along the hypotenuse of a right-triangle with a velocity C if the apparatus moves in the parallel direction with a velocity ν since light moves with a velocity C along whatever path it takes [21].
Similarly, in the hydrogen atom, as long as the velocity c′ of the de Broglie wave is maximal, the electron de Broglie wave moves with a velocity c′ along a semi-circular path in the perpendicular direction if the atom is at rest and with a velocity c′ along an extended semi-circular path if the atom moves in the parallel direction with a velocity ν.
There exists exactly one right-triangle with perpendicular length B, parallel length νt, and hypotenuse of length c′ t. For the
t that it takes the de Broglie wave to move along its extended semi-circular path, the length of the projection of this path on the
perpendicular is λB. As long as the path, when the atom is at rest, of the de Broglie wave is in the perpendicular direction, the point
wise projected velocity of the de Broglie wave on the perpendicular is 
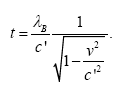 (6.27)
(6.27)
This value for t is half of the period, which corresponds to the unit of time, of the de Broglie wave clock in the perpendicular direction. Thus, in order for this clock to slow down by a factor of 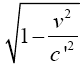 , we must have
, we must have
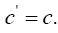 (6.28)
(6.28)
Hence, for infinite r, the velocity of the electron de Broglie wave in the hydrogen atom is c.We have shown that the energy that an electron, in a hydrogen atom, gains, according to Newtonian theory, in moving from ∞ to a radius r, is equal to the energy that the electron de Broglie wave loses if the hydrogen atom moves from ∞ to a radius r. While this does not prove that the source of the increase in the energy of motion of the electron is the energy that the electron de Broglie wave loses, there are no other known possibilities. By the law, which Feynman calls a fact, of conservation of energy, the energy that the de Broglie wave loses must go somewhere and the energy that the electron gains must have a source; thus, there is no known alternative to what we suspect is the case.
Although the laws of physics may be no more factual than Einstein’s postulates, which are nothing more than premises that we have universally found to be false, we consider the law of conservation of energy to be, at the very least, consistent with, if not necessary for, a rational explanation of reality.
Assuming, once again, that there is no change in the distance coordinates along a radius in a gravitational field, we consider, as a rational explanation of reality for the gravitational force on a hydrogen atom, the hydrogen atom to consist of nested de Broglie wave clocks that account for the entire mass/energy of the atom. The same equations that we have given for the changes in the energies of the electron and the electron de Broglie waves apply to each de Broglie wave clock and the particle associated with it.
For a hydrogen atom, initially at rest at infinity in a gravitational field, the atom moves, along a radius, with increasing energy
of motion at the expense of the de Broglie wave clocks until the energy of the de Broglie wave clocks is exhausted at a radius 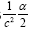 , at which point the hydrogen atom collapses, becoming part of what, with different attributes, has previously been called a black
hole. If the clock rate along a radius is the inverted Schwarzschild clock rate, i.e.,
, at which point the hydrogen atom collapses, becoming part of what, with different attributes, has previously been called a black
hole. If the clock rate along a radius is the inverted Schwarzschild clock rate, i.e.,
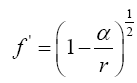 (6.29)
(6.29)
then the energy of the de Broglie wave clocks is exhausted at a radius 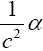 We have shown that for
We have shown that for
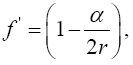 (6.30)
(6.30)
“the energy that an electron, in a hydrogen atom, gains, according to Newtonian theory, in moving from ∞ to a radius r, is equal to the energy that the electron de Broglie wave loses if the hydrogen atom moves from ∞ to a radius r.” Since this clock rate gives exactly the Newtonian value for this change in energy and since, as a result of the theory of relativity, without even considering the effect of velocity on mass, we expect a variance from Newtonian results, we suspect that this experimentally verified approximate clock rate is, in fact, just an approximation of the actual clock rate [22].
Even if the phenomenon of gravitation is independent of the effect of velocity on mass, then, oddly, the effect of velocity on clock rate foretells the effect of gravitation on clock rate. We cannot automatically assume the exact opposite of whatever the scientific community considers to be the correct theory of a given phenomenon; rather, we must separately consider each observable fact/theory. If we conclude that something other than a given theory is true, then the conclusion is based on logical arguments.
If the expression 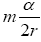 , which gives the Newtonian value for the energy that a material point gains in moving from infinity to a radius r, is equal to
, which gives the Newtonian value for the energy that a material point gains in moving from infinity to a radius r, is equal to 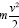 , the classical value for the kinetic energy of the material point after moving in this way, then
, the classical value for the kinetic energy of the material point after moving in this way, then
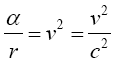 (6.31)
(6.31)
since the unit of time is chosen so that the velocity of light is equal to one. Thus we have
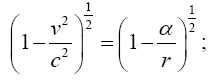 (6.32)
(6.32)
thus, assuming the inverted Schwarzschild clock rate in the gravitational field of
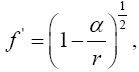 (6.33)
(6.33)
the clock rate of the de Broglie wave clock of a hydrogen atom moving from infinity to a radius r, ignoring any variance due to
the gravitational field, changes by a factor 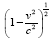 that is equal to the factor
that is equal to the factor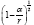 that gives the clock rate of the de Broglie wave
clock of a hydrogen atom at rest at a radius r in the gravitational field in comparison to the clock rate of the de Broglie wave
clock of a hydrogen atom at rest at infinity. This is not an equivalence principle from which we argue; for the given clock rate, it is
a conclusion.
that gives the clock rate of the de Broglie wave
clock of a hydrogen atom at rest at a radius r in the gravitational field in comparison to the clock rate of the de Broglie wave
clock of a hydrogen atom at rest at infinity. This is not an equivalence principle from which we argue; for the given clock rate, it is
a conclusion.
To depart from Einstein’s relativity theories, with claims of their experimental verification, logical completeness, and ultimate truth, even to the point of explaining everything there is to explain, leaves one with the seemingly endless questions that the theories never explained at all. We have repeatedly shown that all of the claims just mentioned are nonsense; yet any opposing theory is perceived as lacking these qualities. These works have been rejected without any consideration, from Richard Sonnenfeld of New Mexico Tech stating that there had to be an error because the theory had been proved and that he could find the error in fifteen minutes, but he just did not have the time, to James Binney, director of the Peierls Center for theoretical physics at Oxford University, stating, evidently unaware that contradictions imply the falsity of an assumption, that “if you step outside of Einstein's framework in setting up the problem, it is to be expected that you arrive at a contradiction.” When one shows that they are wrong, they, and all of the rest of the cowed and ignorant scientific community, just ignore it.
We give a few of the open questions:
whether the velocity of light changes as it approaches a mass,
whether the distance coordinate changes in the gravitational field,
and whether black holes attract each other.
The consideration, in a gravitational field, of whether the velocity of light changes, whether the distance coordinate changes, and whether light clocks move more slowly parallels the reflection just given for the de Broglie wave clocks of a hydrogen atom. In the case of the electron de Broglie wave clock in the hydrogen atom, a change in the distance coordinate implies the same change in the length of the de Broglie wave. An increase in the Bohr radius and constant de Broglie wave velocity gives a slower clock by the same factor by which the Bohr radius increases [23]. The assumption of a constant Bohr radius requires that we obtain a slower clock by decreasing the de Broglie wave velocity/frequency. We did not consider the change in electron de Broglie wave frequency in a gravitational field in any other circumstances.
In the case of a light clock in a gravitational field, we, apparently, do not have light circling the nucleus of a hydrogen atom. We might consider a light clock consisting of light moving along a radius, being reflected by a mirror, and returning to its original position, the time for this to occur corresponding to the period or unit of time for the clock. If the length, as measured by measuring rods in flat space-time, that the light travels is longer than the length it should have in flat space-time by a factor of β and the velocity of the light in flat space-time, that is, as measured by measuring rods and clocks of flat space-time, is c, then the unit of time for the clock increases by a factor of β and the clock runs more slowly by a factor of β.
If the rate of the electron de Broglie wave clock of the hydrogen atom along a radius is the inverted Schwarzschild clock rate, i.e.,
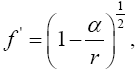 (6.34)
(6.34)
and
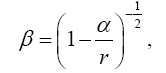 (6.35)
(6.35)
which is the Schwarzschild value, then the period of the light clock changes by the factorβ, the same factor by which the unit of the electron de Broglie wave clock of the hydrogen atom changes and the frequency, as measured by the electron de Broglie wave clock of the hydrogen atom, of the light is equal, to a first approximation, to the value required by the equivalence principle. We seemingly ignore, here, that in the consideration of the electron de Broglie wave clock of the hydrogen atom, we assumed that there is no change in the distance coordinate along a radius; we did not consider a change in the distance coordinate along a radius such that the unit of distance increases for the reason given one paragraph hence. The argument here is that with respect to any clock, e.g., by assumption, the electron de Broglie wave clock of the hydrogen atom, with an inverted Schwarzschild clock rate, the period of the given light clock, with increased length β and constant velocity of light with respect to flat space-time, changes by the factor β, the same factor by which the unit of the electron de Broglie wave clock of the hydrogen atom changes and the frequency of the light is equal, to a first approximation, to the value required by the equivalence principle. In a sense, we can compare, just as we have done, the properties of these two clocks; unfortunately, the given light clock does not exist if the distance coordinate does not change, which is what we assumed in the case of the electron de Broglie wave clock of the hydrogen atom, along a radius. If we assume, contrary to the perception, one paragraph hence, that the unit of distance decreases along a radius, that the Bohr radius of the hydrogen atom increases by a factor β, with
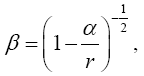 (6.36)
(6.36)
then the electron de Broglie wavelength must also increase by the factor β; thus, for the rate of the electron de Broglie wave clock of the hydrogen atom along a radius to be the inverted Schwarzschild clock rate, the frequency of the electron de Broglie wave must decrease by a factor
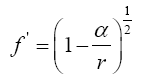
since the de Broglie wave frequency is the clock frequency. In this case, the velocity of the de Broglie wave does not change at all, and the frequency of the light, with constant velocity with respect to flat space-time, in the light clock, the length of which increases by
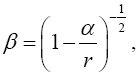 (6.38)
(6.38)
increases by a factor of 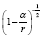 as measured by the electron de Broglie wave clock of the hydrogen atom, thus satisfying the
requirement of the equivalence principle.
as measured by the electron de Broglie wave clock of the hydrogen atom, thus satisfying the
requirement of the equivalence principle.
Just as the Schwarzschild clock rate, which gives the rate of a faster clock, is taken to be rate of a slower clock, the Schwarzschild distance coordinate, which corresponds to a larger unit of distance, is taken to give a smaller unit of distance. Thus the “result,” experimentally verified or not and given by the Schwarzschild distance coordinate or not, is that lengths get smaller. In The Material Point Universe, we stated [24],
‘In General Relativity, Wald notes that sufficiently massive bodies will undergo complete gravitational collapse; moreover, Wald states, “…at all stages of the collapse the metric outside the body will be the Schwarzschild metric, since, as mentioned at the end of section 6.1, it is the only spherically symmetric vacuum solution of Einstein’s equation” and “the complete collapse of a spherical body always produces a Schwarzschild black hole region of space time.”’
If the length, aligned along a radius in a gravitational field, of the light clock is shorter than the length it should have in flat space-time by a factor of β, then, in order that the light clock slow down, with respect to a clock in flat space-time, by a factor of
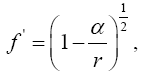 (6.39)
(6.39)
which is inverted Schwarzschild clock rate, the velocity of the light in flat space-time, that is, as measured by measuring rods and clocks of flat space-time, must decrease by both multiplicative factors β and f'.
If we assume that the Bohr radius of the hydrogen atom decreases by a factor β, with
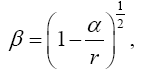 (6.40)
(6.40)
then the electron de Broglie wavelength must also decrease by the factor β; thus, for the rate of the electron de Broglie wave clock of the hydrogen atom along a radius to be the inverted Schwarzschild clock rate, the frequency of the electron de Broglie wave must decrease by a factor
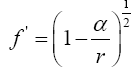 (6.41)
(6.41)
since the de Broglie wave frequency is the clock frequency. The velocity of the de Broglie wave decreases by the factor
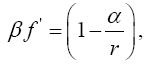 (6.42)
(6.42)
which is the same factor by which the velocity of light in the light clock changes; in the light clock, on the other hand, since the wavelength of the light does not change, the frequency of the light must change by this factor. Thus, with respect to both the electron de Broglie wave clock of the hydrogen atom and the light clock, the frequency of the light in the light clock must decrease by the factor
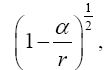 (6.43)
(6.43)
in disagreement with the requirement of the equivalence principle that it increase by the factor
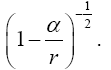 (6.44)
(6.44)
Assuming a constant wavelength, for the frequency, as measured by the electron de Broglie wave clock of the hydrogen atom, of the light in the light clock to agree with the equivalence principle, the frequency and, hence, the velocity, as measured in flat space-time, of the light in the light clock cannot change. This implies, in the case that the length, aligned along a radius in a gravitational field, of the light clock is shorter than the length it should have in flat space-time by a factor of β, that rate of the light clock increases by the factor
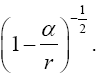 (6.45)
(6.45)
More generally, if the de Broglie wave clock of the hydrogen atom slows down by the factor
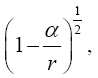 (6.46)
(6.46)
then, assuming a constant wavelength, the frequency and, hence, velocity of light moving along a radius cannot change, with respect to flat space-time, in order that its frequency, as measured by the de Broglie wave clock of the hydrogen atom, agree with the equivalence principle.
The conclusion, that the change in frequency of light according to the equivalence principle by the appropriate factor is a result of clocks moving more slowly by the inverse of this factor, was made by Einstein in his 1911 paper, On the Influence of Gravitation on the Propagation of Light.
Assuming for now, without any other consideration, the constancy of the velocity and the wavelength of light with respect to flat space-time, the value for the frequency of light given by the equivalence principle has been experimentally verified; hence, we may replace the phrase in agreement with the equivalence principle in the above statements with in agreement with experiment.
Now, the open question, whether the velocity of light changes as it approaches a mass has seemingly been answered, but, for one, the preceding argument assumed a constant wavelength; hence, without giving any other arguments, we must proceed with caution.
These considerations, which are hardly necessary in Einstein’s general relativity, particularly since that theory cannot withstand them, are seemingly endless. When we mentioned to Huib Intema of the NRAO that clocks slow down along a radius with respect to flat space-time by a factor of
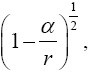 (6.47)
(6.47)
he, ignoring that we stated along a radius with respect to flat space-time, stated, paraphrased somewhat, that it depended on to what we were making the comparison, that, for example, with respect to itself, such a clock did not change at all. Intema and Rick Aster, the arrogant former professor of geophysics at New Mexico Tech, had ignored Bender in their discussions of their incredible work, prompting Bender to attempt a discussion of relativity. On that topic, Aster spoke, at the limits of his understanding, of gravitational wells and of the necessity of solving the wave equation in the case of the Bohr radius of the hydrogen atom, and Intema continued to insist that, with respect to themselves, clocks do not change at all. Thus Intema and Aster succeeded in deflecting Bender’s attempts to enlighten them.
That this work must end shortly, five or ten pages more at most, is a consequence of the endlessness of these arguments and the intent that this paper be finite. If complete enlightenment has not been achieved, we must pass on it here, waiting for another day. Where we once felt inadequate to consider the nature of reality for the gravitational force, we believe that we have given it. We have considered, although not in this work, whether black holes attract each other; when we asked Intema if he knew of any evidence that black holes attract each other, he, oblivious to the question of evidence, replied unhesitatingly that they do. We have argued previously that Einstein’s general relativity cannot possibly explain this attraction, if it exists, since the space-time environment of a singular that is, characterized by a singularity, material point is not what Einstein says that it is [25].
We seemingly eliminated the consideration of an increasing unit of distance, corresponding to an increasing Bohr radius of the hydrogen atom, along a radius in the gravitational field, on the perceptual ground that masses collapse to form black holes rather becoming infinitely large. If we have not eliminated the perceived shrinking Bohr radius of the hydrogen atom and corresponding decreasing unit of distance along a radius, we return, nevertheless, to the space coordinate in the middle, that is, in which the unit of distance remains constant along a radius.
When we stated, “Although there is no known condition, or than by premise, that implies that this decrease in the Bohr radius,
and corresponding change in the de Broglie wave velocity by both β and 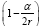 does not occur, we assume for the purpose
of argument that there is no change in the unit of distance along a radius in a gravitational field,” by known condition we included
experimental evidence as perceived by us.
does not occur, we assume for the purpose
of argument that there is no change in the unit of distance along a radius in a gravitational field,” by known condition we included
experimental evidence as perceived by us.
Einstein perceived the experimental evidence to imply general relativity, including his space-time coordinates, via the reverse assertion that general relativity, including his space-time coordinates, which the theory implies, implies the experimental evidence, which includes such diverse matters as Newton’s law of gravitation, the precession of the perihelion of the orbit of the planet Mercury, bending of light, and clock rates in the gravitational field. Einstein’s clock rate dx4, which Einstein refers to, as indicated on the first page of this paper, as the clock rate in the gravitational field, is greater than 1, the clock rate in flat space-time.
Thus the clock rate that the theory implies is not the experimentally verified clock rate; hence, the theory does not imply the evidence. The assertion that the theory implies the evidence was used, by Einstein, to “prove” the theory, which in turn proves the space –time coordinates implied by the theory. The following statements are false (Figure 1):
If the theory implies the evidence, then the theory is true.
The theory implies the evidence.
The theory is true.
Showing that the evidence implies a theory, the only conceivable way to prove the theory, is called a proof. If the argument is sound, that is, valid and all of the premises are true, then the theory is true. In what follows, we consider the experimental evidence that, approximately at least, clocks move more slowly in the gravitational field by the factor
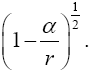 (6.48)
(6.48)
We consider the electron de Broglie wave clock in the lowest energy state in the hydrogen atom to be such a clock and the nucleus of the atom to consist of nested de Broglie wave clocks with the same property. We assume that there is no change in the distance coordinate along a radius; this implies that the wave frequency is the clock frequency. We assume that the velocity of these de Broglie waves in flat space-time is c.
In the case of the distance coordinate, we gave, in the preceding pages, arguments concerning various choices for changes in the distance coordinate; in a sense, no change in the distance coordinate is the simplest case, not that simplicity follows from any postulate known beforehand. As a result of what, in the case of special relativity, Einstein refers to as operation (a) —
“(a) The observer moves together with the given measuring-rod, and measures the length of the rod directly by superposing the measuring-rod, in just the same way as if all three were at rest.”
— we conclude, applying this to the present consideration, that it is not possible to directly verify, by experiment, any change in the distance coordinate in a gravitational field. Any argument, e.g., the one, given by Paul Marmet, claiming that the Pound- Rebka experiment implies that the Bohr radius of the hydrogen atom increases as r, the distance from a given mass, decreases, that experimental evidence gives a change in the distance coordinate is thus open to scrutiny.
The nested de Broglie wave clocks in the hydrogen atom move more slowly and, thus, lose energy by the factor
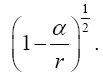 (6.49)
(6.49)
Thus the energy of the hydrogen atom in the gravitational field is given by
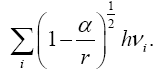 (6.50)
(6.50)
The mechanism for slowing these de Broglie wave clocks is not known, redundantly, the manner by which the de Broglie waves are slowed constituting another open question. This change in clock frequency is driven by the difference in clock rates along a radius passing through the atom; the outer clock rate slows, by decreasing the radius, in an endless attempt to equalize the wave frequency.
The energy that the de Broglie wave clocks lose becomes the energy of motion of the hydrogen atom so that energy is conserved. We have
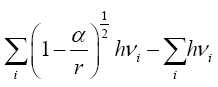
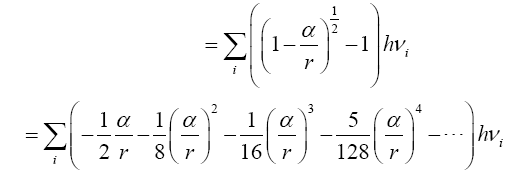 (6.51)
(6.51)
since
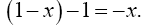
After multiplication by hνi, the first term of the last sum becomes
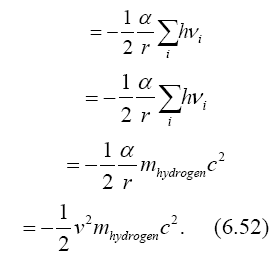
This last expression, obtained by replacing 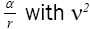 , its classical value, is the classical value for the kinetic energy times
c2. Now previously, when we replaced 1 by c2, we ignored the change in units in the resulting expression. This disregard was only
momentary, reflecting the awkwardness of expressing both the result, which only seemed more important than the change in
units, and the change in units.
, its classical value, is the classical value for the kinetic energy times
c2. Now previously, when we replaced 1 by c2, we ignored the change in units in the resulting expression. This disregard was only
momentary, reflecting the awkwardness of expressing both the result, which only seemed more important than the change in
units, and the change in units.
Now, for example, in part 2, we calculated, for Einstein’s clock rate f, 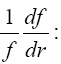
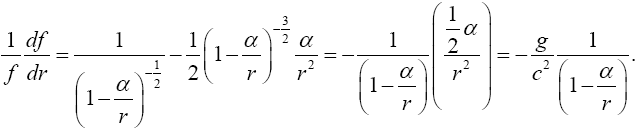 (6.53)
(6.53)
Now 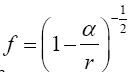 , giving Einstein’s clock rate in the gravitational field as a product of this factor and the clock rate, which is
, giving Einstein’s clock rate in the gravitational field as a product of this factor and the clock rate, which is 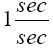 in flat space-time, is, for lack of a better term, quasi-unit less, having units
in flat space-time, is, for lack of a better term, quasi-unit less, having units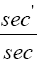 . The expression
. The expression 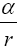 is not unitless, but
is not unitless, but 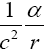 , having the same numerical value, has no units. Thus Einstein’s clock rate, as a quasi-unitless multiplicative factor of
the clock rate in the gravitational field, is given by
, having the same numerical value, has no units. Thus Einstein’s clock rate, as a quasi-unitless multiplicative factor of
the clock rate in the gravitational field, is given by
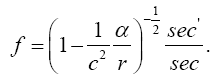 (6.54)
(6.54)
Thus, for the de Broglie wave clocks with the approximate experimentally verified clock rate, which we may now express as
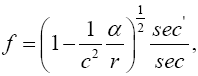 (6.55)
(6.55)
the energy, which the de Broglie wave clocks lose and which the hydrogen atom gains as energy of motion, is given by
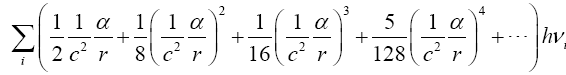
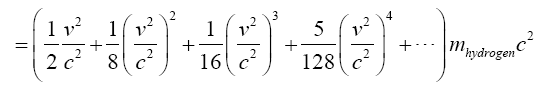
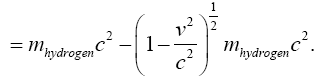 (6.56)
(6.56)
The expression,
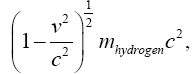 (6.57)
(6.57)
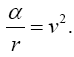 (6.58)
(6.58)
At the radius
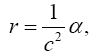 (6.59)
(6.59)
the energy of the de Broglie wave clocks of the hydrogen atom is exhausted; the atom collapses, becoming part of the pea, at the surface of which there are no clocks. By calling this quasi material point a pea, we only give it one of a thousand names. Inside the pea, clocks, apparently, although we can argue the reverse, do not pick them up and count imaginary seconds, moving backward, perhaps, in time. If there are no clocks, in a sense, time, which is what clocks measure, does not exist either. Measuring rods that fall into the pea become part of the pea. The density of the pea is given by
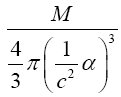 (6.60)
(6.60)
for
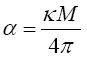 (6.61)
(6.61)
and
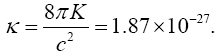 (6.62)
(6.62)
The units here are
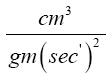 (6.63)
(6.63)
with, for the velocity of light expressed in 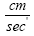 ,
,
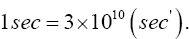 (6.64)
(6.64)
Thus
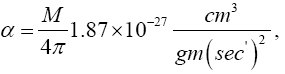 (6.65)
(6.65)
Where M is to be expressed in gm's, and, as a result, (Figure 7):
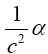 (6.66)
(6.66)
is expressed in cm ’s. Therefore, incredibly, the density of the pea depends inversely on the square of the mass M and is given by
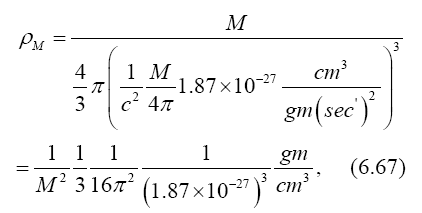
where, in the last expression, M is the mass in gm’s without the units.
The attributes of the pea are debatable; we hedge on its properties. The pea consists of pure homogeneous energy, or, perhaps, matter; or, clocks and measuring rods, and, thus, space-time coordinates, exist. These space-time coordinates satisfy Einstein’s equation; or, perhaps, as is the case outside the pea, the space-time coordinates, which automatically satisfy Einstein’s equation, are not the space-time coordinates for which Einstein solves the equation of the geodetic line.
In Einstein’s 1905 paper, “Does the Inertia of a Body Depend upon Its Energy Content?,” Einstein deduces “a very interesting conclusion” as a result of “the previous investigation.”
Einstein, exhibiting his genius, restates the principle of relativity as:—
The laws by which the states of physical systems alter are independent of the alternative, to which of two systems of coordinates, in uniform motion of parallel translation relatively to each other, these alterations of state are referred [26].
Now at least part of the psychological manipulation or psyching here lies in the assertion that this principle, previously referred to as a postulate, is true. Even in the simplest case, the law, the second postulate, stating that “light is always propagated in empty space with a definite velocity c which is independent of the state of motion of the emitting body,” does not hold, as we proved in The Material Point Universe Revisited, in a system with uniform velocity ν.
The second postulate is, evidently, a law by which the state of the rest system alters or changes; according to the first postulate, it must hold in a system in uniform motion of parallel translation. Thus, both of Einstein’s postulates are false.
In The Feynman Lectures on Physics, Volume I, Feynman, in Section 16-4, states, “We learned in the last chapter that the mass of an object increases with velocity, but no demonstration of this was given, in the sense that we made no arguments analogous to those about the way clocks have to behave.” Paraphrased somewhat, we learned something, which turns out to be false, that Feynman did not demonstrate.
Here, Feynman, “by arguing from the principle of relativity that the laws of physics must be the same in every coordinate system,” demonstrates that the formula for mass, as a function of velocity, mν, is given by
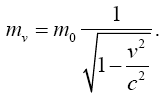 (6.68)
(6.68)
According to Feynman, the principle of relativity was first stated by Newton, in one of his corollaries to the laws of motion: “The motions of bodies included in a given space are the same among themselves, whether that space is at rest or moves uniformly forward in a straight line.” Feynman remarks, “This means, for example, that if a space ship is drifting along at a uniform speed, all experiments performed in the space ship and all the phenomena in the space ship will appear the same as if the ship were not moving, provided, of course, that one does not look outside. That is the meaning of the principle of relativity.” The only question, according to Feynman, is whether this simple idea is true.
Feynman first considers whether Newton’s laws appear the same in the moving system, which moves in the x-direction with uniform velocity u. After the time t, with the two systems coinciding initially, we have
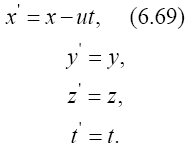
After substitution of this transformation of coordinates into Newton’s laws, Feynman concludes that these laws transform into the same laws in the primed system and that “therefore, it is impossible to tell, by making mechanical experiments, whether the system is moving or not.”
On the other hand, the Maxwell equations of the electromagnetic field, “which describe electricity, magnetism, and light in one uniform system,” did not follow the principle of relativity; that is, after transformation by substitution of the above equations, the form of Maxwell’s equations changes. Feynman notes that “in a moving ship, the electrical and optical phenomena should be different from those in a stationary ship. Thus one could use these optical phenomena to determine the speed of the ship; in particular, one could determine the absolute speed of the ship by making suitable optical or electrical measurements. One of the consequences of Maxwell’s equations is that if there is a disturbance in the field such that light is generated, these electromagnetic waves go out in all directions equally and at the same speed c, or 186,000 mi/sec. Another consequence of the equations is that if the source of the disturbance is moving, the light emitted goes through space at the same speed c. This is analogous to the case of sound, the speed of sound waves being likewise independent of the motion of the source.”
The apparatus in the Michelson-Morley experiment consists of two arms, one parallel to the direction of motion, the other, and perpendicular. These arms are light clocks, the periods of which, if different, give rise to an interference pattern. The experiment does not give the velocity of light or the sum or difference of the velocity of light and the velocity of the ship. Nevertheless, after differentiating the first equation above, resulting in
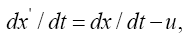 (6.70)
(6.70)
Feynman notes “that according to the Galilean transformation the apparent speed of the passing light, as we measure it in the car, should not be c but should be c-u” Feynman continues, “In any case, by measuring the speed of light going past the car (if the Galilean transformation is correct for light), one could determine the speed of the car. A number of experiments based on this general idea were performed to determine the velocity of the earth, but they all failed—they gave no velocity at all. We shall discuss one of these experiments in detail, to show exactly what was done and what was the matter; something was the matter, of course, something was wrong with the equations of physics. What could it be?”
Now the one experiment that Feynman discusses is, of course, the Michelson-Morley experiment, the result of which Feynman distorts before the discussion. Feynman gives us, in what follows, the “correct” equations of physics.
Attempts to change the Maxwell equations of electrodynamics so “that under Galilean transformation the principle of relativity would be satisfied” took the form of inserting new terms into the Maxwell equations, which “led to predictions of new electrical phenomena that did not exist at all when tested experimentally, so this attempt had to be abandoned. Then it gradually became apparent that Maxwell’s laws of electrodynamics were correct, and the trouble must be sought elsewhere.”
Meanwhile, H. A. Lorentz noticed that Maxwell’s equations remain in the same form after the following substitutions, the Lorentz transformation, are made:
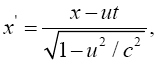 (6.71)
(6.71)
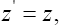
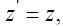
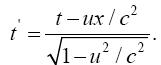 (6.72)
(6.72)
“Einstein, following a suggestion originally made by Poincaré, then proposed that all the physical laws should be of such a kind that they remain unchanged under a Lorentz transformation. In other words, we should change, not the laws of electrodynamics, but the laws of mechanics. How should we change Newton’s laws so that they will remain unchanged by the Lorentz transformation? If this goal is set, we then have to rewrite Newton’s equations in such a way that the conditions we have imposed are satisfied. As it turned out, the only requirement is that the mass min Newton’s equations must be replaced by the form shown in eqn. (6.72). When this change is made, Newton’s laws and the laws of electrodynamics will harmonize.”
Amid this harmony, after Einstein “fixed” the equations of physics with the Lorentz transformation, oddly named after Lorentz, that Feynman, of whom James Gleik, in Genius, stated, “Architect of quantum theories, brash young group leader on the atomic bomb project, inventor of the ubiquitous Feynman diagram, ebullient bongo player and storyteller, Richard Phillips Feynman was the most brilliant, iconoclastic, and influential physicist of modern times. He took the half-made conceptions of waves and particles in the 1940s and shaped them into tools that ordinary physicists could use and understand. He had a lightning ability to see into the heart of problems nature posed. Within the community of physicists, an organized, tradition-bound culture that needs heroes as much as it sometimes mistrusts them, his name took on a special luster. It was permitted in connection with Feynman to use the word genius. He took center stage and remained there for forty years, dominating the science of the postwar era—forty years that turned the study of matter and energy down an unexpectedly dark and spectral road,” argues for, we note that the principle of relativity and the Lorentz transformation are phony.
Rather than place the entire content of The Material Point Universe Revisited and Bender Goes to Oxford, each of which contains dozens of arguments contradicting the principle of relativity, here and exceed the ten page limit, we note that a simple experiment will show that clocks in the moving space ship are not synchronous, thus violating the principle of relativity; moreover, the non-synchronicity of clocks in the moving ship is equivalent to the experimentally verified existence of the Doppler effect. One glance at the last equation, with u negative and x positive, of the Lorentz transformation, that is,
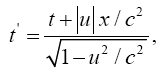 (6.73)
(6.73)
should be sufficient to show that
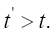 (6.74)
(6.74)
If this gives a slower clock in the moving system, it is at the expense of the coordinate of length parallel to the motion; in Bender Goes to Oxford, we wrote,
“We have
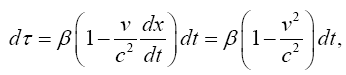 (6.75)
(6.75)
or
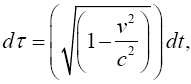 (6.76)
(6.76)
which, at first sight, does give the correct equation for time dilation. When we see this last equation, we are astonished that Einstein did, apparently, come up with the “correct” equations of coordinate transformation [6].
This astonishment lasts until we look at the equation of coordinate transformation for the x-coordinate:
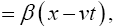 (6.77)
(6.77)
from which, similarly, we obtain
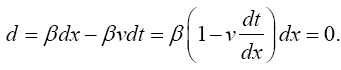 (6.78)
(6.78)
This last equation is, apparently, the correct equation to show that we have destroyed the framework.”
By the Mean Value Theorem, the last equation shows that
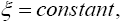 (6.79)
(6.79)
which contradicts the range of ξ.
The silliness of measuring the velocity of light in the moving system, with
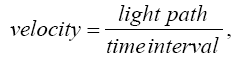 (6.80)
(6.80)
with a smaller unit of distance, the Lorentz contraction, and a larger unit of time, the Lorentz time dilation, and claiming to get c is unbearable. The Lorentz transformation grants us this. The first equation of the Lorentz transformation gives the light path, which, unbelievably, is not even the measured light path in the moving system, which must be the result of operation (a):
“Let there be given a stationary rigid rod; and let its length be l as measured by a measuring-rod which is also stationary. We now imagine the axis of the rod lying along the axis of x of the stationary system of co-ordinates, and that a uniform motion of parallel translation with velocity v along the axis of x in the direction of increasing x is then imparted to the rod. We now inquire as to the length of the moving rod, and imagine its length to be ascertained by the following two operations:—
(a) The observer moves together with the given measuring-rod, and measures the length of the rod directly by superposing the measuring-rod, in just the same way as if all three were at rest.
(b) By means of stationary clocks set up in the stationary system and synchronizing in accordance with § 1, the observer ascertains at what points of the stationary system the two ends of the rod to be measured are located at a definite time. The distance between these points, measured by the measuring-rod already employed, which in this case is at rest, is also a length which may be designated ‘the length of the rod.’
In accordance with the principle of relativity the length to be discovered by the operation (a)—we will call it ‘the length of the rod in the moving system’—must be equal to the length l of the stationary rod.
The length to be discovered by the operation (b) we will call ‘the length of the (moving) rod in the stationary system.’ This we shall determine of the basis of our two principles, and we shall find that it differs from l.”
The remaining consideration here, having by now exceeded the ten page limit, is the bending of light in a gravitational field. As noted in Part 4, Einstein, without any arguments, remarks, “We easily recognize that the course of the light-rays must be bent with regard to the system of co-ordinates, if the gμν are not constant.” In what amounts to assuming, similar to assuming, before now shown to be false, that the acceleration of the material point is equal to the coordinate acceleration, in general that the coordinate- wise functions of the path of the light do whatever the corresponding functions of the coordinates do, Einstein assumes, specifically here, that the curvature of the light-ray is given by
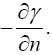 (6.81)
(6.81)
What we have discovered, conversely, is that the space-time coordinates are such that when we measure the acceleration of a material point in a gravitational field with the space-time coordinates that exist there, we obtain for the acceleration
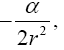 (6.82)
(6.82)
with 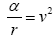 ; and the frequency or clock rate and, hence, energy, of the de Broglie wave clocks of the hydrogen atom decreases
by a factor of
; and the frequency or clock rate and, hence, energy, of the de Broglie wave clocks of the hydrogen atom decreases
by a factor of
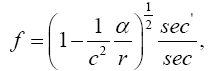 (6.83)
(6.83)
with the distance coordinate along a radius not changing at all, the energy lost by the de Broglie wave clocks going into the energy of motion of the hydrogen atom.
Similarly, perhaps, in the case of a light ray moving perpendicularly to a radius, we have the frequency of the light in the perpendicular direction decreasing by a factor of
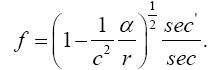 (6.84)
(6.84)
 (6.85)
(6.85)
The energy lost,
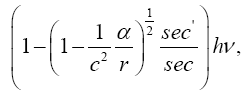 (6.86)
(6.86)
becomes the component in the radial direction of the energy of the resulting light ray.
More generally, for a light ray moving perpendicularly to a radius, if the frequency of the light in the perpendicular direction decreases by a factor of
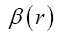 (6.87)
(6.87)
with
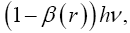 (6.88)
(6.88)
the energy lost, becoming the component in the radial direction of the energy of the resulting light ray. While energy is conserved in the sense that
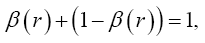 (6.89)
(6.89)
the energy,
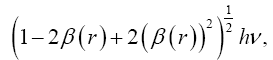 (6.90)
(6.90)
of the resulting light ray is not.
If β(r) is the clock rate at r, then the frequency of the component of light in the radial direction, as measured by the clock at r, is given by
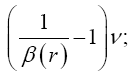 (6.91)
(6.91)
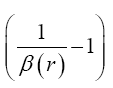 (6.92)
(6.92)
is also, approximately, for sufficiently large r and (r) well-behaved, e.g.,
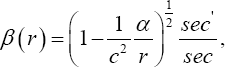 (6.93)
(6.93)
the tangent of the direction of light,
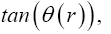 (6.94)
(6.94)
as measured in the distance coordinates of flat space-time. Since there is no change in the distance coordinates in the gravitational field, the same factor gives the tangent of the direction of light in the coordinates of the gravitational field. We imagine a light ray, emitted, perpendicular to a radius, by an atom at infinite r, to correspond to the light ray, emitted by the same atom at finite distance r, at the angle θ (r).
For a light ray, with perpendicular and radial components of energy as above, to have cas its velocity with respect to flat space time, its wavelength must be
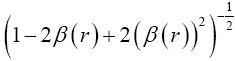 (6.95)
(6.95)
times the value of the wavelength λ corresponding to the frequency . Since for β<1,
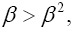
this gives a greater, or red-shifted, wavelength. For
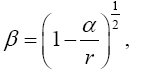 (6.96)
(6.96)
we have, for the wavelength ,
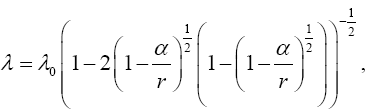 (6.97)
(6.97)
and, for 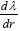 , we have
, we have
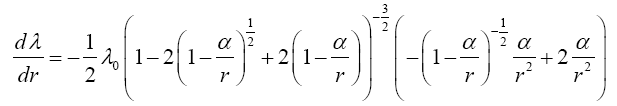
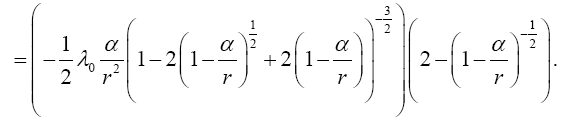 (6.98)
(6.98)
Einstein, with space-time coordinates in the gravitational field given by a clock with rate
 (6.99)
(6.99)
the multiplicative inverse of the actual clock rate, and a distance coordinate, for the x coordinate aligned along a radius, given by, for a unit measure of length in flat space –time,
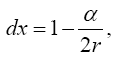 (6.100)
(6.100)
which gives a greater unit of distance rather than the smaller one claimed by Einstein or the actual unit of distance that does not change. Thus equipped, Einstein obtains his value, which we considered in Part 4, for the curvature of a ray of light.
Einstein, without giving an argument, easily recognizes that the course of the light ray must be bent with regard to the system of coordinates if the gν are not constant, the curvature, by the Huyghens principle, of the light ray is given by
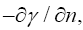 (6.101)
(6.101)
where
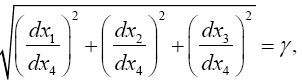 (6.102)
(6.102)
and n is a direction perpendicular to the propagation of light.
For “the curvature undergone by a ray of light passing by a mass M at the distance Δ. If we choose the system of co-ordinates in agreement with the accompanying diagram, the total bending of the ray (calculated positively if concave towards the origin) is given in sufficient approximation by
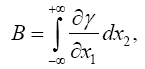
while (73) and (70) give
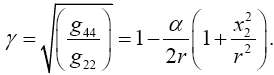
Carrying out the calculation, this gives
Since, by the chain rule for partial derivatives,
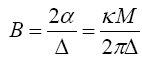
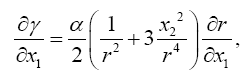 (6.103)
(6.103)
the integral,
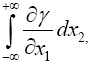 (6.104)
(6.104)
is equal to
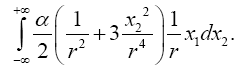 (6.105)
(6.105)
For the integral,
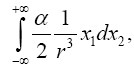 (6.106)
(6.106)
of the first term, we have, for example,
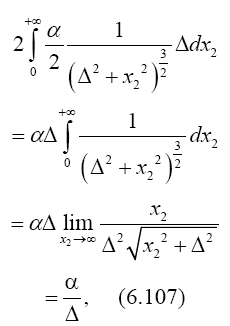
with units that of
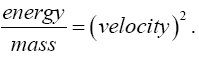 (6.108)
(6.108)
One might argue that Einstein obtains the correct result, the experimental verification of which we have not considered, for the bending of light by considering space-time coordinates with his gμν ’s, inverted in the case of g44, by calculating
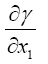 (6.109)
(6.109)
from the wrong direction, that is, in the gravitational field.
We must consider any bending of light around a mass to be observable in flat space-time. On the other hand, since
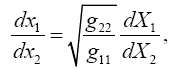 (6.110)
(6.110)
the tangent of the angle that a light ray, perpendicular to a radius, is bent, this bending seemingly contradicting the perpendicularity, is not the same, for non-zero
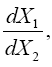 (6.111)
(6.111)
unless
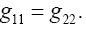 (6.112)
(6.112)
If we multiply
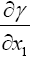 (6.113)
(6.113)
By dx2 to obtain
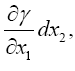 (6.114)
(6.114)
which we may rewrite as
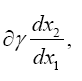 (6.115)
(6.115)
we obtain an expression that contains tan θ, that is,
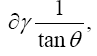 (6.116)
(6.116)
if dx2 is chosen so that
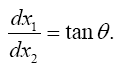 (6.117)
(6.117)
Einstein, although his calculation is in the gravitational field, does not give this value, tan θ. Had he done so, since
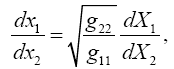 (6.118)
(6.118)
tan θ, if it exists, is either zero, in which case there is no bending, or finite, in which case the value differs from that in flat space-time
Einstein’s measure,
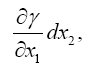 (6.119)
(6.119)
of the bending of light in the gravitational field corresponds to
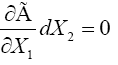 (6.120)
(6.120)
in the coordinates of flat space-time. In Einstein’s expression for the velocity of light,
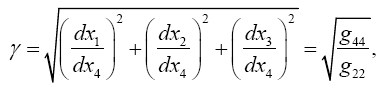 (6.121)
(6.121)
he considers dx1 to be zero, whereas, in the expression for dx4 and the expression for dx2, r varies, which makes γ a function of x1, which varies, so that dx1 cannot be zero, contradicting the assumption that it vanishes.
With Einstein’s inverted gμμ’s, the velocity,
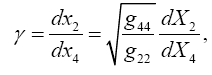 (6.122)
(6.122)
has the same form as
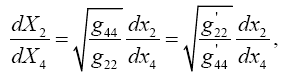 (6.123)
(6.123)
where they gμμ are the actual, non-inverted gμμ. Thus Einstein does not calculate
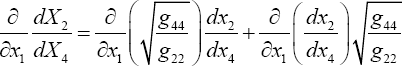 (6.124)
(6.124)
since, by the chain rule for partial derivatives, the partial derivative on the left vanishes. Thus
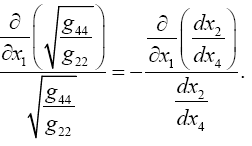 (6.125)
(6.125)
Even if the gμμ are not the multiplicative inverse of the actual g'μμ’s everywhere, or, anywhere, the last equation holds. In fact, for g'μμ are the actual, non-inverted gμμ, we must have
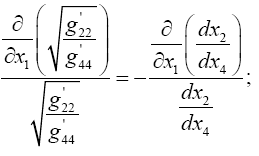 (6.126)
(6.126)
however, as a cautionary note, we have yet to set this up or to consider the aforementioned contradiction.
With respect to the contradiction inherent in concluding that the light path is bent after assuming that it is not bent, we must take this into account in the expression for γ. After assuming the path is straight, Einstein remarks, without proving this that “the total bending of the ray (calculated positively if concave towards the origin) is given in sufficient approximation by
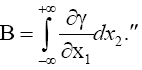
Unfortunately, the path of the light ray cannot be both straight and bent. The condition
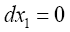 (6.127)
(6.127)
is equivalent to the path of the light ray being straight. If the path is bent, we must have
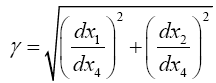 (6.128)
(6.128)
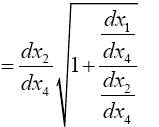
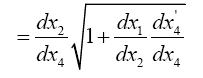
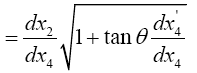
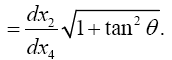 (6.129)
(6.129)
Thus
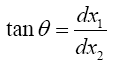 (6.130)
(6.130)
appears naturally in the expression for γ, as measured in the coordinates of the gravitational field. Einstein puts its value at 0 in his expression for γ, the partial derivative, with respect to x1, of which gives Einstein’s value for the curvature of the light ray.
We have, for the real γ,
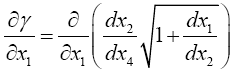
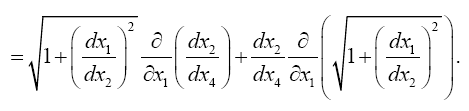 (6.131)
(6.131)
Since
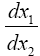
is decreasing,
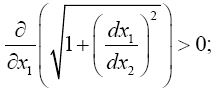 (6.132)
(6.132)
therefore,
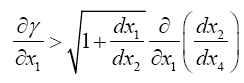
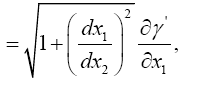 (6.133)
(6.133)
where γ' Einstein’s γ. Thus
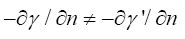 (6.134)
(6.134)
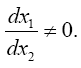 (6.135)
(6.135)
The ambiguity in the value of
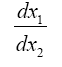
in Einstein’s γ arises from the ambiguity in the path of the light ray. This ambiguity results in a velocity that is not well-defined.
With the space-time coordinates and the value for 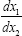 that we have given, we obtain, for a light ray, corresponding to a light ray
perpendicular to a radius in flat space-time, in a gravitational field, for γ the value
that we have given, we obtain, for a light ray, corresponding to a light ray
perpendicular to a radius in flat space-time, in a gravitational field, for γ the value
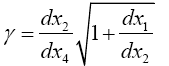
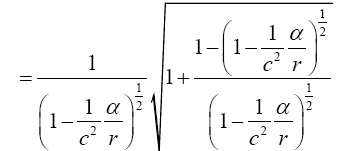
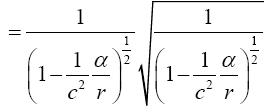
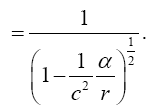 (6.136)
(6.136)
The experimental result for the rate of a clock in a gravitational field is given in the paper, “Optical Clocks and Relativity” by C. W. Chou et al., Science 329, 1630 (2010). The clock rate f satisfies
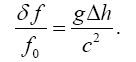 (6.137)
(6.137)
By elementary functional analysis, Einstein’s clock rate,
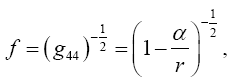 (6.138)
(6.138)
from The Foundation of the General Theory of Relativity is greater than 1, the clock rate in flat space-time, and does not satisfy, as we show in Part 2, the equation that is experimentally verified. On the other hand, the multiplicative inverse of Einstein’s clock rate,
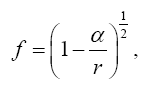 (6.139)
(6.139)
gives a clock rate that is less than 1, thus a slower rate than that in flat space-time, and satisfies the equation that is experimentally verified.
In the lowest energy state of the hydrogen atom, the circumference, the Bohr radius times 2t, of the atom is just the wavelength of the electron de Broglie wave, and the frequency of the de Broglie wave is the frequency of the electron de Broglie wave clock of the hydrogen atom. In the gravitational field at radius r, this de Broglie wave clock has frequency,
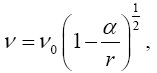 (6.140)
(6.140)
and energy,
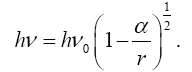 (6.141)
(6.141)
The energy lost,
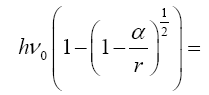
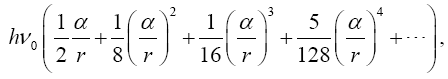 (6.142)
(6.142)
becomes, conserving energy, the energy of motion of the electron de Broglie wave clock and after multiplication by hν0, the first term is the Newtonian value for the gravitational energy of motion of the electron de Broglie wave clock.
Near the beginning of this work, applying beforehand the theory given here directly to astrophysical systems, we stated, “The force holding the astrophysical system known as a star together is gravitation. Deviation of astrophysical bodies from motion in a straight, or geodetic, line is either gravitational or non-existent [6,7]. The astrophysical endeavour of observing astronomical systems to “prove” Einstein’s General Theory of Relativity is, according to the aforementioned works, a waste of time [27].” Adding, to the applications, those given in the body of this work, we argue herein that there is no change in any distance coordinate in a gravitational field, that the gravitational energy of motion of a mass arises from, conserving energy, the energy lost by the nested de Broglie wave clocks of the mass, that the density, incredibly, arbitrarily small for sufficiently large M, of the astrophysical object formerly known as a black hole depends inversely on the square of the mass M, and is given by
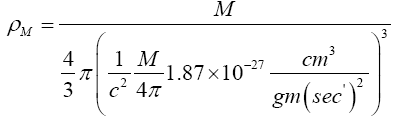
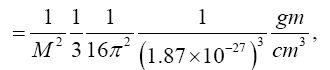 (6.143)
(6.143)
where, in the last expression, M is the mass in gm’s without the units, and that a light ray, emitted, perpendicular to a radius, by an atom at infinite r, corresponds to the light ray, emitted by the same atom at finite distance r, at the angle θ(r), with, for sufficiently large r,
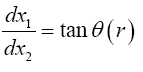
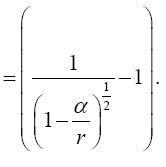 (6.144)
(6.144)
With respect to the correctness of the arguments given herein, we mention here only that Einstein’s clock rate, given in The Foundation of the General Theory of Relativity, in a static gravitational field is that which we have given and that it is trivially greater than 1, the clock rate in flat space-time (Figure 8):
Copyright Disclaimer under Section 107 of the Copyright Act 1976, allowance is made for "fair use" for purposes such as criticism, comment, news reporting, teaching, scholarship, and research. Fair use is a use permitted by copyright statute that might otherwise be infringing. Non-profit, educational or personal use tips the balance in favor of fair use.