ISSN: 2320-2459
ISSN: 2320-2459
IFLP, Fac. de Cs. Exactas, National University La Plata and Buenos Aires Scientific Research Commission (CIC)
Received: 06/13/2015 Accepted: 07/28/2015 Published: 07/30/2015
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Recent work on classical-quantum games is reviewed. We present in game-theory terms the physics associated to the interaction between matter and a single-mode of an electromagnetic field within a cavity, introducing a game admitting of both classical and quantal players. Strategies are determined by the initial conditions of the associated dynamical system, whose time evolution is characterized by the existence of attractors that set the possible results of the game. Two types of quantum states are considered; perfectly distinguishable or partially overlapping ones.
Quantum games, Semi-classical theories
The extension of game theory concepts [1] to the quantum world [2-12] has recently been the subject of much attention. Quantum games are interesting because classical game theory (CGT) is a well understood discipline (with many applications in economy, psychology, and biology [13,14]). Thus, quantizing it has provided rewarding insights. Many physics' problems can be regarded as games. An example is quantum cryptography, easily cast as a game between individuals who wish to communicate and those who wish to eavesdrop [2]. An area of much interest, quantum cloning, has been recast in terms of a physicist playing a game against nature [3]. Most importantly, the measurement process itself may be viewed in such manner. Meyer [5] has pointed out that algorithms devised for quantum computers can be regarded as games between classical and quantum agents. Other games are expressed in terms of a quantum computer and its operator. As stated by Benjamin and Hayden [7], against this background, it is natural to seek a unified theory of games and quantum mechanics".
We will reformulate elementary notions of game theory (GT) in the parlance of quantum theory, which may be also thought of as an interpretation of a physical process in GT-terms. We will focus attention on the semi classical case that has a long history.
Semi classical approximations to quantum mechanics constitute an indispensable tool. Even with the present computer technology, exact numerical solutions for the Schrodinger equation are unattainable in most cases and exist mostly for problems with a few degrees of freedom. Moreover, the semi classical approximation facilitates an intuitive understanding usually hidden in brute-force numerical solutions of the Schrodinger equation. The semi classical field is continuously evolving. There still exist many open problems in the mathematical aspects of the approximation as well as in the search for new ways to apply it to physical systems [15,16].
The picture we have in mind was developed [11]: an open quantum system corresponding to a biophysical Hamiltonian is regarded as a quantum game, although our subject is very different. We view the temporal evolution of a semi classical system as a game and the concomitant associated process is transcribed in terms of strategies involving players that look for ways to optimize their chances.
From the study by Kowalski and Plastino [17] we toyed with the idea de expressing physical model in game-theory parlance by considering the interaction between matter and a single-mode of an electromagnetic field. The associated game admits both classical and quantal players and strategies are determined by the initial conditions of the pertinent dynamical system. More specifically, from the study by Kowalski and Plastino [17] we considered states in the way Meyer does [5] with regards to quantum coins. Instead, from the study by Kowalski and Plastino [18] we have looked at the same physical scenario, but limiting ourselves to orthogonal initial states, which is tantamount to saying that they are distinguishable. Remarkably enough it has been seen that this merely technical detail profoundly modifies the whole picture.
Basic notions
In a game we deal with
• a finite set of N players plus a set of pure strategies si (i=1, 2…, N) available to those players.
• pure strategies providing a complete definition of how a player will play. In particular, they determine the moves a player will make for any situation she could face.
• a set of payoffs for each combination of strategies. Payoffs are numbers which rep- resent the motivations of players. Payoffs may represent profit, quantity, utility, or other continuous measures (cardinal payoffs), or may simply rank the desirability of outcomes (ordinal payoffs). In all cases, the payoffs must reflect the motivations of the particular player.
Games admit as well mixed strategies that are combinations of probability assignments to each available pure strategy. If si={si1, …, sik}, a mixed strategy for player i is a probability distribution pi=(pi1,…, pik), where pi1 + .. + pik=1. The payoff Pi is here replaced by an average payoff<P>.
Nash Equilibrium
Suppose that the theory makes a unique prediction about the strategy each player will choose. In order for this prediction to be correct, it is necessary that each player be willing to choose the strategy predicted by the theory. Thus, each player's predicted strategy must be that player's best response to the predicted strategies of the other players. Such a prediction could be called strategically stable, because no single player would want to deviate from her predicted strategy. This situation is called Nash equilibrium. The mixed strategies (p*1,…, p* N) attain Nash equilibrium if, for each player i, pi is player i's best response to the mixed strategies specified for the N-1 remaining players, (p*1,…, p*i-1; p*i+1 ,...,p*N ). Thus,
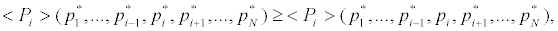 (1)
(1)
for every feasible strategy pi
In quantum games expected payoffs will be calculated now via a density matrix ρ,
Tr (ρ Pi),
where Pi standing for a convenient “payoff” operator associated to each player (quantum and classical) and in general a mixed density matrix
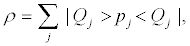
Where 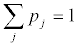 We will call “classical” those players who choose probabilities pj (mixed strategies). “Quantum players”, instead, select quantum states |Qj>as their strategies.
We will call “classical” those players who choose probabilities pj (mixed strategies). “Quantum players”, instead, select quantum states |Qj>as their strategies.
The players need not be human beings. They are basically sets de strategies and payoffs. Our interest here lies in casting physical problems in game-theoretic terms. In particular, our focus is the one described below.
Two level systems
We consider now the following two-level boson Hamiltonian [19,20].
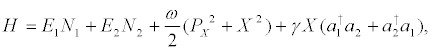 (4)
(4)
that represents matter interacting with a single-mode of an electromagnetic field within a cavity. One has 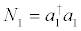 and
and 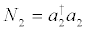 , the population operators corresponding to the levels one and two, respectively, and we assume E2>E1. Here
, the population operators corresponding to the levels one and two, respectively, and we assume E2>E1. Here 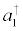 , a1 and
, a1 and 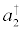 a2, a2, are the creation and annihilation operators of a boson in the levels one and two, respectively. The electromagnetic field, regarded as classical, is represented by the variables (classical) X and PX (X's conjugate momentum) [21,22].
a2, a2, are the creation and annihilation operators of a boson in the levels one and two, respectively. The electromagnetic field, regarded as classical, is represented by the variables (classical) X and PX (X's conjugate momentum) [21,22].
The dynamical equations for the associated quantal variables are the canonical ones [19,23], i.e.,
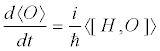 (5)
(5)
Additionally, classical variables obey dissipative equations. We set [19,20]
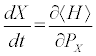 (6a)
(6a)
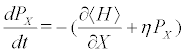 (6b)
(6b)
The energy is taken here to coincide with the quantum expectation value of the Hamiltonian. Consequently, the classical equations of motion to be used here are well-defined one [20]. Taking the set 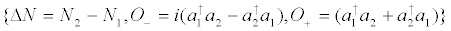 , where we have introduced the population difference operator ΔN, and applying (5) we obtain ( =1) the following Bloch-like equations
, where we have introduced the population difference operator ΔN, and applying (5) we obtain ( =1) the following Bloch-like equations
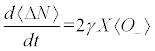 (7a)
(7a)
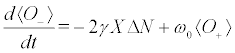 (7b)
(7b)
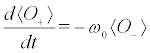 (7c)
(7c)
with 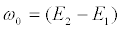 . The mean value
. The mean value 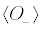 represents a “current” vector and
represents a “current” vector and 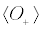 is the expectation value of the quantal factor of the interaction potential. For the classical variables we obtain
is the expectation value of the quantal factor of the interaction potential. For the classical variables we obtain
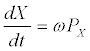 (8a)
(8a)
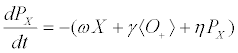 (8b)
(8b)
Each level's population, 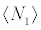 and
and 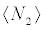 , can be obtained in the fashion:
, can be obtained in the fashion:
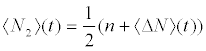 (9a)
(9a)
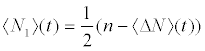 (9b)
(9b)
Where 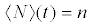 , with n the total number of particles, as N=N1 + N2 is an motion-invariant of the system. We can also define the Bloch-like quantity IB as
, with n the total number of particles, as N=N1 + N2 is an motion-invariant of the system. We can also define the Bloch-like quantity IB as
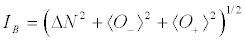 (10)
(10)
which is also an invariant of the motion.
Physical problems as games
Equation (6b) guarantees the existence of attractors [19,20]. Such a fact allows us to think of a game whose results are in correspondence with the end-points of the trajectories that eventually reach one of these attractors. Bets are placed on which attractor will “prevail”. One assumes that players are aware of the details of the underlying dynamical process, i.e., they are cognizant of (4). Thus, the only freedom of choice refers to the initial conditions for the system given by (7) and (8). A pivotal role is then played by the initial version of the density matrix given by Equation (3).
We face here a complete-information game. Each player knows all possible strategies and payoffs. These strategies and payoffs can be made following specified rules, each distinct set of rules leading to a different game, all of them for the same Hamiltonian. In the Literature quantum players make use of qubits and classical ones of bits [4,5,7]. In particular, Meyer [5] considers density matrices of the type (3). Moves that reflect quantum strategies are represented by unitary operators and classical strategies are of a mixed character. Expected payoffs are calculated via the density matrix (3) using the expression (2). The necessary calculations are performed at the attractors' locations for the pertinent initial values, as detailed below in Sect. IV.
We consider the five-dimensional space determined by 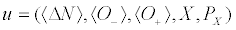 . The fixed points or equilibrium points (labeled by the sub index f) of our system of non-linear equations can be classified as being of type A or B, respectively, according to whether its
. The fixed points or equilibrium points (labeled by the sub index f) of our system of non-linear equations can be classified as being of type A or B, respectively, according to whether its
X-value vanishes or not. Using the invariant IB we obtain [19,20].
Type A:
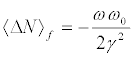 (11a)
(11a)
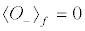 (11b)
(11b)
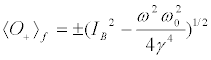 (11c)
(11c)
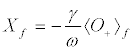 (11d)
(11d)
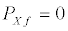 (11e)
(11e)
if 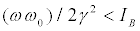
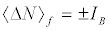 (12a)
(12a)
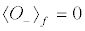 (12b)
(12b)
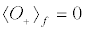 (12c)
(12c)
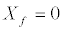 (12d)
(12d)
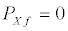 (12e)
(12e)
Studying the stability of these fixed points we can ascertain that those of Type A are stable [19,20], while those of Type B are stable only when 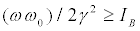 together with
together with 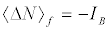 . The stable fixed points are the only attractors of the system (see the detailed investigation of) [19]. In this stability-instance, the final population distribution is originated by a flux from the upper to the lower level, independently of the initial conditions, and of the values of the H-parameters. Instead, for the unstable solution, the ux runs towards the upper level, but for this to happen we need that at the initial time the system has to be already found at the fixed point, where of course it remains forever.
. The stable fixed points are the only attractors of the system (see the detailed investigation of) [19]. In this stability-instance, the final population distribution is originated by a flux from the upper to the lower level, independently of the initial conditions, and of the values of the H-parameters. Instead, for the unstable solution, the ux runs towards the upper level, but for this to happen we need that at the initial time the system has to be already found at the fixed point, where of course it remains forever.
Type B points minimize the quantum energy as well as the total energy. Instead, for Type A only the total energy is minimized, allowing for the quantum energy part to be either increased or not, depending on the initial conditions and on the parametervalues. This fact allows for the final boson-number of the upper level to be greater than the initial one, i.e.
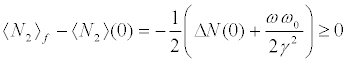 (13)
(13)
which can happen for
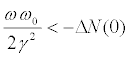 (14)
(14)
with ΔN(0) < 0 .
Expected payoffs
On the basis of (13) we dene a game with two options and two players: the populations of each level either increase or decrease, with the following expected payoffs:
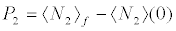 (15a)
(15a)
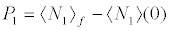 (15b)
(15b)
that can be recast in the form (2) as 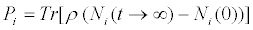 [20] Using (9) we have
[20] Using (9) we have
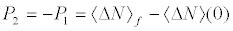 (16)
(16)
so that we face a zero-sum game, whose physical counterpart is boson-number conservation. Henceforth we need to x attention only on P2. According to the stable point character (A or B) we get
Type A
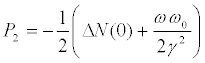 (17)
(17)
If 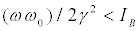 Of course,
Of course,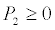 , if (14) is verified
, if (14) is verified
Type B
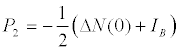 (18)
(18)
if 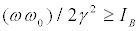 In the last case we always have
In the last case we always have 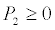 . We remark that, of course,
. We remark that, of course,
if initially the system is at any fixed point, including those unstable of the type B, it will remain there and P2=P1=0. Also, the validity-ranges and the payoffs do not depend on the values of the classical variables X and PX. We proceed next to determine under which initial conditions the system ends-up in one or the other of the two attractors.
Initial conditions' role
The density matrix (3) may represent a game played i) by classical players if we keep fixed the |Qj>-states), ii) between quantum players if p1=1 and the remaining pj vanish, and iii) between both classical and quantum players. If there are several players, the probabilities pj are expressed as products (of probabilities) and the states |Qj>as tensor products of quantum states.
We now specialize (3) to the case of the two levels-system (Cf. Eq. 4). We consider the illustrative instance in which a classical C-player and a quantum Q-one play with two different strategies: a mixed one for player C and a quantum strategy for player Q. Matrix (3) expresses a situation in which C-players support with probability pj (o reject with probability 1pj) the |Qj >-strategy.
For this scenario, Meyer's approach [5] regarding quantum coins was applied in [17] In Meyer's setting; a coin was placed within a box, heads-up initially. The coin is manipulated in three (alternate) occasions by the two players. By C just once. The Q-player wins if the penny is heads up when the x is open for all to see. C supports Q's strategy with probability p \leave the coin untouched" and 1 p \reverse the coin state" [5]. The above setting was slightly generalized in (17), as follows: Let the general initial state be
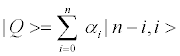 (19)
(19)
with 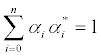 Vectors |n-i, i>, represent states with n-i bosons downstairs and i particles in the upper level. They constitute a basis in the pertinent Fock-space. If Q chooses the strategy
Vectors |n-i, i>, represent states with n-i bosons downstairs and i particles in the upper level. They constitute a basis in the pertinent Fock-space. If Q chooses the strategy 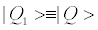 of (19), the alternative strategies are given by the set of vectors
of (19), the alternative strategies are given by the set of vectors
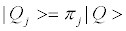 (20)
(20)
with πj operators that, acting on |Q >, produce all possible permutations among the i, generating (n +1)!quantal strategies These operators can be written as 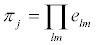 with the elm being “elemental” operators that exchange αl with αm. We are led to
with the elm being “elemental” operators that exchange αl with αm. We are led to
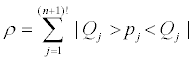 (21)
(21)
with 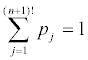 . Here
. Here 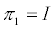 , the identity permutation (|Q1>=|Q>). Eqs. (19) and (20) state that quantum strategies are represented by qubits for n=1 (as in [5]), qutrits for n=2, and, in general, by qunits if we deal with n bosons. Neither Q nor C know what her rival plays. Although the game may be either of sequential or simultaneous nature, it is here more natural to regard it as sequential, with the Q-player making the first move. The matrix version of (21), in terms of the matrix versions of the operators πj , reads
, the identity permutation (|Q1>=|Q>). Eqs. (19) and (20) state that quantum strategies are represented by qubits for n=1 (as in [5]), qutrits for n=2, and, in general, by qunits if we deal with n bosons. Neither Q nor C know what her rival plays. Although the game may be either of sequential or simultaneous nature, it is here more natural to regard it as sequential, with the Q-player making the first move. The matrix version of (21), in terms of the matrix versions of the operators πj , reads
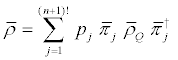 (22)
(22)
Where 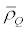 corresponds to the pure operator
corresponds to the pure operator 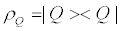 Matrices
Matrices 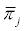 can in turn be cast in the fashion
can in turn be cast in the fashion 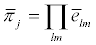 i.e., in terms of the elemental matrices
i.e., in terms of the elemental matrices 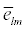 that arise out of interchanging rows l and m in the identity matrix. Classical strategies (in) are represented by the choice of the
that arise out of interchanging rows l and m in the identity matrix. Classical strategies (in) are represented by the choice of the 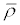 , together with the operations implied by the matrices
, together with the operations implied by the matrices 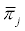 . The states (20) are not distinguishable, so that
. The states (20) are not distinguishable, so that 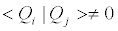 . We introduce next a one-boson game that involves distinguishable, i.e., orthogonal states and overlapping ones.
. We introduce next a one-boson game that involves distinguishable, i.e., orthogonal states and overlapping ones.
A bosonic game
Let us discuss in more detail the n=1-instance of one Q-player and one C-one, since this is already enlightening enough, as will be seen. The density operator is
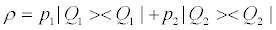 (23)
(23)
with p1 + p2=1. |Q1>- |Q2>are n=1-qubit-states (20) (17)
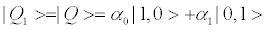 (24a)
(24a)
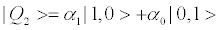 (24b)
(24b)
where 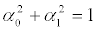 We have taken α0 y α1 to be real, without loss of generality. |1,0> stands for our particle being downstairs, and vice-versa for |0,1>. If we wish that our protagonists be orthogonal-states we need [18]
We have taken α0 y α1 to be real, without loss of generality. |1,0> stands for our particle being downstairs, and vice-versa for |0,1>. If we wish that our protagonists be orthogonal-states we need [18]
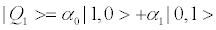 (25a)
(25a)
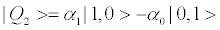 (25b)
(25b)
where 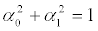 (again, we have taken α0 y α1 to be real). Thus, the density matrix adopts here the appearance [18]
(again, we have taken α0 y α1 to be real). Thus, the density matrix adopts here the appearance [18]
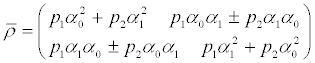 (26)
(26)
where the sign correspond to the states given by (24) and (25), respectively.
We assume now that the C-player places his bet on that the upper level will increase its population for t → ∞ . This is a priori, the un-likeliest choice. The ensuing payoff will be P2. For P2>0 the C-player wins and vice-versa for P2<0. Using (26) we find, associated to the type of fixed point (A or B) under scrutiny, the pertinent payoffs (see (17)-(18)). For the states (24) one gets:
Type A
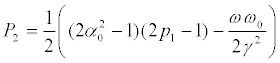 (27)
(27)
If 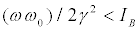
Type B
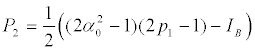 (28)
(28)
If. 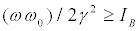 . In this case the invariant IB reads
. In this case the invariant IB reads
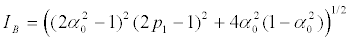 (29)
(29)
Now, if we consider instead the orthogonal states (25), we find
Type A
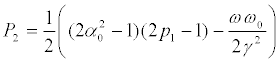 (30)
(30)
if 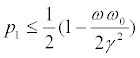 or
or 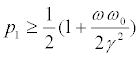
Type B
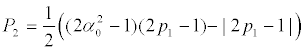 (31)
(31)
if 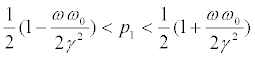 . Here IB=|2p1-1|
. Here IB=|2p1-1|
In order to gain intuitive understanding we would need to consider the game's version that uses only pure strategies [1]. The first player bets on one of the two levels and places a particle there. A third party (referee) asks the second player (who ignores what choice has been made before) whether she wishes to change or support her partner's bet. Afterwards, the system evolves and ends up in one of the two levels. If the first player bet on level 1, his payoffs would be 1, -1, or 0 according to whether the boson has descended, climbed, or remained in the original place. Since strategies (mixed ones) can be followed using bettingprobabilities, these lead to an appropriate expected payoff [1]. Now, if first player follows a Q-strategy, in the n=1 instance this strategy is represented by a qubit and we are led to the expected payoff computed according to (2) which leads to either (27) or (28).
Some interesting results
Some results concerning the just discussed issues are illustrated in Figures 1 and 2. We chose as independent parameters 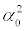 and p1. Since we wish for the existence of the two types of fixed points for n=1, one needs that
and p1. Since we wish for the existence of the two types of fixed points for n=1, one needs that 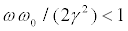 . We set
. We set 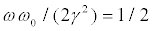 .
.
Figure 1. Classical probability p1 vs. quantum probability α20 for the states (24). We set ωω0/(γ2)=1/2 . Regions corresponding to the fixed points of types A and B are separated by solid lines representing the curve IB =ωω0/(2γ2) ,with IB given by (29). Regions corresponding to the zones in which the C-player either wins or loses are separated by dotted lines (where P2=0) given by Eq. (32). The payoffs P2 are given by Eq. (27) or (28), for Type A or B, respectively. We also can observe a single Nash equilibrium point for p1 =1/ 2 y α20=1/2 (denoted as N).
Figure 2. Classical probability p1 vs. quantum probability α20 , as in Figure 1, but for the states (25). We set ωω0/(2γ2) =1. Regions corresponding to the fixed points of types A and B are separated by solid lines representing the curves p1 = (1/ 2)(1−ωω0 / 2γ2 ) and p1 = (1/ 2)(1+ωω0 / 2γ2 ) . Regions corresponding to the zones in which the C-player either wins or loses are separated by dotted lines (where P2=0) given by Eq. (32), as in Fig 1. The dotted line p1=1/ 2 corresponds to P2=0. The payoffs P2 are given by Eq. (30) or (31), for Type A or B, respectively. This second plot is simpler than that illustrated by Fig. 1. In this case we observe a continuum of Nash equilibrium points for p1 =1/ 2 and (1/ 2)(1-ωω0 / 2γ2 ) ≤α20 ≤ (1/ 2)(1+ωω0 / 2γ2 ) (denoted as N).
In Figure 1 we display results for the states (24). The regions corresponding to each type of fixed point (A and B) are separated by the curve 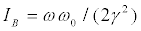 (solid), with IB given by (29). Zones in which the Q-player either wins or loses are also well-delimited [24,25]. The payoffs
(solid), with IB given by (29). Zones in which the Q-player either wins or loses are also well-delimited [24,25]. The payoffs
P2 are given by Equations (27) or (28), for Types A or B, respectively. The dotted curve is in this case a “separator”, being given by
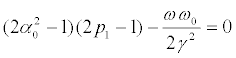 (32)
(32)
that one get s by setting P2=0 in (27).
Of outstanding importance is the existence of a unique Nash equilibrium point regarding classical/quantal best responses: p1=1/2 and 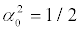 , respectively (denoted as N). This result mimics the one found for a classical Meyer game of “Penny Flip over” [5], after two rounds. The C-player bets with equal probability on both the Q-strategy and its opposite one. At the same time, the Q-player's strategy (unknown to the C-one) bets evenly on the two alternative options of placing the particle up- or downstairs [26].
, respectively (denoted as N). This result mimics the one found for a classical Meyer game of “Penny Flip over” [5], after two rounds. The C-player bets with equal probability on both the Q-strategy and its opposite one. At the same time, the Q-player's strategy (unknown to the C-one) bets evenly on the two alternative options of placing the particle up- or downstairs [26].
In Figure 2 we display results corresponding to states (25). Regions corresponding to the xed points of types A and B are separated by solid lines representing the curves 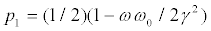 and
and 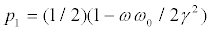 , respectively. Regions corresponding to the zones in which the C-player either wins or loses are separated by dotted lines (where P2=0), given by Eq. (32), as in Figure 1. The dotted line p1=1/2 also corresponds to P2=0. The payoffs P2 are given by Eq. (30) or (31), for Types A or B, respectively. This second plot is simpler than that illustrated by Figure 1 [27-29].
, respectively. Regions corresponding to the zones in which the C-player either wins or loses are separated by dotted lines (where P2=0), given by Eq. (32), as in Figure 1. The dotted line p1=1/2 also corresponds to P2=0. The payoffs P2 are given by Eq. (30) or (31), for Types A or B, respectively. This second plot is simpler than that illustrated by Figure 1 [27-29].
Remarkably enough, a continuum of Nash points emerges now for the best classical response p1=1/2 and the best quantal responses corresponding to 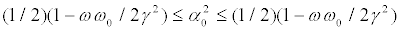 , respectively.
, respectively.
In Figures 1 and 2, the region corresponding to P2>0 is smaller than that for P2<0, but the first one grows (in both cases) also as 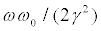 diminishes. The same happens when considering the Type A-region [30]. If
diminishes. The same happens when considering the Type A-region [30]. If 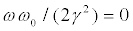 one finds, for both kinds of states (24) and (25), the situation represented in Figure 3. Equal areas are apportioned to the regions (P2<0 and P2>0). Here we encounter only Type A-Fixed Points and a single Nash equilibrium-point at p1=1/2 and
one finds, for both kinds of states (24) and (25), the situation represented in Figure 3. Equal areas are apportioned to the regions (P2<0 and P2>0). Here we encounter only Type A-Fixed Points and a single Nash equilibrium-point at p1=1/2 and 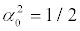 , both for (24)-states and for (25)-ones. This is a very peculiar instance in which either ω = 0 , an extreme situation for which the field exhibits a free-particle dynamics, γ → ∞ (extremely “large” coupling) [31,32].
, both for (24)-states and for (25)-ones. This is a very peculiar instance in which either ω = 0 , an extreme situation for which the field exhibits a free-particle dynamics, γ → ∞ (extremely “large” coupling) [31,32].
Figure 3. Classical probability p1 vs. quantum probability for the special case ωω0/(2γ2) =0 . This plot corresponds to the two type’s state, (24) and (25). Equal areas are apportioned to the regions (P2<0 and P2>0). Here we encounter only Type A - Fixed Points, and a single Nash equilibrium-point at p1 =1/ 2 and α20=1/ 2 , both for (24)-states and for (25)-ones.
We also verify (see Figures 1 and 2) that the strategy corresponding to selecting p1 in such a manner that
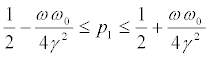
Guarantees that the q-player will win, independently of the classical strategy for both distinguishable and un-distinguishable quantum states. Moreover, if p1=1/2, this holds for any choice of parameters' values. Such “happy” circumstances do not exist for the C-player, no matter what its strategic choice is [33-35].
Our goal has been that of translating aspects of nonlinear dynamics' problems into Games' Theory language, in the hope of getting some degree of enlightenment. Indeed, we have expressed the physics of the semi-classical Hamiltonian (4) in terms of Game Theory [17]. This model represents the interaction between matter and a single-mode of an electromagnetic field within a cavity. The interaction-role is represented as a game between classical and quantum players who bet on initial conditions. The associated dynamics, via the physical system's attractors, is expressed in terms of the game's payoffs [17]. In the present context the boson-number conservation is cast in the guise of a zero-sum game, a result that can be generalized for Hamiltonians other than (4).
No actual human beings need play our game. Any matrix density given by (3) is associated to a mixed strategy that, in turn, implies a classical player. Likewise, any state (3) is associated to a quantum strategy, and thus to a quantum player. Initial states play a critical role, as they represent our quantum player's strategies. Here we have dealt with initial states of the type (24) [17], following Meyer's approach [5], or with orthogonal states given by (25) [18], that are distinguishable on that account.
Surprising insights ensue after comparison of the pertinent results that have been pointed out in the preceding Section. Here we remark on the existence of a continuum of Nash points for orthogonal initial states instead of the single Nash point attached to partially overlapping initial states.
Note that our game is not a mere abstraction. Given that it represents a physical interaction, we can speak of a \real" game (as far as a physical model can be considered real). In this context, any experimentalist can be viewed as a classical player.
The author wishes to thank A. Plastino of IFLP, Fac. de Ciencias Exactas, National University La Plata, Argentina.