ISSN: 2320-2459
ISSN: 2320-2459
1Departamento de F sica, Univ. de Los Andes, 111711 Bogota, Colombia
2Departamento de F sica Teorica II. Univ. Complutense. 28040 Madrid. Spain
3Departamento de F sica, Univ. Nacional de Colombia, 111321 Bogota, Colombia
Received Date: 08/02/2017; Accepted Date: 17/02/2017; Published Date: 24/02/2017
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
In this work, we discuss and summarize three large N approaches given to analyze how a set of massless pions behave at nite temperature. The first one focuses in the problem of obtaining thermal phase shifts, where the others aim to study chiral symmetry restoration phenomena. All the results are achieved by considering an O(N + 1)/O(N) nonlinear sigma model where N is the number of pions (or Nambu-Goldstone bosons) involved, in which thermal e ects are introduced via the imaginary time formalism.
Chiral lagrangians, Finitetemperature field theory, Large N expansions, Chyral symmetries
Low-energy critical phenomena such as chiral symmetry restoration are needed for a better understanding of the behavior of hadronic matter created in relativistic heavy ions collisions (e.g. LHC-ALICE). A very adequate approach with outstanding results is given by lattice simulations [1-4], where physical observables such as chiral critical temperatures and exponents are obtained. Some theoretical advances can be made if and only if they fulfill the conditions given in the low energy regime of QCD, as showed by Chiral Perturbation Theory (ChPT) momentum expansions extended to the nite-temperature regime involving light mesons [5,6], or Nambu - Jona-Laisino (NJL)-like models [7], in which quark fields are taken as the degrees of freedom. These models include an explicit chiral symmetry breaking term that induces mass to the fields involved.
Here we consider a nonlinear sigma model of N self-interacting massless pions and a eld in which a scalar resonance (the f0 (500)) is dynamically generated, thus breaking the chiral symmetry [8,9]. The f0 (500) has the same quantum numbers as a QCD vacuum state, and is susceptible to chiral symmetry restoration e ects. In order to attain this, temperature is introduced via self-energy and scattering loop corrections [10,11], and three approaches are considered in order to study two sort of phenomena: thermal e ects on scattering phase shifts [12] and chiral symmetry restoration through scattering [13,14] and generating functional developments [15]; in these two last works, we obtain a second-order phase transition after considering a regime where the temperature is below its chiral critical value T 150 160 MeV.
We begin by considering a O(N + 1)/O(N) nonlinear sigma model for massless pions whose Lagrangian reads [8,9]
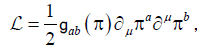 (1)
(1)
Where the vacuum constraint and metric induced by it read, respectively,
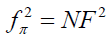 (2)
(2)
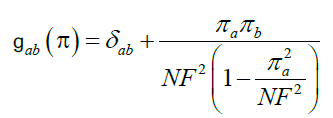 (3)
(3)
The scattering Feynman rules and diagrams are obtained after expanding the non-diagonal term in (3), thus yielding the results shown in Figure 1.
All the scattering rules are written in terms of the Mandelstam variables.
We can consider among three approaches to analyze Finite-Temperature pion phenomena in the chiral limit:
1. Isolating the 4-pion vertex and separating the dynamics at zero and nite temperature so thermal phase shifts can be studied.
2. Building up an effective interaction vertex with all the tree-level diagrams and dynamically generate a scalar resonance (σ/f0 (500)); since this resonance is associated to chiral symmetry breaking, thermal effects will allow us to check whether this symmetry is to be (or not to be) restored.
3. Introducing an explicit symmetry breaking term in such a way that a very small pion mass is generated. As in the previous item, we will study restoration of broken symmetries, although using a diagrammatic analysis for partition functions.
1ST Approach: Dynamics of Massless Pions at Finite Temperature
We build up an effective Thermal Vertex (ETV) as it is shown in Figure 2: here we close every pair of extra pion lines that come from the 1/N expansion of the nonlinear metric (3) in such a way that only four external legs are involved. All the closed ring diagrams correspond to tadpoles whose contribution is N Iβ . This allows us to take into account any effect associated to the presence of a thermal bath in the scattering dynamics, something that we schematically exhibit in the diagrams of Figure 3, where we label the scattering amplitudes as [l;m]; in this case, l is the number of ETV's considered and m indicates if there is any initial scattering loop (as it is shown in the diagram for [2; 1]).
Since pion are massless, we do not have to deal either with mass or wave function renormalization1; instead of these, the divergence comes from the scattering loop integral Iβ(S), whose explicit dimensionally regularized form reads
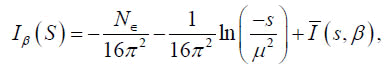 (4)
(4)
and where the thermal (and finite) contribution is given by
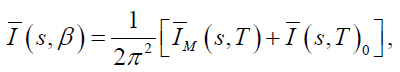 (5)
(5)
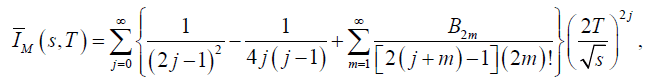 (6)
(6)
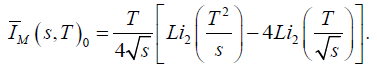 (7)
(7)
In this case, is the renormalization scale of the loop integral (4), whilst B2m are Bernoulli numbers and Li(x) is the logarithm integral function? We obtained the latter nite-temperature results by considering that the energy of the pions of the loops E is such that E < √s and E < T, where T is the temperature of the thermal bath [12-17]. The renormalization is attained after redefining both the four-pion and the ETV as follows:
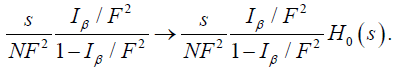 (8)
(8)
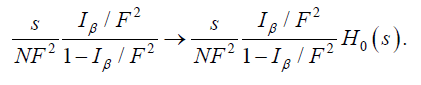 (9)
(9)
G0(s) and H0(s) are bare couplings whose function is to absorb the pole given in (4), as shown below:
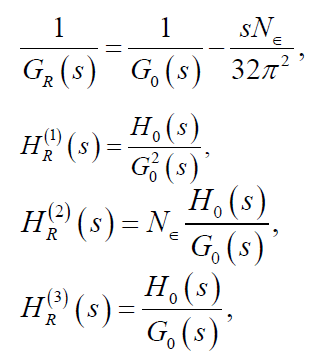 (10)
(10)
Where N∈ is a divergent quantity defined in the renormalization MS scheme. Thanks to this, we can write a finite (renormalized) amplitude AR (s,β) such that
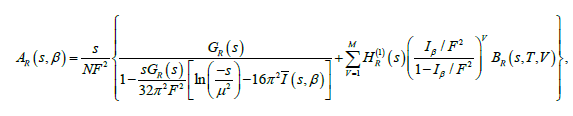 (11)
(11)
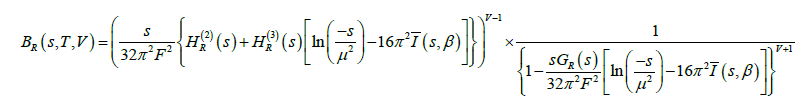 (12)
(12)
After expanding the scalar channel I=J=0 amplitude 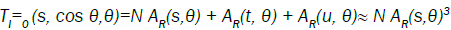 in partial waves (considering the lowest order approximation:
in partial waves (considering the lowest order approximation: 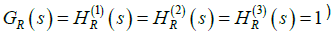
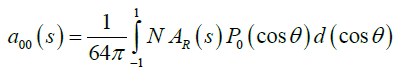 (13)
(13)
We obtain the thermal phase shifts showed in Figure 4. As it can be seen, they monotonically increase as both the COM energy √s and the temperature T are enlarged [18-24].
Unfortunately, this approach has the following issues:
The renormalization procedure has a problem with the definition of 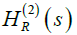 and
and 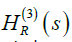 because
because 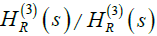 →∞. In order to renormalize properly these quantities, another bare coupling constant has to be added to the equation set 10, as
shown for the massive case in ref. [8].
→∞. In order to renormalize properly these quantities, another bare coupling constant has to be added to the equation set 10, as
shown for the massive case in ref. [8].
The finite-temperature integral 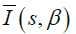 violates unitarity. The nonlinear sigma model is already unitarized in the energy range
300 MeV ≤ √s ≤ 700 MeV since the scalar resonance σ/f0 (500) is considered in the dynamics.
violates unitarity. The nonlinear sigma model is already unitarized in the energy range
300 MeV ≤ √s ≤ 700 MeV since the scalar resonance σ/f0 (500) is considered in the dynamics.
Both F and μ are not appropriate values to this chiral model. The values we consider are given for a massive nonlinear sigma model. In that case, (F,μ )=(55; 775) MeV [8].
All these problems are properly fixed in the next section.
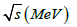
2nd Approach: The f0 (500) and Chiral Restoration
We de ne a new ETV by including the four pion term of Figure 1 (the one without extra lines); this corresponds now to replace the function in Figure 2 by
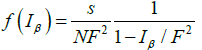 (14)
(14)
In this case, we separate the dynamics at zero and nite temperature by building two amplitudes: the first one where thermal bath effects are not considered, and the second one which introduces temperature thanks to (14) and to the thermal loops J(p;T) in it, as shown in Figure 5. In this case, J(p;T)4 reads
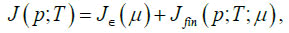 (15)
(15)
Where Jfin(p;T;μ) also includes the zero-temperature finite term given by
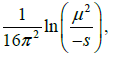 (16)
(16)
and the divergent term is given in dimensional regularization as [18]
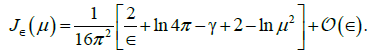 (17)
(17)
The renormalization of the amplitudes A(s) and A(p;T) in Figure 5 is adequately attained after redefining the vertices as 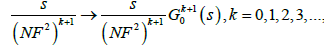 thus yielding a finite coupling GR(s,μ) such that:
thus yielding a finite coupling GR(s,μ) such that:
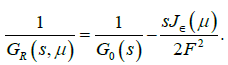 (18)
(18)
Since the partial wave decomposition 13 is also valid at nite temperature, we can check that this model holds exactly with
unitarity in this regime (a fact that was imposed in the usual momentum expansion [24]). This allows us to check if the chiral symmetry
is restored at a given value of temperature, something easily achieved after finding the resonance/pole in the second Riemann sheet by
extending the energy to the complex plane as √s(T)=MP (T )− iΓP (T )/2, and by defining a proper quantity such as the scalar susceptibility,
whose behavior in the p=0 limit is 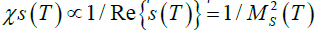 and its unitarized form reads [16]
and its unitarized form reads [16]
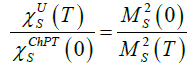 (19)
(19)
The behavior of (21) (taking into account our ts for the parameters, along with the IAM result in the chiral limit [16]) is shown in Figure 6, and our results concerning resonance position in the complex plane (mass and width), critical temperatures and critical exponents for χS(T) are given in Table 1 [13,14].
Table 1. Resonance positions in the complex plane and critical temperatures and exponents for the scalar susceptibility χs(T).
| Fit | Tc (MeV) | MP (0) (MeV) | ΓP (0) (MeV) | gc | 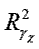 |
|---|---|---|---|---|---|
| Grayer | 92.33 | 438.81 | 536.47 | 0.875 | 0.99987 |
| Peláez 1 | 96.00 | 452.42 | 546.26 | 0.938 | 0.99997 |
| Peláez 2 | 129.07 | 535.53 | 534.59 | 0.919 | 0.99995 |
| IAM | 118.23 | 406.20 | 522.70 | 1.012 | 1 |
| Standard | 61.20 | 356.97 | 566.05 | 0.842 | 0.99728 |
Due to the lack of experimental data, we compare our Tc and γχ values with the lattice values Tχ=154± 9 MeV [2] and γχ=0.54 (three-dimensional O(4) model) [3], along with the theoretical four-dimensional O (N→∞) model γχ=1 [25]. In this case, T is expected to decrease about 20% of its value. As it can be seen, our results agree with these bounds. In the other hand, our resonance parameters MP (0) and ΓP (0) are in good accordance with the most recent experimental bounds [26] and with the theoretical fit [23], where 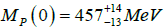 and
and 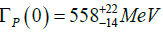 .
.
The reach of this works ends here, because order parameters as the scalar quark condensate (whose derivative in terms of the mass yields the scalar susceptibility χs (T ) ) cannot be found by taking the strict chiral limit. This is the aim of the next section.
3rd. Approach: Large-N Partition Function for Massless Pions
All we have to do so mass is to be considered is adding a massive term to the Lagrangian (1) (as shown in ref. [8]), i.e.,
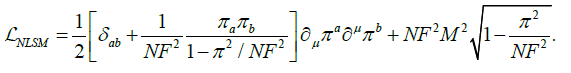 (20)
(20)
After expanding the square root term in (22), we build an effective mass vertex as that given in Figure 7. Then, we construct
the partition function as shown in Figure 8, where only the contributions given up to order 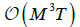 are to be taken into account
when considering the limits M/F, M/T→0 (any higher contribution induces mass divergences, something we want to avoid since
their large N resummation becomes harder). Its explicit dependence on M, T and N is such that:
are to be taken into account
when considering the limits M/F, M/T→0 (any higher contribution induces mass divergences, something we want to avoid since
their large N resummation becomes harder). Its explicit dependence on M, T and N is such that:
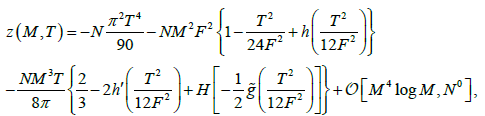 (21)
(21)
Where the finite functions g(x), h(x) and H(x) are given by:
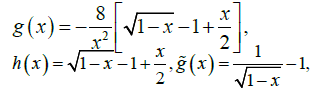 (22), (23)
(22), (23)
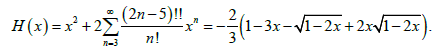 (24)
(24)
Since we are keeping a finite mass-dependent partition function, we can derive it in order to obtain the scalar quark condensate
and take the chiral limit to check if there is an associated critical temperature, as it was made for the scalar susceptibility in
section IV. The result normalized to 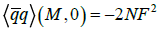 explicitly reads
explicitly reads
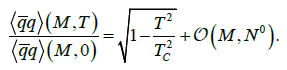 (24)
(24)
We plot the normalized condensate (26) as a function of T in Figure 9 [15], along with the results for the ChPT momentum expansion to different perturbative orders [5]. Here we obtain exact critical exponent β=0.5 (and a critical temperature 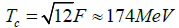 when taking the standard values for (F,μ)-), something that cannot be found in ChPT since the scalar condensate is a polynomial in the temperature.
when taking the standard values for (F,μ)-), something that cannot be found in ChPT since the scalar condensate is a polynomial in the temperature.
We have reviewed some recent approaches to chiral symmetry restoration within the large-N effective theory approach for the pion gas. Our first approach yields some inconsistencies related with unitarity and renormalization
Properties of the nonlinear sigma model; this made us reconsider how to build quantities as scattering amplitudes in such a way that those issues are to be avoided.
In our second approach, the analysis of elastic pion scattering at finite temperature in the large N expansion grants a description of the fo(500) resonance dependence on T that is consistent with previous works [16]. Furthermore, there are two aspects to point out:
1. The behavior of 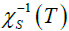 when considering saturation by the fo(500) pole, is consistent with a second-order phase transition,
as seen in the lattice [2].
when considering saturation by the fo(500) pole, is consistent with a second-order phase transition,
as seen in the lattice [2].
2. Our Tc results are not far from the expected lattice values (as explained in section IV), and besides, they are even closer to the result obtained for NJL-like models (Tc≈100.7 MeV.) [26].
We show in our third approach that scalar quark condensates can be obtained through a large N partition function, which is indeed finite since the mass divergences do not appear in the limits M/F, M/T 0. Furthermore, our critical exponent β is found in an exact way, and coincides with the expected value for an O(N)-symmetric 4-dimensional Heisenberg model (a fact also checked in section IV) [25]. Nevertheless, the critical temperature is quite higher than in the scattering analysis; this is due to not considering the saturation of the fo (500) resonance.
We expect to use another approaches, e.g., the virial expansion (S. Cortés, A. Gómez Nicola and J. Morales –in preparation-) and holographic models (S. Cortés, M. A. Martín Contreras and J. R. Roldán -in preparation-), so a broader map can be built to compare these sort of critical phenomena.
S.C. and J.R.R. thank Departamento de Física - Uniandes and Facultad de Ciencias - Uniandes for financial support. A.G.N. acknowledges financial support from the spanish research contracts FPA2014-53375-C2-2-P and FIS2014-57026-REDT.