ISSN: 2322-0066
ISSN: 2322-0066
Samuel Bonaya Buya*
Department of Mathematics/Physics, Ngao Girls Secondary School, Kenya
Received date: 28/07/2017; Accepted date: 25/09/2017; Published date: 30/09/2017
Visit for more related articles at Research & Reviews: Research Journal of Biology
I prove that the general quintic equation is solvable in radicals. Here solvability in radicals is loosely used to mean root form of the quintic equation even though there may be cases formula for the equation may result in a rational root. I re-examine Abel-Ruffini theorem in the light of Galois Theory in order to highlight some avenues possibilities and loopholes not thoroughly explored in arriving at the theorem. I show that the general quintic equation has a solvable Galois group. Proof of solvability in radicals comes down to computing the Galois group of the general quintic equation and showing that it is solvable. Since S5 is the Galois group of the quintic equation I will show and demonstrate that the quantities used to construct it are as a matter of fact algebraically determinate. In the process of proving this I will derive all the roots of the general quintic equation. In so doing I prove the incompleteness of Abel-Ruffini theorem and Galois Theory at large. In attempting to prove the solvability of the general quintic in radicals, a very important principle is discovered governing solution of polynomial equations
Algebra solution General quintic equation; general Abel-Ruffini theorem
Literature review and way forward
For some centuries mathematicians tried to find a method of solving the general quintic equation but in all their effort they did not succeed. The first mathematician who claimed the impossibility of the algebraic solution of the quintic equation was Paulo Ruffini in 1799. Ruffini’s proof did not gain universal acceptance since there was a gap in His proof. In 1824 Niels Henrik Abel presented a proof that was accepted. Later on Evariste Galois came up with a theory which gave a criterion under which an equation was solvable in radicals. The Theorem of Galois states that F(x)=0 is solvable in radicals if and only if G_F is a solvable group.
In this paper I will attempt to present a proof of solvability of the general quintic equation. The end result of this proof can be used to obtain solution of polynomial equations of degree greater than five. I will explore the possibility of coming up with an algebraic solution using the extension of the equation.
Method
I will attempt to present a proof of solvability of a degree five polynomial equation. Here I will assume a field k of characteristic zero. Consider some quantities S1, S2…….S5 algebraically independent over k.
Setting 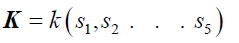 (1)
(1)
And defining
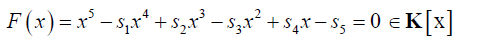 (2)
(2)
If there exists 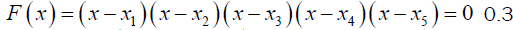 in an extension field of K, then the splitting field S for F(x) over K is given by
in an extension field of K, then the splitting field S for F(x) over K is given by 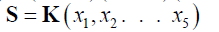 (3)
(3)
By the above definitions we note that Si are the elementary symmetric functions of xisuch that:
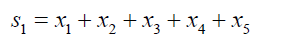 (4)
(4)
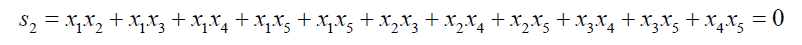 (5)
(5)
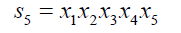 (6)
(6)
Each permutation of xi induces an automorphism on S that does not change K. In modern algebra S/K is a Galois extension with the Galois group isomorphic to S5
Abel’s theorem asserts that for a general equation of degree n over k, n is not solvable in radicals for n ≥ 5 .
Here I will assume solvability in radical to loosely solvability in root form though there may be many cases in which a root may degenerate to rational numbers.
The assertion of insolvability is that for n ≥ 5 , s/k cannot have a radical tower.
In a letter to Crelle dated 18th October 1828 Abel remarked that “If every three roots of an irreducible equation of Prime degree are related to one another in such a way that one of them may be expressed rationally in terms of the other two, then the equation is solvable in radicals.
Abel’s remark is similar to a preposition by Galois that is, “In order for an irreducible equation of prime degree to be solvable in radicals it is necessary and sufficient that once any of the two roots are known, the others can be deduced from them rationally [1].
If in the extension Field K 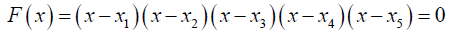 there exists then the following holds:
there exists then the following holds:
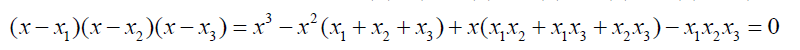 (7)
(7)
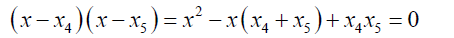 (8)
(8)
The whole essence of this innovative step is dividing the roots into two groups of roots to enhance easy solvability. The first group G1 has three roots and the second group, G2 has two roots
That is the equation 3 can also be written in the form:
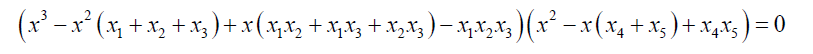 (9)
(9)
Bring [2] and Jerrard [3] showed that the general quintic equation 2 can be reduced to a simple form with two parameters, that is:
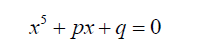 (10)
(10)
For equation 9 to conform to the Bring-Jerrard form (9) it can be written in the form below, see [4]
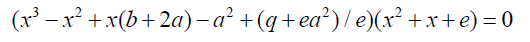 (11)
(11)
In this form: 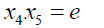 (12)
(12)
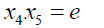 (13)
(13)
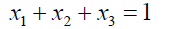 (14)
(14)
Substituting equation 11 into 12 and simplifying:
We obtain the equation:
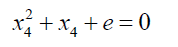 (15)
(15)
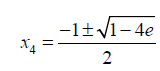 (16)
(16)
If we take 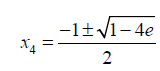 (17)
(17)
Then 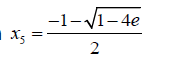 (18)
(18)
From 9 and 11
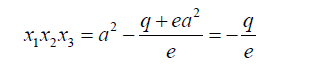 (19)
(19)
Substituting 14 into 19 and simplifying:
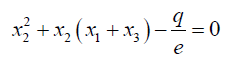 (20)
(20)
From 14:
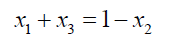 (21)
(21)
Substituting 21 into 20 and simplifying:
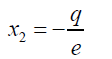 (22)
(22)
Substituting 22 back into 21:
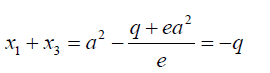 (23)
(23)
Substituting x2, x4 and x5 into 6
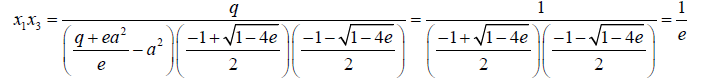 (24)
(24)
Substituting 23 into 24 and simplifying we obtain the equation:
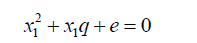 (25)
(25)
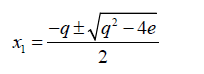 (26)
(26)
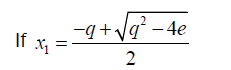 (27)
(27)
Then
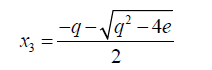 (28)
(28)
For the equation 11 to be reduced to the form to the Bring-Jerrard form then the quantities a, b and e are expressed as functions of p and q, see
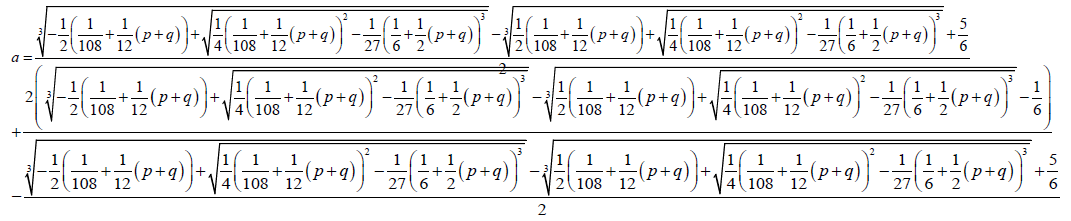 (29)
(29)
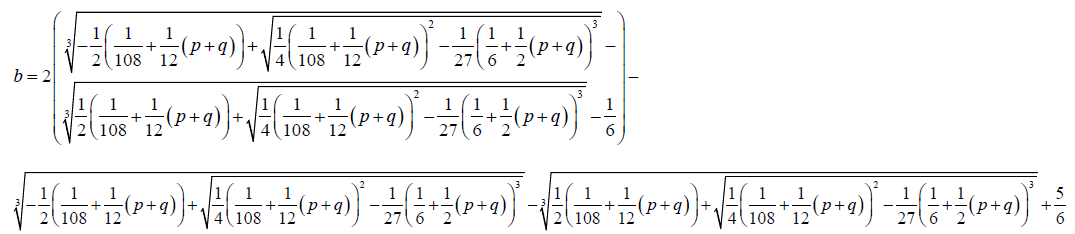 (30)
(30)
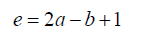 (31)
(31)
To confirm the authenticity of the roots obtained above we can substitute 13 and 19 into 6 and we obtain the following result:
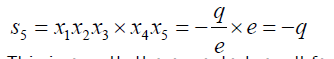 (32)
(32)
This is exactly the expected result for the Bring-Jerrard quintic.
F(x) = 0 is solvable if it has a solvable Galois group, GF. The Galois group of the quintic equation is equal to S5.
The result 32 above confirms the solvability of quintic equations in radicals.
Some important observations and applications
We not in this analysis a very noteworthy principle for a degree five polynomial if the product of three roots is equal to 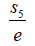 then the product of the other two roots is e. This observation can be extended in general. If this observation is extended to cubic equation with Galois group ÃâÃâ¢3, then if the product of two of roots is say
then the product of the other two roots is e. This observation can be extended in general. If this observation is extended to cubic equation with Galois group ÃâÃâ¢3, then if the product of two of roots is say 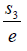 then one of the roots is e. This observation is trivially true but has many applications.
then one of the roots is e. This observation is trivially true but has many applications.
For example consider the cubic equation 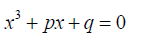 (33)
(33)
If its roots are denoted as x1,x2,x3(34)
Then if 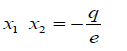 (35)
(35)
Then 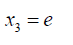 (36)
(36)
From 34 and 35 we note that
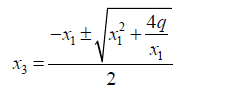 (37)
(37)
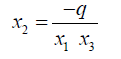 (38)
(38)
In general for a degree n polynomial if the roots are divided into say three groups such that the product of the roots in the three groups is say G1 , G2 ,G3 then the following connection can be used to relate them:
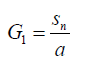 (39)
(39)
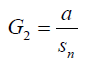 (40)
(40)
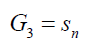 (41)
(41)
Where Sn = G1 G2 G3 and α is a parameter connecting the groups. In group theory sn is the Galois group of an algebraic equation of degree n.
The above Chain rule of Galois connections can be extended to any number of selected groups of roots. The importance of these connections is in the establishment of relationships between roots as demonstrated in 33 to 37. These connections are of importance in establishing formulae of higher degree polynomials subject to other considerations.
The general quintic equation is solvable in radicals. The construction of Abel impossibility theorem did is incomplete in the sense it omitted several possibilities of obtaining radical solutions from the field extension. Galois Theory did not provide a way forward in providing a general solution to degree five polynomials and above but it can be modified to take into account solvability of higher degree algebraic equations.