ISSN: 2320-2459
ISSN: 2320-2459
1Federal Polytechnic, Auchi, Nigeria
2Delta State University, Abraka, Nigeria
Received Date: 11/10/2017; Accepted Date: 09/11/2017; Published Date: 29/11/2017
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
In this paper the modified Landau theory of Fermi Liquids was used to compute thermal expansion and thermal conductivity of quasi-particles in metals. The result revealed that as temperature increases the thermal expansion of quasi-particles in metals increases in all the metals investigated. It is also observed that as the electron density parameter increases the thermal expansion of quasi-particles increases. This shows that at low density region the thermal expansion of quasi-particles is large. The result obtained for the thermal conductivity of quasi-particles in metals revealed that for all the metals computed the thermal conductivity of quasi-particles decreases as temperature increases. This seems to suggest that as temperature increases the separation between quasi-particles increases because they are not heavy particles hence, the rate of absorbing heat decreases. The computed thermal expansion and thermal conductivity of quasi-particles are in better agreement with experimental values. This suggests that the introduction of the electron density parameter is promising in predicting the contribution of quasi-particles to the bulk properties of metals. This study revealed the extent to which quasi-particles contribute to the bulk properties of metals, which assisted their potential applications in materials science and engineering development.
Electron gas, Quasi-particles, Electron density parameter, Thermal expansion, Thermal conductivity
The understanding of the effect of the interactions between electrons on the metallic state which is based on the Landau's Fermi-liquid theory provides the basis for understanding metals in terms of weakly interacting quasi-particles. At zero temperature a Fermi liquid has a Fermi surface, similar to the non-interacting Fermions [1]. The low lying excitations of the Fermi liquid are called quasi-particles (or Landau quasi-particles). Landau quasi-particles consist of electrons, surrounded by a cloud of spin and charge polarization. They share the same quantum numbers as free electrons but their masses can be strongly renormalized by the back flow of the surrounding fluid [2]. When materials undergo Thermodynamical change, the energy received is in form of heat hence, its temperature rises and thereby changes in dimension [3]. Heat capacities, thermal expansion, thermal conductivities are few important properties often critical in the practical and engineering applications of solids. Nodar, and Levan, [4] generalized the Landau’s theory of Fermi liquids by incorporating the de Broglie waves diffraction. A newly derived kinetic equation of the Fermi particles is used to derive a general dispersion relation and the excitation of zero sound is studied. A new mode is found due to the quantum correction. It is shown that the zero sound can exist even in an ideal Fermi gas. They also disclose a new branch of frequency spectrum due to the weak interaction. Sykes and Brooker [5] derived exact expressions for the transport properties of a degenerate Fermi liquid. The coefficients of shear viscosity, thermal conductivity, diffusion and second viscosity were evaluated giving solution for shear viscosity, and diffusion that agree within 25% with those originally quoted. However, the thermal conductivity is reduced by a factor of about 2. The coefficient of second viscosity was shown to vary with temperature like T2. Gangadharaiah, et al. [6] consider a system of 2D fermions with a short-range interaction. A straight forward perturbation theory is shown to be ill defined even for an infinitesimally weak interaction, as the perturbative series for the self-energy diverges near the mass shell. They show that the divergences result from the interaction of fermions with the zero-sound collective mode. By re-summing the most divergent diagrams, they obtain a closed form of the self-energy near the mass shell. The spectral function exhibits a threshold feature at the onset of the emission of the zero-sound waves. They also show that the interaction with t he zero sound does not affect a non-analytic, part of the specific heat. In this work, we modified the Fermi liquid theory using the electron density parameter and the modified Fermi liquid theory is used to compute the thermal expansion and thermal conductivity of Fermi liquid in other to see the predictability of our modified Fermi liquid theory.
Thermal Expansion of Quasi-Particles
The delocalized free-electron gas of a metal also contributes to the thermal expansion of the metal, in addition to the an harmonic atomic vibrational contribution, the pressure of the Fermi gas is given by [7]
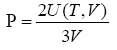 (1)
(1)
Where, U (T,V ) is given as, 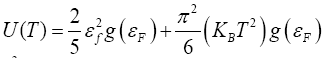 (2)
(2)
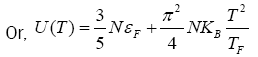 (3)
(3)
Since the volume thermal-expansion coefficient is given by [8],
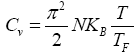 (4)
(4)
Where B is the bulk modulus, there is a positive electronic contribution to the thermal expansion because U (T,V) is an increasing function of T. The thermal-expansion coefficient is given as,
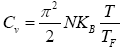 (5)
(5)
Eqn. (5) can be written by using,
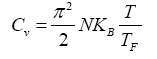 (6)
(6)
and also the Bulk modulus equation given by,
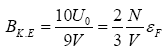 (7)
(7)
In atomic units the bulk modulus of metals is given by,
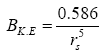 (8)
(8)
and. 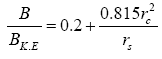 (9)
(9)
Hence, 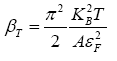 (10)
(10)
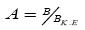 a temperature independent constant,
a temperature independent constant, 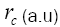 is the Ashcroft core radius and rs is the electron density which
varies between 2 and 6 for most metals. Recall that the Fermi energy of the metals at the Fermi surface is given by [9],
is the Ashcroft core radius and rs is the electron density which
varies between 2 and 6 for most metals. Recall that the Fermi energy of the metals at the Fermi surface is given by [9],
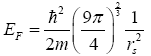 (11)
(11)
Inserting eqn. (11) into eqn. (10), then, the thermal expansion of quasi-particles in terms of the electron density parameter rs is expressed as,
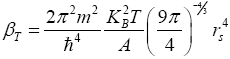
Thermal Conductivity of Quasi-Particles
The Boltzmann transport equation is given by [5],
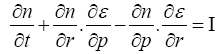 (13)
(13)
Here 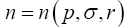 is the distribution function for quasi-particles. The energy
is the distribution function for quasi-particles. The energy 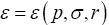 of a given quantum level
depends upon the distribution of the other particles; therefore ε can vary from place to place (even in the absence of an external
field) if the liquid is inhomogeneous.
of a given quantum level
depends upon the distribution of the other particles; therefore ε can vary from place to place (even in the absence of an external
field) if the liquid is inhomogeneous.
The left-hand side of the Boltzmann transport equation is expanded to give,
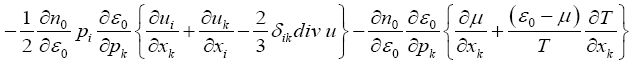
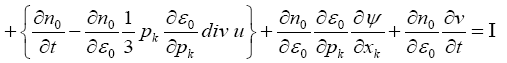 (14)
(14)
The term in the left-hand side of eqn. (14) relevant to the thermal conductivity is given by,
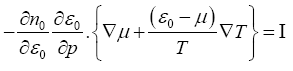 (15)
(15)
Where μ is the Fermi energy? If we approximate 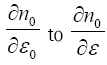 and change
and change 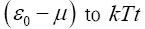 eqn. (15) becomes,
eqn. (15) becomes,
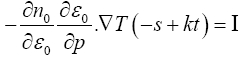 (16)
(16)
where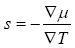 . Here
. Here 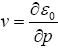 is a function of energy, and is expanded as a power series in t. The direction of the polar axis
is taken to be that of ∇T , which means that the left-hand side contains cosΘ as its only spherical harmonic [6] then we will have,
is a function of energy, and is expanded as a power series in t. The direction of the polar axis
is taken to be that of ∇T , which means that the left-hand side contains cosΘ as its only spherical harmonic [6] then we will have,
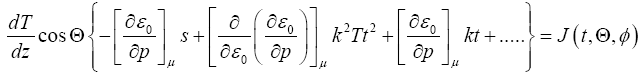 (17)
(17)
Then a solution of the form is applied and is given as,
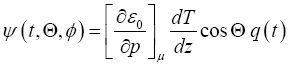 (18)
(18)
The coefficient of q(t) is made a quantity that is evaluated at the Fermi surface, so that all of the variation with energy is defined to be in q (t). Recall that,
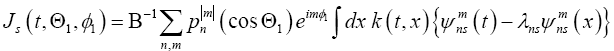 (19)
(19)
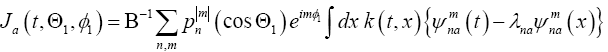 (20)
(20)
Then substituting eqn. (18) into eqns. (19) and (20), we have,
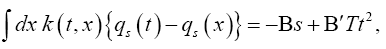 (21)
(21)
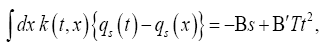 (22)
(22)
 (23)
(23)
and 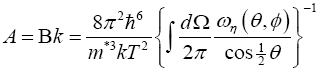 (24)
(24)
Eqns. (21) and (22) are the integral equations that are to be solved in order to find the thermal conductivity. By considering
first eqn. (21) it is shown that 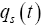 is of the order
is of the order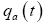 , so that it is negligible beside
, so that it is negligible beside 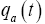 . In addition the argument is fairly lengthy. First we have to evaluate
. In addition the argument is fairly lengthy. First we have to evaluate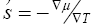 . When a temperature gradient is imposed on the Fermi liquid, the physics of the
liquid determines the gradient of µ , so that it must be possible to find ∇µ from the transport equation. The required condition
is provided by the conservation of momentum, given by,
. When a temperature gradient is imposed on the Fermi liquid, the physics of the
liquid determines the gradient of µ , so that it must be possible to find ∇µ from the transport equation. The required condition
is provided by the conservation of momentum, given by,
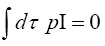 (25)
(25)
Using eqn. (14) we have,
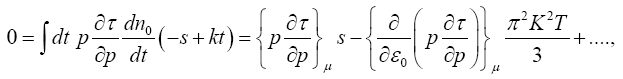 (26)
(26)
S is the entropy per particle and more physically,
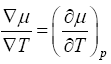 (27)
(27)
From eqn. (27) it appears that in the presence of a temperature gradient the liquid arranges itself to be at a uniform pressure [5]. Recall that,
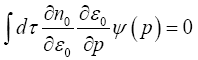 (28)
(28)
Eqn. (28) can be rewritten as,
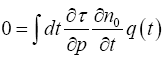
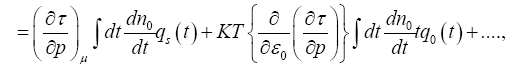
Considering eqn. (14), the solution consists of a particular solution and a complementary function which is zero. The thermal conductivity k is given by,
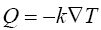 (30)
(30)
Where Q is the flux energy, given by,
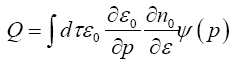 (31)
(31)
Then from eqn. (18)
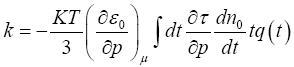 (32)
(32)
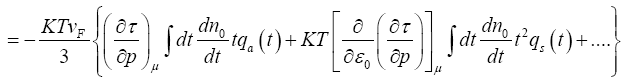
We can see that the contribution of qs to the thermal conductivity is two factors of T smaller than that of qa , so the even function need be considered no further. The odd function is taken into consideration, and using eqn. (32) and
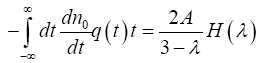
Then we have, 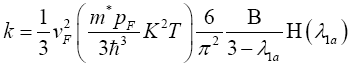
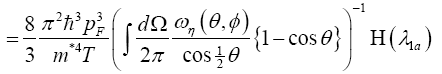
where, 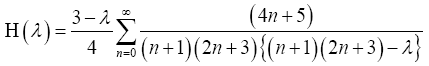
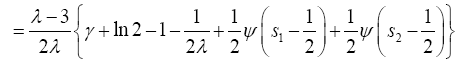
and 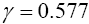 while s1 and s2 are given as,
while s1 and s2 are given as,
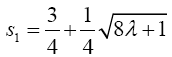 and
and 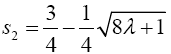 (36)
(36)
Recall that the Fermi momentum of the quasi-particles at the Fermi level is given as [9],
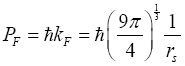 (37)
(37)
Inserting eqn. (37) into eqn. (34), then, the obtained thermal conductivity of quasi-particle in terms of the electron density parameter rs is,
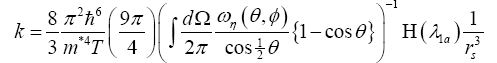 (38)
(38)
Figures 1 and 2 show the relationship between the computed thermal expansion of quasi-particles and Landau thermal expansion of quasi-particles with temperature for some metals respectively. The results revealed that the thermal expansion of quasi-particles increases as temperature increases for all the metals investigated. Also, the computed thermal expansion of quasi-particles in metals is larger than the Landau thermal expansion of quasi-particles in metals. This may be as a result of the electron density parameter used to modify the Landau Fermi liquid theory and some approximations made. In both cases as temperature increases the thermal expansion of quasi-particles is closer to the bulk thermal expansion. But the computed thermal expansion of quasi-particles is closer to bulk thermal expansion of metals than the Landau thermal expansion of quasiparticles. This suggests that as temperature increases the amplitude of the lattice vibration of quasi-particles increases, the average interatomic distance becomes greater than the zero-temperature separation and hence thermal expansion is enhanced [7]. In all the metals investigated transition metals have lower thermal expansion than alkali and alkali earth metals. This is due to high concentration of quasi-particles in transition metals.
Figures 3 and 4 show the relationship between the computed thermal conductivity of quasi-particles and Landau thermal conductivity of quasi-particles with temperature for some metals. The result revealed that for all the metals investigated the thermal conductivity of quasi-particles decreases as temperature increases. This seems to suggest that as temperature increases the separation between quasi-particles increases because they are not heavy particles hence, the rate of absorbing heat decreases. It is also observed that the computed thermal conductivity of quasi-particles for monovalent metals is larger in transitions metals (copper (Cu), silver (Ag) and gold (Au)) than most of the alkali metals. This is due to the d-block electrons that have filled electron shell which lies high up in the conduction band in noble metals [10]. This shows that thermal conductivity of quasi-particles depends largely on the electron concentration of metals. The experimental thermal conductivity of metals is higher than the computed thermal conductivity of quasi-particles and the computed thermal conductivity of quasi-particles is higher than the Landau thermal conductivity of quasi-particles. But the value of the computed thermal conductivity of quasi-particles is closer to the value of the experimental thermal conductivity of metals. This seems to suggest that the modified Landau Fermi liquid theory can account and predict very well the contribution of quasi-particles to the thermal conductivity of metals.
The thermal expansion of quasi-particles increases as temperature increases for all the metals investigated. In both cases as temperature increases the thermal expansion of quasi-particles is closer to the bulk thermal expansion. But the computed thermal expansion of quasi-particles is closer to bulk thermal expansion of metals than the Landau thermal expansion of quasiparticles. Also, it is observed that the experimental thermal conductivity of metals is higher than the computed thermal conductivity of quasi-particles and the computed thermal conductivity of quasi-particles is higher than the Landau thermal conductivity of quasi-particles. But the value of the computed thermal conductivity of quasi-particles is closer to the value of the experimental thermal conductivity of metals. This seems to suggest that the modified Landau Fermi liquid theory can account and predict very well the contribution of quasi-particles to the bulk thermal expansion and thermal conductivity of metals. In both properties the Landau theory of Fermi liquid under estimated the contribution of quasi-particles to bulk metals.