1Department of Mathematics, Islamabad Model College For Boys, Islamabad, Pakistan
2Department Of Mathematics and Statistics, Riphah International University, Islamabad, Pakistan
Received date: 09/01/2018 Accepted date: 10/05/2018 Published date: 11/06/2018
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In this paper we discuss the representations of a full transformation semigroup over a finite field. Furthermore, we observe some properties of irreducibility representation of a full transformation semigroup and discuss the linear representation of a zero-adjoined full transformation semigroup. Moreover, we characterize the linear representation of a full transformation semigroup over a finite field Fq (where q is a prime power) in terms of Maschke’s Theorem. Finally, we observe that there exists an isomorphism between the full matrix algebra (Fq)m and the space of all linear transformation L(Fq m) on an m-dimensional vector space Fq m
Semigroup of transformations; Representation of semigroup; Finite field
Serre has given a comprehensive theory of linear representation of finite groups in [1]. It has been obtained in the group theory that the number of simple FG− modules is equal to the number of conjugacy classes of the group G such that the characteristic of the field F does not divide the order of G. A lot of work is done for the classification of groups in terms of its representation and characterization.
By Clifford, each element of a semigroup is uniquely determined by a matrix over a field and a complete classification of the representations of a particular class of a semigroups is given in [2-4]. Moreover, irreducible representations of a semigroup over a field is obtained as the basic extensions to the semigroup of the extendible irreducible representations of a group, and the representations of completely simple semigroup is also constructed in [2-4].
Stoll has given a characterization of a transitive representation, and obtained a transitive representation of a finite simple semigroup, see [5]. The construction of all representations of a type of finite semigroup which is sum of a set of isomorphic groups is also obtained. Munn obtained a complete set of inequivalent representations of a semigroup S which are irreducible in terms of those of its basic groups of its principal factors. He also introduced the principal representations of a semigroup in [6]. A representation of semigroup whose algebra is semisimple is characterized in [7,8]. The representation of a finite semigroup for which the corresponding semigroup algebra is semisimple is also obtained. An explicit determination of all the irreducible representations of Tn is due to Hewit and Zuckerman in [9].
There is a one-to-one correspondence between the representations of a group G and the nonsingular representations of the semigroup S, which preserves equivalence, reduction and decomposition [10].
In the case of an irreducible representation of a finite semigroup, the factorization can be avoided and an explicit expression of such representation is given in [11]. We consider a full transformation semigroup Tn to obtain its combinatorial property with regard to its irreducible representations. There exists a non-zero linear transformation satisfying some specific conditions in Theorem 7.3.
It is observed that for the basis  of a vector space
of a vector space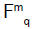 , there is a natural one-to-one correspondence (between the resentations of a full transformation semigroup
, there is a natural one-to-one correspondence (between the resentations of a full transformation semigroup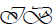 over a finite field Fq and those of the algebra Fq[
over a finite field Fq and those of the algebra Fq[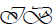 ] which preserves,
equivalence, reduction and decomposition into irreducible constituents.
] which preserves,
equivalence, reduction and decomposition into irreducible constituents.
Consequently, we reinterpret the Maskhe Theorem [12] regarding the algebra Fq[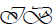 ] i.e., the algebra Fq[
] i.e., the algebra Fq[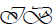 ] is semisimple
if and only if the characteristic of Fq does not divide the order mm of the full transformation semigroup
] is semisimple
if and only if the characteristic of Fq does not divide the order mm of the full transformation semigroup 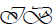 .
.
The representation of full trasformation semigroup over a finite field is discussed in Section-8, specially the Maschke’s
theorem is restated for the semisimplicity of the semigroup algebra Fq[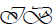 ], see Theorem 8.1 Finally, a linear algebraic result
regarding the isomorphism between the full matrix algebra (Fq)m and the space of all the linear transformations on Fqm is given in
Theorem 8.2.
], see Theorem 8.1 Finally, a linear algebraic result
regarding the isomorphism between the full matrix algebra (Fq)m and the space of all the linear transformations on Fqm is given in
Theorem 8.2.
Definition
A transformation semigroup is a collection of maps of a set into itself which is closed under the operation of composition of functions. If it includes identity mapping, then it is a monoid. It is called a transformation monoid.
If (X,S) is a transformation semigroup then X can be made into semigroup action of S by evaluation, x.s=xs=y for s  S, and
x,y
S, and
x,y  X. This is the monoid action of S on X, if S is a transformation monoid.
X. This is the monoid action of S on X, if S is a transformation monoid.
Hewitt and Zuckerman gives a treatment of the irreducible representation of the transformation semigroup on a set of finite cardinality [8]. The result for the case of a finite semigroup S with F[S] semisimple was given by Munn in [13].
The full reducibility and the proper extensions of irreducible representations of a group to those of a semigroup are the basic extensions.
THEOREM 2.2
Full reducibility holds for the representations of a semigroup S over the field F if and only if
Full reducibility holds for the extendible representations of G over F, and
The only proper extension of a proper representation of G to S is the basic extension [14].
A representation M of S is homomorphism of S into the multiplicative semigroup of all (α,α) matrices( where α is an arbitrary
positive integer) such that M(x) ≠ 0 for some x  S. If the set {M(x): x
S. If the set {M(x): x  S} is irreducible i.e., if every (α,α) matrix is a linear combination
of matrices M(x), then M is said to be an irreducible representation of S. The identity representation is the mapping that
carries every x
S} is irreducible i.e., if every (α,α) matrix is a linear combination
of matrices M(x), then M is said to be an irreducible representation of S. The identity representation is the mapping that
carries every x  S into the identity matrix.
S into the identity matrix.
Full transformation semigroup
The idea of studying Tn was suggested by Miller (in oral communication). The problem of obtaining representations of semigroup as distinct from groups have been first studied by Suskevic. Clifford has given a construction of all representations of a class of semigroups closely connected with Tn. Ponizovski has pointed out some simple properties of Tn . In the present discussion, we relate the irreducible representations of Tn to that of its semigroup algebra L(Tn). The set of all transformations of set X into itself is called the full transformation semigroup under the binary operation of multiplication as the composition of transformation analogue of the symmetric group GX. Let Xn = {1,2,3,….,n} be a finite set and denote the semigroup TXn of all the self-maps of Xn into Xn. If cardinality of Xn is n, denote Tn for TXn then the cardinality of Tn is nn [15].
Example
The set S={e,a,x,y} is a semigroup under the multiplication. The Cayley’s multiplication table of S is given as follows [16].

If the mapping 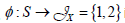 is given by
is given by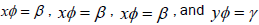 then ф embeds S in
then ф embeds S in 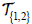 . It can also
be seen that the map
. It can also
be seen that the map 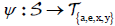 is defined by
is defined by
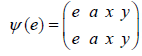
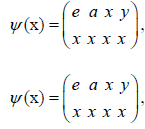
and
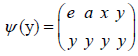
embeds S into 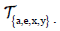
Notice that y is a right regular representation of S, where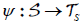 as defined above (where ψ(e), ψ(a), ψ(x), ψ(y)
as defined above (where ψ(e), ψ(a), ψ(x), ψ(y)  TS) is such that for any s
TS) is such that for any s S, we have
S, we have
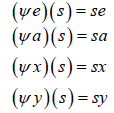
So ψ is a right regular representation of S.
Regular representation of a transformation semigroup
Let K denote the set of right zero elements of a semigroup S. Then, 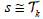 if and only if
if and only if
(i) for all x in K, and all a,b in S, xa=xb implies a=b;
(ii) if α is any transformation of K, then there exists a in S such that xα = xa for all x  K.
K.
An element α of TX is idempotent if and only if it is the identity mapping when restricted to Xα. Suppose that X is a set of
cardinality n. Then, the full transformation semigroup TX contains the symmetric group GX of degree n. 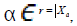 then the rank r
of α is defined by
then the rank r
of α is defined by 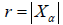 . and the defect of the element a is given by n-r. If b is an element of TX of rank r<n, then there exists
elements γ and δ of TX such that g has the rank r+1, δ has the rank n-1, and β =γδ (we can choose δ as an idempotent, and γ
different from β at only one part of X). By induction, every element of TX of defect k(1 ≤ k ≤ n-1) can be expressed as the product
of an element of GX and k number of(idempotent) elements of defect 1, see also [17].
. and the defect of the element a is given by n-r. If b is an element of TX of rank r<n, then there exists
elements γ and δ of TX such that g has the rank r+1, δ has the rank n-1, and β =γδ (we can choose δ as an idempotent, and γ
different from β at only one part of X). By induction, every element of TX of defect k(1 ≤ k ≤ n-1) can be expressed as the product
of an element of GX and k number of(idempotent) elements of defect 1, see also [17].
If α  TX is of defect 1, then every other element of TS of defect 1 can be expressed in the form λαμ with λ and μ are in GX.
If α is an element of TS of defect 1, then <GXα>= TS .
TX is of defect 1, then every other element of TS of defect 1 can be expressed in the form λαμ with λ and μ are in GX.
If α is an element of TS of defect 1, then <GXα>= TS .
Let X=S be a semigroup, an element ρ  TS is said to be a right translation of S if x(yρ) = (xy)ρ for all x,y
TS is said to be a right translation of S if x(yρ) = (xy)ρ for all x,y  S and λ
S and λ  TX
is said to be a left translation of S if (xλ)y = (xy)λ for any x,y
TX
is said to be a left translation of S if (xλ)y = (xy)λ for any x,y  S. The left and a right translations λ and ρ, respectively, are called
linked if x(yl) = (xr)y for all x;y 2 S.
S. The left and a right translations λ and ρ, respectively, are called
linked if x(yl) = (xr)y for all x;y 2 S.
Note that λaλ = λaλ and ρaρ = ρaρ, if λ and ρ are linked, then

Let S = {e,f,g,α} be a semigroup with the operation “.” given by the Cayley’s table

Cayley’s table
The transformation
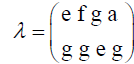
is a left translation which is not linked with any right translations of S. We recall the following proposition regarding the semisimple algebra.
An algebra A is a semisimple if and only if A-module of A is semisimple.
Definition
Let S be a semisimple with zero element z. The contracted algebra F0[S] of S over F is an algebra over F containing a basis  such that
such that  U0 is a subsemigroup of F0[S] isomorphic with S. A semisimple algebra can also be regarded as a contracted semigroup algebra.
U0 is a subsemigroup of F0[S] isomorphic with S. A semisimple algebra can also be regarded as a contracted semigroup algebra.
We recall the following facts regarding the representations of a semisimple algebra.
Lemma
(a) Let 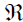 be an algebra having finite order over the field F, and let
be an algebra having finite order over the field F, and let 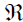 be a radical of
be a radical of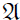 . Then, every non-null irreducible
representation of
. Then, every non-null irreducible
representation of 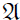 maps
maps 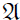 into 0, and so it is effectively a representation of the semisimple algebra
into 0, and so it is effectively a representation of the semisimple algebra 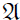 /
/ 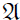 .
.
(b) Let ф be any faithful representation of a semisimple algebra 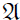 and let P be an n*n matrix over τ Then, P is nonsingular
if and only if ф(n)(P) is non-singular [18].
and let P be an n*n matrix over τ Then, P is nonsingular
if and only if ф(n)(P) is non-singular [18].
THEOREM 4.4
(6, Th. 5.7). An irreducible algebra of linear transformations is simple.
If A  (F)n, then the transformation x → Ax of a vector space V is linear transformation τ of V to V, and the mapping A → A
is an isomorphism of (F)n upon the algebra L[TV] of all linear transformations of V. A homomorphism ф of
(F)n, then the transformation x → Ax of a vector space V is linear transformation τ of V to V, and the mapping A → A
is an isomorphism of (F)n upon the algebra L[TV] of all linear transformations of V. A homomorphism ф of 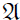 into (F)n is called a
representation of
into (F)n is called a
representation of 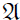 of degree n over F. In other words, to each element x of
of degree n over F. In other words, to each element x of 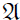 there corresponds an n*n matrix ф(x) such that
there corresponds an n*n matrix ф(x) such that
ф(x+y) = ф(x)+ф(y);
ф(xy) = ф(x)ф(y);
ф(αx) = αф(x):
for all x,y in TN and α in F.
The irreducible representations of semigroups
Let f be an element of TN . Then, f splits the set {1,2,..,n} into a number p of nonvoid disjoint subsets, each of the form {x:f(x)=a}
for some a  rang( f). Obviously, f is determined by these sets and the corresponding a's. For nonvoid subset s of {1,2,…,n}, let
s* be the least element of s. Write the sets {x: f(x)=a} in the order s1,s2,..,sp where s*1<s*2<…< s* p, and represent f by the symbol
rang( f). Obviously, f is determined by these sets and the corresponding a's. For nonvoid subset s of {1,2,…,n}, let
s* be the least element of s. Write the sets {x: f(x)=a} in the order s1,s2,..,sp where s*1<s*2<…< s* p, and represent f by the symbol
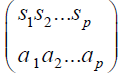
where 1 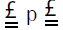 n, the class of sets s1,…,sp is a decomposition of {1,2,..,n} of the kind described above, and a1,a2,…,ap are any distinct integers lying between 1 and n. The expression s1,..,sp will always mean a decomposition of {1,2,..,n} into nonvoid, disjoint subsets with s*1<s*2<…< s* p. The letters t and w will be used similarly. Also a1,a2,...,ap will always mean any ordered sequence of
distinct integers from 1 to n; the letters c and d will be used similarly.
n, the class of sets s1,…,sp is a decomposition of {1,2,..,n} of the kind described above, and a1,a2,…,ap are any distinct integers lying between 1 and n. The expression s1,..,sp will always mean a decomposition of {1,2,..,n} into nonvoid, disjoint subsets with s*1<s*2<…< s* p. The letters t and w will be used similarly. Also a1,a2,...,ap will always mean any ordered sequence of
distinct integers from 1 to n; the letters c and d will be used similarly.
For p = 1,2,…,n, let  p be the set of all elements of
p be the set of all elements of  N whose range contains just p elements, that is,
N whose range contains just p elements, that is,
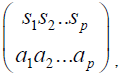
for a fixed p. Strictly speaking,  N depends upon n as well as p. However, only one value of n will be treated at one time. The set
N depends upon n as well as p. However, only one value of n will be treated at one time. The set  N is obviously the symmetric group Sn. The set
N is obviously the symmetric group Sn. The set  p 1 is a semigroup with the trivial multiplication fg=f. No other
p 1 is a semigroup with the trivial multiplication fg=f. No other  p is a subsemigroup of
p is a subsemigroup of  p. It will be convenient to have the semigroup
p. It will be convenient to have the semigroup  p U{z}, with multiplication defined by
p U{z}, with multiplication defined by
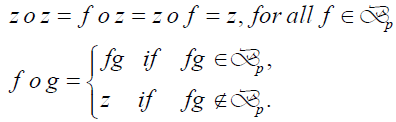
Using a linear algebraic result, we have the following formula regarding the rank of a linear representation of Tn .
THEOREM 5.1
Let M be an irreducible linear representation of Tn , and let S={f:  f Tn and M( f)=0}, then rank[M( Tn )]
f Tn and M( f)=0}, then rank[M( Tn )]

Proof
Suppose the irreducible linear representation M: Tn → L(Tn) is as given above. Since M is irreducible representation of Tn . Thus, using a result in, the set S is void or 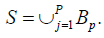
Since,
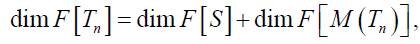
where F is a field of characteristic 0.
Since,
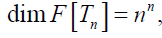
and,
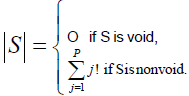
We have
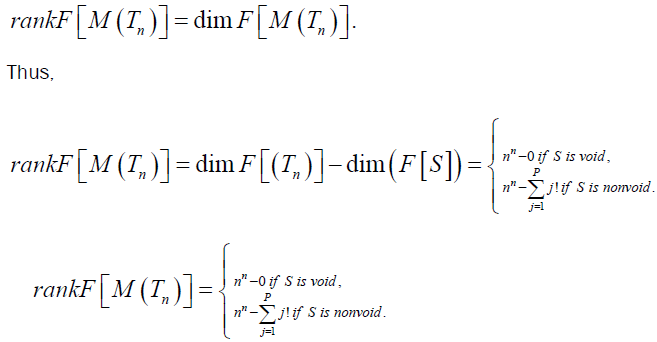
Therefore,
This completes the proof.
Let X={x1,x2,…,xn} be a set of cardinality n and let Sn denote the set of all single-valued maps of X to itself. We have the following characterization of a map from Sn into the set of all n*n matrices Dn over the field F, see also.
THEOREM 5.2
Let M:Sn →Dn be a map defined by M(f) = Af  Dn, for f
Dn, for f  Sn. Then, M forms a homomorphism of Sn into Dn. If, in particular, Sn is a semigroup S, then M becomes a representation of S ∪{z}
into Dn (where z is a zero element).
Sn. Then, M forms a homomorphism of Sn into Dn. If, in particular, Sn is a semigroup S, then M becomes a representation of S ∪{z}
into Dn (where z is a zero element).
Proof
For any two single valued maps f and g in Sn, the product fg is also a single valued map, therefore fg  Sn.
Sn.
Moreover, since  In particular, if i is the identity map on X, then
In particular, if i is the identity map on X, then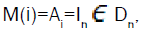 then we have;
then we have;
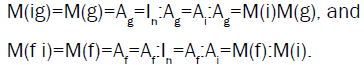
Therefore, M defines a homomorphism of Sn into Dn.
If, in particular, if 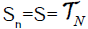 the semigroup of all maps from X into itself, then we can define an induced structure on the adjoined zero semigroup Tn , where z is a zero element, i.e., for any f Tn , we have
the semigroup of all maps from X into itself, then we can define an induced structure on the adjoined zero semigroup Tn , where z is a zero element, i.e., for any f Tn , we have 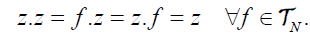
The induced structure on 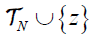 is defined as follows:
is defined as follows:
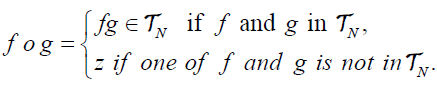
Then, the homomorphism M can be extended into a map 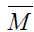 of the semigroup
of the semigroup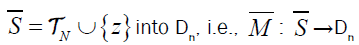 is
defined by
is
defined by
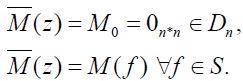
Therefore,
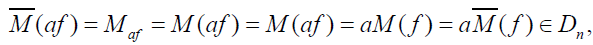
And
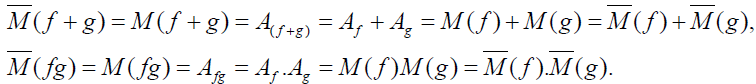
Thus, 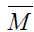 becomes a representation on S.
becomes a representation on S.
Representation of a semigroup of linear transformations in green’s
Relations
Two things that can be associated with an element α 
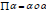 are as follows:
are as follows:
1. the range Xα of α, and
2. the partition 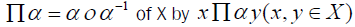 if xα=yα which defines an equivalence relation on X.
if xα=yα which defines an equivalence relation on X.
Let 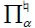 be the natural mapping of X upon the set
be the natural mapping of X upon the set 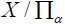 of equivalence classes of X mod
of equivalence classes of X mod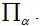 Then,
Then,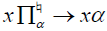 becomes
a one-to-one mapping of
becomes
a one-to-one mapping of 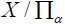 upon Xα. It follows that
upon Xα. It follows that 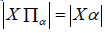 , and this cardinal number is called the rank of α.
, and this cardinal number is called the rank of α.
Remark
The Ex.2.2.6 in [4] can be rewritten as follows,
Let F be a field and V be a vector space over F. By the dimension dimV of we mean the cardinal number of a basis of V over
F. Let 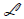 (V ) be the multiplicative semigroup (i.e., under the operation of composition of maps) of all linear transformations of V
with each element t of L(V) we associate two subspaces of V that are given as follows:
(V ) be the multiplicative semigroup (i.e., under the operation of composition of maps) of all linear transformations of V
with each element t of L(V) we associate two subspaces of V that are given as follows:
1. the range 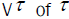 , consisting of all (x) τ with x
, consisting of all (x) τ with x  V and,
V and,
2. the null space Nτ of τ , consisting of all y in V such that (y)τ = 0.
(a) Let 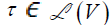 , and W be a subspace of V, complementary to the null space Nτ , so that V = τ
, and W be a subspace of V, complementary to the null space Nτ , so that V = τ
Then, τ induces a non-singular matrix A.
Hence, dim(V=Nτ )=dim(W)=dim(Vt); is called rank of t. The difference or quotient space of V modulo Nτ is denoted by V-Nτ or by V/N 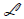 (Tv) . If dimV is finite, this notation of rank is the usual one as for the matrix A, since VA is the row-space of A. Also NA is the orthogonal complement of the column-space of A.
(Tv) . If dimV is finite, this notation of rank is the usual one as for the matrix A, since VA is the row-space of A. Also NA is the orthogonal complement of the column-space of A.
(b) Two elements of the space 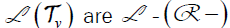 equivalent if and only if they have the same range (null-space). (c) If N and W are subspaces of V such that dim(V/Nτ )=dimW, then there exists at least one element ρ of 1τ such that
N = Nρ and W =Vρ.
equivalent if and only if they have the same range (null-space). (c) If N and W are subspaces of V such that dim(V/Nτ )=dimW, then there exists at least one element ρ of 1τ such that
N = Nρ and W =Vρ.
(d) Two elements 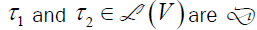 equivalent if and only if rank
equivalent if and only if rank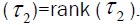
(e) The Th. 2.9 holds for 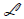 (v) instead of TX if we replace “subset Y of X” by “the subspace W of V”, Tv by dim W, “partition Tv of X” by “subspace N of V ”, and X /Π by dim(V/N).
(v) instead of TX if we replace “subset Y of X” by “the subspace W of V”, Tv by dim W, “partition Tv of X” by “subspace N of V ”, and X /Π by dim(V/N).
Linear representation of a full transformation semigroup over a finite field
Definition
Let V be a vector space over the field F(=C) the complex numbers and let the finite subset 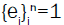 of V be a basis for V, i.e.,
dimV=n, let Tv denote the full transformation semigroup over V. The space
of V be a basis for V, i.e.,
dimV=n, let Tv denote the full transformation semigroup over V. The space 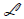 (Tv) denotes the space of all linear transformations
on V. If a is in
(Tv) denotes the space of all linear transformations
on V. If a is in 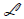 (Tv) a linear transformations, then, each a:V→V is represented by a square matrix (aij) of order n. The coefficients
aij are complex numbers for all i and j=1,…,n and are obtained by
(Tv) a linear transformations, then, each a:V→V is represented by a square matrix (aij) of order n. The coefficients
aij are complex numbers for all i and j=1,…,n and are obtained by
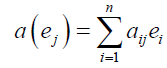
where a can be identified as a morphism which is equivalent to saying that det(a)=det(aij) ≠ 0. The linear space  (Ts) of
full transformation semigroup can be identified with the semigroup of all transformations of degree n.
(Ts) of
full transformation semigroup can be identified with the semigroup of all transformations of degree n.
A representation ф : S →  (Ts) is faithfull if and only if ф is one-to-one homomorphism. A representation ф of a semigroup
S, of degree n over the field F, we mean a homomorphism of S into the semigroup
(Ts) is faithfull if and only if ф is one-to-one homomorphism. A representation ф of a semigroup
S, of degree n over the field F, we mean a homomorphism of S into the semigroup  (TFn) of all linear transformation over Fn,
where
(TFn) of all linear transformation over Fn,
where 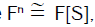 the vector space is generated by S over the field F. Thus, to each element s of S there corresponds a linear transformation
the vector space is generated by S over the field F. Thus, to each element s of S there corresponds a linear transformation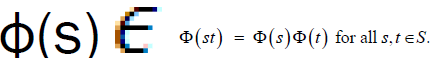 such that
such that
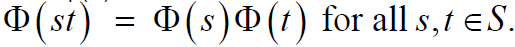
We denote the algebra of all linear transformations over the n-dimensional vector space Fn over the field F by 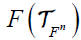 . Obviously,
. Obviously,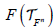 appears as a subspace of
appears as a subspace of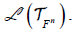
If ф is an isomorphism of S upon a subsemigroup of 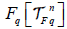 ; then ф is said to be faithfull. We shall determine all the representations
of various classes of finite semigroups over a finite field Fq. If S is a finite semigroup, then there is a one-to-one correspondence
between a representation of S and that of algebra
; then ф is said to be faithfull. We shall determine all the representations
of various classes of finite semigroups over a finite field Fq. If S is a finite semigroup, then there is a one-to-one correspondence
between a representation of S and that of algebra 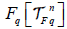 over the finite field Fq. Of course, this correspondence
preserves the reducation, decomposition and hence the full reducibility hold for such representations of S if and only if
over the finite field Fq. Of course, this correspondence
preserves the reducation, decomposition and hence the full reducibility hold for such representations of S if and only if 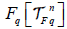 is semisimple that holds if q does not divide the dimFnq=n, (the dimension of the vector space Fnq over a finite field Fq. There is
a necessary and sufficient condition on a finite semigroup S in order that Fq[S] is semisimple. An explicit representation of such
group is obtained in. They constructed all the irreducible representations of S from those of its principal factors of the full transformation
semigroup on a finite set.
is semisimple that holds if q does not divide the dimFnq=n, (the dimension of the vector space Fnq over a finite field Fq. There is
a necessary and sufficient condition on a finite semigroup S in order that Fq[S] is semisimple. An explicit representation of such
group is obtained in. They constructed all the irreducible representations of S from those of its principal factors of the full transformation
semigroup on a finite set.
If F is algebraically closed, then there are no division algebras over F other than F itself, and in this case Wedderbun’s second theorem tells us that every simple algebra ∧ over F is isomorphic with the full transformation semigroup algebra ∧ of degree n for some positive integer n.
Any isomorphism of ∧ upon semigroup ∧ is a representation of ∧ , and gives the irreducible representation of ∧ . Let ∧
be an algebra of order n over F, and let ф be a representation of 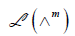 of degree r over F, and let m be a positive integer. For each
element ф(m) of
of degree r over F, and let m be a positive integer. For each
element ф(m) of 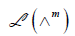 , construct a transformation
, construct a transformation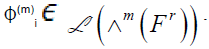
such that
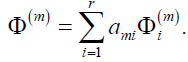

if
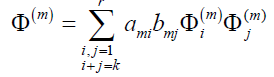
then
The map ф(m) is called the representation of L(Lm) associated with the representation ф of ∧ . The following lemma is due to Van der Waerden’s modern algebra.
Lemma
Let D be division algebra, and let m be a positive integer. The right regular representation ρ of D is an irreducible, and the
only irreducible representation of the simple algebra 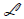 (Dm ) is just the representation ρ(m) of
(Dm ) is just the representation ρ(m) of 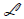 (Dm) associated with ρ.
(Dm) associated with ρ.
THEOREM 7.3
Let ∧ σ (σ=1,…,c) be the simple components of a semisimple algebra ∧ . By Wedderburn’s second theorem, each 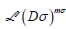 σ may
be regarded as a full transformation
σ may
be regarded as a full transformation 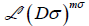 of some degree mσ over the division algebra
of some degree mσ over the division algebra 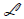 (∧σ ) . Let ρσ be the regular representation
of Dσ and ρσ(mσ) be the representation of
(∧σ ) . Let ρσ be the regular representation
of Dσ and ρσ(mσ) be the representation of 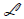 (∧σ ) associated with ρσ then ρσ(mσ) is the only irreducible representation
of ρσ. Extending (ρσ)(mσ) be the representation of
(∧σ ) associated with ρσ then ρσ(mσ) is the only irreducible representation
of ρσ. Extending (ρσ)(mσ) be the representation of 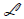 (∧σ ) s sociated with ρσ then ρσ(mσ) is the only irreducible representation of ρσ. Extending (ρσ)(mσ) to
(∧σ ) s sociated with ρσ then ρσ(mσ) is the only irreducible representation of ρσ. Extending (ρσ)(mσ) to 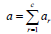 by defining фσ(a) = (ρσ)(mσ)(a) if
by defining фσ(a) = (ρσ)(mσ)(a) if 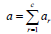 is the unique expression of the element a of ∧ as a sum of
elements ar of the∧r. Then {ф1 ,…,фc} is the complete set of inequivalent irreducible representations of Dσ . If dσ is the order of Dσ , then the degree of фσ is dσ.mσ. If F is algebraically closed, each Ds reduces to F and we may regard L as a direct sum of full
transformation semigroup algebra ∧ over F. The irreducible representation of ∧ are then just the projections of τ upon its various
components (see Th.7.3 in [4]).
is the unique expression of the element a of ∧ as a sum of
elements ar of the∧r. Then {ф1 ,…,фc} is the complete set of inequivalent irreducible representations of Dσ . If dσ is the order of Dσ , then the degree of фσ is dσ.mσ. If F is algebraically closed, each Ds reduces to F and we may regard L as a direct sum of full
transformation semigroup algebra ∧ over F. The irreducible representation of ∧ are then just the projections of τ upon its various
components (see Th.7.3 in [4]).
THEOREM 7.4
Let τ be a linear operator on ∧ with an algebra ∧ of finite order over a field F.
If n > m, then there exists a non-zero linear transformation σ: ∧n →∧m such that τ σ = 0. There exists a non-null transformation γ : ∧n →∧m (over γτ ) such that γτ = 0, for every m > n.
Proof
Let n > m and 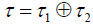 with τ2 an operator on τ2 and τ2 a linear transformation from ∧n−m into ∧n−m (over τ1 ). Suppose that τ1 is left divisor of zero in
with τ2 an operator on τ2 and τ2 a linear transformation from ∧n−m into ∧n−m (over τ1 ). Suppose that τ1 is left divisor of zero in 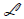 (∧m) . then there exists
(∧m) . then there exists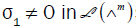 such that τ1 σ1 = 0. We may take σ=(σ1,0). Hence we may
assume that τ1 is not left divisor of zero in
such that τ1 σ1 = 0. We may take σ=(σ1,0). Hence we may
assume that τ1 is not left divisor of zero in 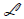 (∧m). By Lemma 5.8, that can be applied to the algebra
(∧m). By Lemma 5.8, that can be applied to the algebra 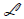 (∧m) ), we have that the algebra τ1 contains a left identity element i with respect to which τ1 has a two-sided inverse ρ1 in τ1
(∧m) ), we have that the algebra τ1 contains a left identity element i with respect to which τ1 has a two-sided inverse ρ1 in τ1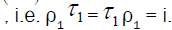 We may
take
We may
take 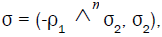 where σ2 is any non-singular linear transformation from ∧m into ∧m over the algebra ∧ .
where σ2 is any non-singular linear transformation from ∧m into ∧m over the algebra ∧ .
Then,
since 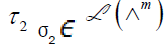 and i is the identity element in
and i is the identity element in 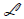 (∧m).
(∧m).
One can similarly prove that, if m > n, then there exists a non-null transformation 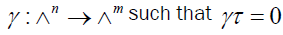
Representation of a full transformation semigroup over a finite field
Let θ be a root of some irreducible polynomial of degree m over a finite field Fq(or the Galois field GF(q)), then the set {1, θ,θ2….,θm-1} becomes a basis for the vector space Fmq over Fq and is called a polynomial basis for Fmq. The dimension of the vector space Fmq over Fq is m. Let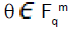 such that the set
such that the set
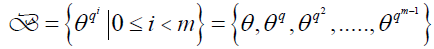
form a basis for 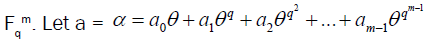 So that a be represented by the vector (a0,a1,a2,…,am-1) and
let αq be represented by the shifted vector (am-1,a0,a1,…,am-2). The normal basis exists for any extension field of Fq.
So that a be represented by the vector (a0,a1,a2,…,am-1) and
let αq be represented by the shifted vector (am-1,a0,a1,…,am-2). The normal basis exists for any extension field of Fq.
Consider the vector space V = Fqm over Fq (where q is a prime), and let  = {θ,θq, θq ….,θqm-1} be a basis for V. Let TB
be the full transformation semigroup upon the basis B. Then T
= {θ,θq, θq ….,θqm-1} be a basis for V. Let TB
be the full transformation semigroup upon the basis B. Then T =mm.
=mm.
Since 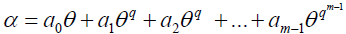 is an element of V =Fqm as described above. Then the element
is an element of V =Fqm as described above. Then the element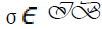 can be defined by
can be defined by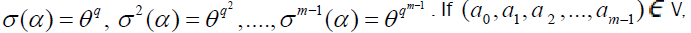 then
then 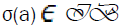 , where
, where
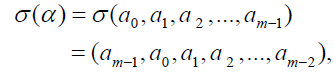
i.e., 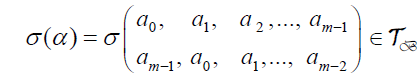
It is obvious to say that . S is a full transformation semigroup over V* with a dual basis
. S is a full transformation semigroup over V* with a dual basis of
V* then there exists a mapping
of
V* then there exists a mapping 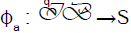 which becomes an isomorphism.
which becomes an isomorphism.
Since is a finite full transformation semigroup on the basis B of V over the finite field Fq. Therefore Fq [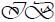 ] becomes
an algebra of
] becomes
an algebra of 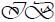 over Fq. Then, there is a natural one-to-one correspondence between the representation of TB over Fq and
those of
over Fq. Then, there is a natural one-to-one correspondence between the representation of TB over Fq and
those of 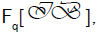 which preserves equivalence, reduction and decomposition into irreducible constituents.
which preserves equivalence, reduction and decomposition into irreducible constituents.
Thus the representations of  over Fq is transferred to the algebra
over Fq is transferred to the algebra  If
If  is semisimple, then by the main representation theorem[4] holds for semisimple algebra
is semisimple, then by the main representation theorem[4] holds for semisimple algebra  Every representation of
Every representation of 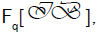 and hence every
representation of TB is full reducible into irreducible one.
and hence every
representation of TB is full reducible into irreducible one.
Let Fq be a finite field, and B be a basis for Fmq , where (m,q) = 1. (i.e., m,q are relatively prime).
Then, we have the following interpretation of the Maschke’s theorem regarding the algebra 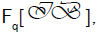 over the finite field Fq.
over the finite field Fq.
THEOREM 8.1
Let Let S =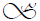 be a finite full transformation semigroup over basis
be a finite full transformation semigroup over basis 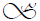 of
of 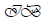 of order mm.
of order mm.
Then, the semigroup algebra 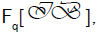 over Fq is semisimple if and only if the characteristic q of Fq does not divides the
order mm of the full transformation semigroup ∧.
over Fq is semisimple if and only if the characteristic q of Fq does not divides the
order mm of the full transformation semigroup ∧.
Let ∧ be an algebra of order r over the vector space V = Fq m, and let n be another positive integer different from m. Denote by ∧ the full matrix algebra of all nn matrices over ∧ , with the additions and multiplication of matrices, and of the multiplication of matrix by a scalar in Fqm. Then, the algebra ∧ is of order rn2 over Fq m. In particular, (Fqm)n will denote the full matrix algebra of degree n over Fqm.
An algebra L over a field F is called division algebra if ∧ /0is a group under multiplication. A result regarding the existence of an isomorphism between a full matrix algebra and the space of all the linear transformations over the vector space Fqm , is as follows.
THEOREM 8.2
Let Fqm be a vector space over a finite field Fq. Then, there is an isomorphism from the space of full matrix algebra (Fq)m to the
space 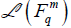 of all the linear transformations on Fqm.
of all the linear transformations on Fqm.
Proof
The set of all m−dimensional vector space (1m matrices) over Fq is an m−dimensional vector space Fqm over Fq . The natural basis of Fqm consists of the m vectors v1 = θ, v2 = θq, v3 =θq2 ,…,vm = θqm-1, where vi has the identity element 1 of Fq for its ith component, and has 0 for the remaining components.
If A  (Fq)m, then the transformation t :
(Fq)m, then the transformation t : 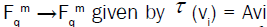 is a linear transformation t of Fqm into itself and the
mapping
is a linear transformation t of Fqm into itself and the
mapping 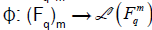 is an isomorphism of
is an isomorphism of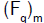 upon the algebra
upon the algebra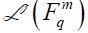 of all linear transformations of Fqm into itself. The ith row of A is the vector
of all linear transformations of Fqm into itself. The ith row of A is the vector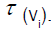
Conversely, if Fqm is any m−dimensional vector space, and we choose a basis {v1,v2,…,vm} of Fqm, then each linear transformation t of Fqm determines a matrix A = (αij) from the expression.
for the m vectors 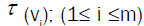 as linear combination of the basis vectors. Then, the mapping
as linear combination of the basis vectors. Then, the mapping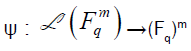 becomes
an isomorphism of
becomes
an isomorphism of 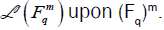
A combinatorial result about the rank of a representation of the full transformation semigroup is obtained. It seems that for any homomorphism between the set of single-valued maps and the set of all nn matrices over a field F becomes a representation when the set of single valued maps is replaced by a full transformation semigroup adjoined with a zero element z. There is a one-one correspondence between the set of all representations of some finite semigroup S and those of the algebra of a full transformation semigroup over a finite dimensional vector space over a finite field. Consequently, we observed an isomorphism between the full matrix algebra (Fq)m and the set of all linear transformations on Fqm is obtained.