Research & Reviews: Journal of Pure and Applied Physics
MenuISSN: 2320-2459
ISSN: 2320-2459
Department of Physics, Beinstein College of Science, Jalukbari, Guwahati, Assam, India
Received Date: 24/03/2017; Accepted Date: 31/08/2017; Published Date: 06/09/2017
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Due to immature cells, low blood flow rate, high density and lack of oxygen environment inside the tumour, it is experimentally seen that, tumour cells at temperature between 42°C and 46°C the viability of the cancerous cells is reduced 5,14. Therefore efficiency of chemotherapy and radiation is increased. In recent years due to the development in area of nano technology, magnetic nanoparticle (MNPs) hyperthermia has been deeply studied as a promising new tumour therapy, because in presence of an alternating magnetic field they show remarkable heating effects. In order to achieve efficient and safe operational hyperthermia conditions, it is necessary to study or investigate detail about what heating model or magnetic loss processes dominant over the other in the ensemble of nanoparticles which are injected at the cancerous tumour site. Because there is more than one heat loss process are involved in generating heat by MNPs. First experimental work on magnetic materials for hyperthermia was carried by Gilchrist in 1957. He heated various tissue samples with the help of different sizes of γ-Fe2O3. Since then, there have been numerous theoretical and experimental work has been done by different people on different nanoparticles. Here, in this work we compare theoretical results given by different MNPs .And taking into account cellular uptake mechanism it is showed that at a low frequency of applied magnetic field maghemite and at a high frequency of applied magnetic field FeCo is the best magnetic particle to use for the hyperthermia.
Magnetic Nanoparticles (MNPs), Nanoparticles (NPs), Relaxation time, Critical size, Blocking temperature
“Those who cannot be cured by medicine can be cured by surgery. Those who cannot be cured by surgery can be cured by heat. Those who cannot be cured by heat are probably incurable” Hippocrates - 470-377 B.C.
Generally, tumour is the cluster of cells undergoing uncontrolled growth of cell in the body. These cancerous cells are more sensitive to temperature in the range 42-46°C compared to healthy cells [1]. Therefore different theoretical and experimental study have been done in last few decades on the field of oncology, to kill cancerous cells by increasing the temperature of the cancer cells. Main problems involved in the traditional tumour or cancer therapy is that this method also damages the healthy tissue with cancer cells. And also in this process the use of powerful toxic drugs results in an unwanted side effect in our body. Development in nano technology has provided magnetic nanoparticles hyperthermia is one of the most promising approaches in cancer therapy to come out with a solution of above problems by localized heating inside the tumour. Magnetic nanoparticles hyperthermia has negligible side effect compare to other process.
In magnetic nanoparticles hyperthermia, MNPs are injected near the tumour site using a steady magnetic field either applied non-invasively or surgically at the tumour site. Once the MNPs are deposited on site then an alternating magnetic field is applied for maximum 40-50 mins. The energy of this alternating magnetic is absorbed by the magnetic nanoparticles and these particles exited to higher energy level. This excess energy of the particles is dissipating as heat to the surrounding. Since, in tumour low blood flow rate, high density condition is present, therefore this helps localised heating inside the tumour. And healthy tissue will be unaffected by this treatment.
Different mechanism is involved in the heating process of the MNPs in the presence of alternating magnetic field. And also dependency heating powers on the size of the MNPs make the process more interesting and theoretical. First experimental invest igations of the application of magnetic materials for hyperthermia are carried out by Gilchrist in 1957 [2]. He heated various tissue samples different sizes particles of γ-Fe2O3 exposed to a 1.2 MHz magnetic field. After that many other theoretical as well as experimental work have been performed with different MNPs. Here in this novel work we also take into account the cellular uptake mechanism and we theoretically showed that magnetite and FeCo will be the best nanoparticles for hyperthermia process.
MNPs are subjected to an alternating magnetic field to turn them into a heat source. There are three different mechanisms by which magnetic materials can produce heat in presence of an alternating magnetic field. These are
1. Generation of eddy currents in magnetic particles.
2. Hysteresis losses in multi-domain MNPs,
3. Relaxation losses in ‘super paramagnetic’ single-domain MNPs,
But for the case of MNPs, heat produce due to eddy current decrease considerably as the size of the magnetic particles reduced to nanometre range. And also to generate heat by eddy current required high frequency alternating magnetic field. At such a high frequency field eddy current also generated heat in the normal tissue. This causes the serious side to the patients. So in modern magnetic nanoparticle hyperthermia eddy current loss does not take into account.
The hysteresis loop of magnetic materials is characterized mainly by three typical material dependent parameters: Saturation magnetization MS, Remnant magnetization MR and coercively HC. All these parameters are important for the heat output of nanoparticles and may vary considerably for different particle types.
The power dissipated by a per unit mass magnetic material per oscillation subjected to an alternating magnetic field is often called the "Specific Absorption Rate" (SAR)of magnetic hyperthermia. For a field amplitude H it is expressed as 3.
SAR(H)=0; H≤HC
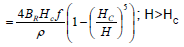
BR is remnant flux density.
One of the most unique things in magnetic nanoparticle is that the value of coercively is strongly dependent on the size of the particles. At first as the size of the particle decrease to nano scale coercively also increase, but at particular size of the nanoparticle coercively achieve the maximum value afterwards it decrease sharply as the size of the particle further decrease. This size dependent coercively value for particle size D can expressed as 3.
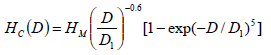
Where, D1 is a constant. Since SAR value is strongly depend on HC, so SAR value also changes with size of the nanoparticles. So for a very fine small particle hysteresis contribution to heat dissipation is very small 12.
Mainly, in nano scale range relaxation loss is alone responsible over the other two mechanisms for heat generation process of MNPs.
Magnetic domains exist in the macroscopic samples of magnetic materials, and they are separated by domain walls. Because
of spin-orbital interactions of the electrons in the NPs produce magnetic anisotropy. For isolated systems, the magnetic anisotropy
is responsible for keeping the spins in a particular direction. Since atomic orbital have non-spherical shapes, therefore they try to
align in a specific direction which is called the easy direction. Energy is required in order to rotate the magnetization away from the
easy direction. This required energy is called the anisotropy energy. In general, the anisotropy energy per particle is expressed by E = KV2 sinθ where K is the anisotropy constant (it includes all sources of anisotropy), V (=r3) is the volume of the particle, and
θ is the angle between the particle magnetization and the easy magnetization axis of the particle 4, 13, 14. The higher order terms
can be neglected. From the above equation, it is seen that the anisotropy energy directly depends on the particle size and on the
anisotropy constant. For a fixed anisotropy constant K, as the size of the particle r decreases, anisotropy energy E also decreases.
At nanoscale size, the particle prefers to have only one magnetic domain and it is called as single-domain NP. At this very small
size, the anisotropy energy become smaller than the thermal energy,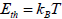 
(kB is the Boltzmann constant). Therefore, in the
absence of an external magnetic field the particle magnetic moment starts to rotate freely in all probable directions leading to zero
net magnetization. While the particle orientation is fixed, if the flipping of magnetic moment start, then the relaxation time of the
moment is called the Neel relaxation time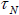 
, and is given by: 2, 13,14.
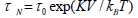
Where,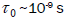 
.
In a fluid medium of viscosity η, additionally a second relaxation mechanism occurs due to rotation of the particles itself is commonly referred to as Brown relaxation with the characteristic relaxation time 2
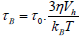
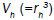is the hydro-dynamically effective volume, which is differ from the geometrical volume. Including the ligand layer
hydrodynamic volume can be written as: 2.
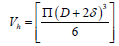
Where D is the diameter of MNP and δ is the ligand layer thickness.
Of course, particles will choose the energetically ‘easiest way’ for reversal of magnetization. This means that reversal will
occur via that process which has the smaller relaxation time. Neel relaxation decreases faster compare to Brown relaxation due
to the exponential dependent of volume of the particle. An effective relaxation time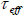 
can be defined by:
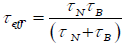
Imagine that the magnetization of a single super paramagnetic nanoparticle is measured in time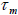 
. If
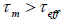, the
nanoparticle magnetization will flip several times during the measurement, then the measured magnetization will average to
zero. If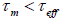 
, the magnetization will not flip during the measurement, so the measured magnetization will be what the
instantaneous magnetization was at the beginning of the measurement. In the former case, the nanoparticle will appear to
be in the super paramagnetic state whereas in the latter case it will appear to be “blocked” in its initial state. The state of
the nanoparticle depends on the measurement time. A transition between super Para magnetism and blocked state occurs
when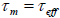 
. In several experiments, the measurement time is kept constant but the temperature is varied, so the transition
between super Para magnetism and blocked state is seen as a function of the temperature. The temperature for which is called
the blocking temperature.
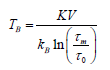
Power dissipation
The internal energy of a magnetic system in an adiabatic process, [3-6]
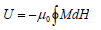
Thus, the power dissipation in unit second due to magnetic field of frequency f, [7]
P =Uf
The volumetric power dissipation of magnetic nanoparticles [8]
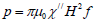
Where μ0 the permeability of is free space and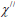 
is the imaginary part of the susceptibility
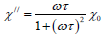
Where
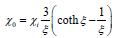
Where ξ and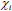 
are the Langevin parameter and initial susceptibility is respectively
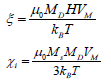
Here, MD and VM are the domain and saturation magnetization, respectively.
From the above equations the heat losses by MNPs in a fluid medium when exposed to an ace field are not only dependent on the amplitude and frequency of the applied magnetic field, but also depend on the physical and magnetic properties of the MNP and the material parameters of the carrier fluid [11-13].
Cellular uptake
Heat dissipation by hyperthermia is a intercellular process. So for efficient hyperthermia high cellular uptake rate of the nanoparticles is very mush necessary. Generally surface of the cell membrane covered with receptors. When particles come close to the receptors they selectively bound the particles. As a result some chemical energy is released, which is equal to Lbε . Where Lb is the number receptors in the membrane that bound the particles and ε is the chemical energy released for each bound receptors. Using this chemical energy receptors pull the nanoparticles towards the inside of the membrane to intercellular compartment [14]. Considering all the mechanism that are effecting the cellular uptake process it is calculated that there is a critical size for which cellular uptake of the particles is maximum, which is equal to 1.
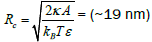
Where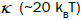 
is the bending modulus of the membrane and A is area of the each receptors. For the nanoparticles
which are smaller than this size cellular uptake negligibly small. And also as the size increase above the critical value cellular
uptake decrease linearly with the size.
Analysis
In hyperthermia we need high heat dissipation loss by the nanoparticles. From the Figure 1 we see that various nanoparticles have maximum heat dissipation for certain size of the particle. Above and below this size heat dissipation value drops down quickly. From this we can conclude that size distribution of the nanoparticle should be very small for efficient hyperthermia treatment. And among the various particles FeCo has high heat dissipation [15].
Figure 1: Profile of power dissipation with variation in size of the magnetic nanoparticle for different nanoparticles.
Different particles with maximum heat dissipation critical size particle are the given below:
| Materials | Qmax (w/m3) | Critical size (nm) |
|---|---|---|
| FePt | 4.5 × 105 | 5 |
| Fe | 7.9 × 105 | 8 |
| FeCo | 8.2 × 105 | 27.5 |
| Fe3O4 | 2.1 × 105 | 13.5 |
| γ-Fe2O3 | 2 × 105 | 19 |
Now using the data for magnetite we plot a profile of heat dissipation with variation in size of the particle for different frequency of the applied ac magnetic field at constant field amplitude (Figure 2) [16].
Figure 2: Profile of power dissipation with variation in size of the magnetic nanoparticle at different Frequency of alternating magnetic field for magnetite.
Similarly using the same equation for magnetite we plot heat dissipation profile with variation in size of the particle for different amplitude of the field at a constant frequency [17,18]. It is observed the figure that as the amplitude of the magnitude field increase heat dissipation also increases sharply. But critical size of the particle does not change with the field unlike the change in the frequency of the ac field (Figure 3).
Figure 3: Profile of power dissipation with variation in size of the magnetite nanoparticle at different amplitude of magnetic field.
From the Figure 2 we have seen that power dissipation increase as increased frequency of the magnetic field. Another point we conclude from the profile is that critical size at which maximum dissipation is obtain is shifted is decrease as we increase the frequency of the field. The profile of variation of critical size with the variation in frequency of the field is shown in the Figure 4.
Figure 4: Profile of critical size at which maximum dissipation occurs with variation in frequency of the applied field as per the Figure 2.
As we already discussed that hyperthermia is efficient only when cellular uptake high. From the cellular uptake mechanism we know that cellular uptake is maximum value at the critical size of the particle 19 nm 1. And from the above figure we see that magnetite has the maximum value of heat dissipation at the critical size 18.8 nm for 100 kHz frequency of applied magnetic field. So from these two points we can conclude that magnetite is an efficient nanoparticle for hyperthermia.
And since cellular uptake has an optimal value for range 19-25 nm-1, hence FeCo also can be used as MNP for hyperthermia for high frequency of applied magnetic field. Because FeCo has a very high heat dissipation values in the range 22-28 nm.
Though FePt and Fe have high heat dissipation but due to their low cellular uptake they are not consider for efficient hyperthermia.
It is an interesting challenge task for future research to increase the biological efficacy and particle specific absorption rate in order to achieve efficient and safest magnetic particle hyperthermia.
I confirm that this work is original and has not been published elsewhere, nor it is currently under consideration for publication elsewhere.
We have no conflicts of interest to disclose.
And it is defined as [