ISSN: 2320-2459
ISSN: 2320-2459
Edusei G1*, Andam AB1, Banini GK1, Fletcher JJ2 and Tandoh J2
1Graduate School of Nuclear and Allied Sciences, University of Ghana P.O. Box AE1, Atomic-Kwabenya, Ghana
2Ghana Atomic Energy Commission (GAEC), P.O. Box LG 80, Legon, Accra, Ghana
Received Date: 27/09/2017; Accepted Date: 11/10/2017; Published Date: 17/10/2017
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
The radio nuclide 67Cu (T1/2=62 h) is an important positron emitter, suitable for combining SPECT imaging and therapy. We evaluated three reactions, namely 68Zn(p,2p)67Cu, 70Zn(p,α)67Cu and 64Ni(α,p)67Cu. Data analysis was generally limited up to about 50 MeV using the nuclear model code TALYS-1.6. The result compared favourably with earlier experimental as well as other theoretical works in literature. Using the radionuclide production yield equation, the calculated thick target yield for 70Zn(p, α)67Cu reaction is 6.3 MBq/μA. The effect of certain operational parameters on the thick target yield of copper-67 was investigated and a numerical equation was obtained for thick target yield by employing standard integral method. A critical comparison of the various production routes of 67Cu is presented. The 70Zn (p, n) 64Cu reaction, utilizing a highly enriched target, is the method of choice if low energy cyclotron are available
64Cu production, Excitation functions, Calculate thick target yields
The radioisotopes 67Cu is a promising and radio metallic isotope for molecular targeted radio pharmaceuticals. Having a half-life of 62 hours and decays100% by emission of β-particles with a maximum energy of 0.6 MeV. The emitted γ-rays are 184.6 keV (48.7%), 93.3 keV (16.1%) and 91.3 keV (7.0%) (NUDAT data base). It is widely used in the form of biomedical substrate – pharmaceutical for single photon emission computer tomography (SPECT) diagnosis and simultaneously for targeted radiotherapy for cancer The most common production method for 67Cu utilizes the 68Zn + p → 67Cu + 2 (or 68Zn (p, 2p) 67Cu) reaction. The target for producing 67Cu is enriched 68Zn (94%). The 68Zn is first prepared and electroplated onto a gold disk. The target is then inserted into a cyclotron for proton bombardment; then the 67Cu is separated from the target zinc or nickel in procedure known as solvent extraction. The enriched nickel and zinc can be recovered and reused for future bombardments because of its high cost [1]. The aim of this paper is to obtain the optimum production yield for the production of 67Cu on an enriched nickel and zinc target over a given range of proton-energy. In this study possible production of 67Cu by 68Zn (p,2p)67Cu, 70Zn(p,α)67Cu and 64Ni(α,p)67Cu were considered. The excitation functions of these reactions reported in the literature are in good agreement with this theoretical excitation function calculated with TALY-1.6 code as shown in Figures 1-3.
Talys Calculations
Taly’s is a computer code system for analysis and prediction of nuclear reaction. The basic objective behind its construction is the simulation of nuclear reactions that involve neutrons, photons, deuterons, tritons, 3He- and alpha-particles, in the 1 KeV- 200 MeV. The most important parameters involving nuclear theory, which were directly used in theoretical calculations of the excitation functions of reactions under consideration over a wide range of energy extending up to 50 MeV. The default optical model potential (OMPs) of TALYs for protons and neutrons are from the local and global parameterization [2] whereas OMPs for deuterons, tritons, helion and alpha particles are based on the folding approach [3]. Depending on the structure of nuclei, calculation for direct reactions can be performed by coupled channel method, the distorted wave born approximation, weakcoupling model for giant resonance description. In all the calculation the default options for the direct reaction were used. The comp ound nucleus was treated within the frame–work of Hauser-Feshbach model along with the width fluctuation correction model of Moldauer, [4] the pre-equilibrium reaction calculation were performed by exciton [5].
Generation of Nuclear Reaction Cross Section
In the estimation of optimum energy range for the production of copper using a cyclotron, cross section of the 68Zn(p,2p)67Cu, 70Zn(p,α)67Cu and 64Ni(α,p)67Cu which are function of their respective particle energies were generated using Taly’s code. This was done by feeding the code with input parameter such as the incident particle, the particle energy, the appropriate target and the atomic mass of the target after which the data is submitted to code to run. After processing, the cross section of the various reaction channels are grouped and displayed into the output of the code.
Using theoretical cross section values, the thick target yields of copper-67 can be calculated using SRIM-2013 for the stopping power. The thick target yield(y) is calculated using Simpson’s numerical integration.
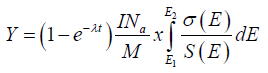 (1)
(1)
Where Na is the Avogadro number, M is the target atomic weight of the target element, σ(E) is the reaction cross section as a function of energy, λ is the decay constant of the product, t is the time of irradiation, I is the projectile current and S(E) is the target stopping power (SRIM, 2013) expressed in unit MeVcm2g-1.
Estimation of Thick Target Radionuclide Production Yield
The thick target radionuclide production yield (Y) is given in eqn. (1) above as well as the expression for cross section σ(E) in equation below
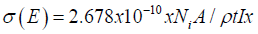 (2)
(2)
And the mathematical equation of stopping power S(E) is given by
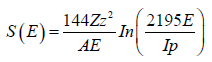 (3)
(3)
Substituting eqns. (2) and (3) into eqn. (1) is
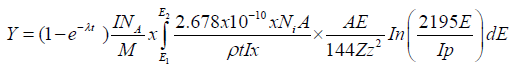 (4)
(4)
Where the limit E1 and E2 represents incident proton energy and exit proton energy respectively
Bringing out and simplifying the constant eqn. (4) becomes
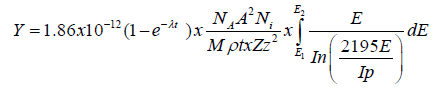 (5)
(5)
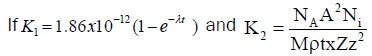
Then eqn. (4) can be written as
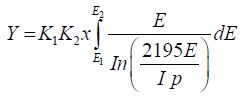 (6)
(6)
Ionization energy (Ip) for Ni→64=7.6398 and for Zn→70=9.3942 (Ionization energies of atoms and ions: Prepared for IAU Symposium 210 (Uppsala Sweden, 2002)
Substituting the values of K1 and K2 into eqn. (5), the production yield equation becomes
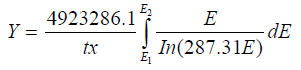 (7)
(7)
Integrating the above equation using standard integral, the final radioisotope production yield equation is written as
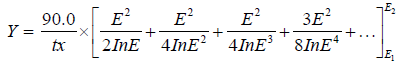 (8)
(8)
Where t is the irradiation time in (hours), x is the thickness in (μm) and E2 and E1 are the energy in and out in (MeV).
Evaluation of Cross Sections of 70Zn (p, α) 67Cu Reaction
Hussain [6] and Tarkanyi [7] performed experimental measurement of nuclear reaction cross section for 70Zn (p, α) 67Cu reaction. This work also focused on the theoretical measurement of nuclear reaction for the same reaction using Talys code. Analysing the figure it could be seen that the excitation function for the three research works increased sharply from 10 MeV and peak art cross section values of 19.4 mb, 13.6 mb and 12.1 mb at 15 MeV respectively. The excitation functions then decreased exponentially until 27 MeV. Where Hussain [6] and Tarkanyi [7] remain fairly constant with an increase in energy. But this work rose sharply again from 33 MeV with increase in cross section and energy.
Evaluation of Cross Sections of 68Zn (p, 2p) 67Cu Reaction
The reaction 68Zn(p, 2p)67Cu which leads to the production of 67Cu were obtained using Taly’s code (2015) and the excitation functions obtained by Hussain [6] and Tarkanyi [7] by experimentally measuring the reaction cross sections for the same reaction. It is observed that the excitation functions of three works rose sharply from 20 MeV. The maximum cross section by this work is 16 mb at 50 MeV and that of Hussain [6] and Tarkanyi [7] are 9.9 mb and 8.2 mb at the same energy. However the reaction cross section measured experimentally is lower than those obtained theoretically by this work within the same energy range as can been seen in the figure below.
Evaluation of Cross Sections of 64Ni (α, p) 67Cu Reaction
An excitation function obtained by this work for 64Ni (α, p) 67Cu and the excitation function obtained by Hussain [6] for the same reaction are shown in the Figure 2 below. It is clear from the figure that the excitation functions of both work raised sharply from 12 MeV until about 19 MeV where there is a deviation of Hussain’s graph at cross section value of (22.9 mb) at 22 MeV, while this work peaks is at a cross section value of (19.8 mb) at 19 MeV. At their maximum peak values for both excitation functions decrease exponentially to about 45 MeV where they remain fairly constant with an increase with proton energy.
Calculation of Thick Target Yields for Copper-67
Analyzing the available theoretical information on the excitation functions for the reaction 68Zn(p,2p)67Cu, 70Zn(p,α)67Cu and 64Ni(α,p)67Cu. These data could now be used for calculation of production yield using SRIM code for stopping power of 67Cu via a given reaction over a certain energy range. Numerical valves of production yield in MBq/μA and particle energies in MeV were obtained from eqn. (1). We give the thick target yield from Figures 4-6.
Analysing the three graphs above, for proton induced reaction on 70Zn, the calculated integral yield of 67 C; at 17 MeV it amounts to 6.6 MBq/μAh. In comparison, the ongoing CRP of the IAEA recommends 2.70 MBq/μAh at the same energy and Hussain reported 2.40 MBq/μAh at the same energy. In case of protons on 68Zn, the calculated yield at 35 MeV is 2.20 MBq/μAh, increasing to 4.08 MBq/μAh for 40 MeV protons. According to the CRP of the IAEA, the recommended values of integral yields for this reaction over the same energies are 1.61 MBq/μAh and 2.30 MBq/μAh. In the same energy range, Hussain had previously calculated the integral yield of 67Cu as 2.0 MBq/μAh and 3.8 MBq/μAh. Similarly, for α-particles on 64Ni, the calculated integral yield in this work was 26.5 kBq/μAh at 15 MeV, increasing to 168 kBq/μAh for 20 MeV α-particle beams. Hussain and Qaim had previously calculated from their own data the yield of 67Cu as 25.3 kBq/μAh and 167 kBq/μAh at 15 and 20 MeV respectively.
Comparison of production routes of Copper-67
The production of the medical radionuclide 67Cu is possible via the reactions 64Ni (α, p) 67Cu, 68Zn (p, 2p) 67Cu and 70Zn (p, α) 67Cu. The corresponding particle energies and evaluated reaction cross section values are mentioned. The production possibility in different energy regions via different nuclear reactions has been clarified. The study of all reactions for the production of 67Cu leads to the conclusion that the 70Zn (p, α) 67Cu reaction should be the method of choice if cyclotrons of low energy are available. The major advantage of this route is the radiochemical purity of the product. The other drawback is the cost of enriched 70Zn target that is rather high. The 68Zn (p, 2p) 67Cu reaction is more favourable if high energy proton beams would be available. But the proton irradiation of enriched 68Zn gives large amounts of 67Ga along with 67Cu. Both the 67Cu and 67Ga have almost identical gamma-ray spectrum so a very clean separation of 67Cu is necessary. The least important is the 64Ni (α, p) 67Cu process. It gives low yield of 67Cu and the cost of the enriched target material is very high.
Comparison of Thick Target Yields Obtained by Simpson Numerical Integration (S.N.I) Method and Standard Integral (S.I) method for 70ZN (p, α) 67CU Reaction
Using the derived thick target radioisotope production yield equation in chapter three (eqn. (3)) and assuming some constant values for the irradiation time and target thickness, a relationship between the thick target yield obtained by Simpson numerical integration method and standard integral method were establish. Values of the thick target yield within the same energy ranges for 70Zn (p, α) 67Cu reaction leading to the production of copper-67 are tabulated in Table 1 above. It can be observed in the table that, the thick target yield values in both methods are almost the same. This implies that in the absence of appropriate nuclear reaction model code and the SRIM software package to generate cross section and stopping power values that demands the usage of the Simpson numerical integration for calculation of production yield, one can employ the standard integral method to obtain almost the same values as obtained by Simpson numerical integration.
Table 1. Particle energy and thick target yield values for S.N.I and S.I.
| Energy(MeV) | Thick Target yield(MBq/ÃÆââ¬Å¡ÃâõA) | ||
|---|---|---|---|
| Ein | Eout | Simpson Integration Method | Standard Integral Method |
| 8 | 2.5 | 0.20 | 0.20 |
| 9 | 2.5 | 0.50 | 0.45 |
| 10 | 2.5 | 1.10 | 1.10 |
| 11 | 2.5 | 1.90 | 1.90 |
| 12 | 2.5 | 4.60 | 4.56 |
Copper-67 is a very important medical radioisotope. The study compared both experimental and theoretical data with the new version of Talys code 1.6 of which good agreement exit between them. Furthermore, the integral or thick target yields are estimated based on the measured excitation functions for all the investigated reactions of which the 70Zn (p, α) 67Cu reaction is the method of choice if low energy cyclotron are available. The optimum energy range for this reaction is 18-13 MeV and the thick target yield has been estimated with the same optimum energy of 6.3 MBq/μAh.
The authors are much grateful to School of Nuclear and Allied Sciences and members of Ghana Atomic Energy Commission for their assistance in the course of this research work.