Stochastic Generation of Spatially Consistent Monthly Rainfall
Using SCL

Rahman Abdul A

Stochastic Generation of Spatially Consistent Monthly Rainfall Using SCL

Rahman Abdul A^*

Department of Physics, Faculty of Science, COMSATS Institute of Information Technology, Pakistan

*Corresponding Author:: Abdul AR
Department of Physics, Faculty of Science
COMSATS Institute of Information Technology, Pakistan
Tel: +92 51 9247000
E-mail: andulrahman.aftabafzal@gmail.com

Received Date: 21/01/2018; Accepted Date: 14/03/2018; Published Date: 23/03/2018

Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics

Abstract

Rainfall is the primary and most important component of any hydrological event. There is some amount of uncertainty in the future prediction of rainfall. The purpose of using SCL is the quantification of uncertainty involved in the prediction of rainfall. In the last few decades a considerable variation in the rainfall of the northern Pakistan has occurred. This might be due to the increase in temperature which is going to be threat for the water resources of Pakistan. So there is need to estimate the uncertainties involved in the estimation of the rainfall. In this paper an effort is being carried out to quantify the uncertainties in the average monthly rainfall for UIB using SCL (Stochastic Climate Library). In this paper an effort is being done to quantify the uncertainty involved in the average monthly rainfall data of rain gauge in Astor. Using the SCL the stochastic data is generated based upon the previous average monthly rainfall data of Astor from (1954 to 2000). Several statistics (annual and monthly) are computed to determine the behavior of the model and to compare them with the stochastic data produced.

Keywords

Environment, Regeneration, Agriculture, Hydrology

Introduction

Monthly rainfall data plays a key role in the estimation of runoff generated from large catchment and also to simulate the water resources of any country which is the backbone of the economy. In order to determine how a system will behave against the variation in the climate long data records of stochastically generated data are used.

Precipitation is vital in the climate variations. Srikanthan and Pegram [1] described an increasing trend in the precipitation to 1% from 0.5% in the elevated areas of the northern Pakistan. This increase has been observed in every decade of the 20th century. The statistically insignificance trend in the rainfall all over the world as well as for Himalayas being studied by many researchers in the last century.

Average monthly precipitation data is required to simulate the monthly flows which are main component of runoff produced from large catchments. But these models have a drawback that these models do not work well for the catchments which have considerable number of dry months. McMahon and Srikanthan [1] described the method of fragments to separate the annual rainfall data into its constituents by using the AR model of order 1. The limitation of this method is the inability that it cannot preserve the correlation (monthly) between the 1st month of a year and previous month of last year and also the same patterns for shorter length of data records.

Using stream flows Perera and Maheepala [2] made few changes in the method of fragments that take care of the first limitation of preserves of the monthly correlation. For the second limitation they have used the Thomas-Fiering monthly (stream flow) model. But it becomes troublesome for the sites having considerable number of months having no rainfall.

O’Neill and Sharma [3] used nonparametric method to model the inter annual effects in monthly runoff.

Climate Variability Program in the Cooperative Research Centre (CRC) for Catchment Hydrology has developed and tested many computer programs for generating stochastic climate data at time scales from less than one hour to one year and for point sites to large catchments. The appropriate models are part Stochastic Climate Library. In this research paper the development and testing of annual and monthly data of Astore (Pakistan) station has been studied. Stochastic monthly data can be further used for hydrological modelling and to quantify the uncertainties in the environmental system. A first order Markov chain is used which consist of two parts one is to model the occurrence of rainfall and second is to find the depth of occurrence. A two parameter Gamma distribution is used with correlated random numbers to obtain the rainfall depths. Historical and generated statistic shows that the model preserves the important characteristics of monthly and annual rainfall. Bardossy et al. [4] have studied time series of circulation patterns which are modelled with the help of a semi-Markov field and Rainfall is linked to the circulation patterns using conditional probabilities. Bardossy et al. [4] estimated the parameters method based on the moments of the observed data are developed.

In the last few decades a considerable variation in the rainfall of the northern Pakistan have occurred [5]. This might be due to the increase in temperature which is going to be threat for the water resources of Pakistan. So there is need to estimate the uncertainties involved in the estimation of the rainfall. In this paper an effort is being carried out to quantify the uncertainties in the average monthly rainfall for UIB using SCL (Stochastic Climate Library).

Study Area

In this study Astore watershed is selected to determine the uncertainty in the prediction of rainfall [6]. The Astore watershed is located in Pakistan having longitude and latitude 35° 33’ and 74° 42’ respectively, having a catchment area of about 3990 km² Figure 1. There is only one gauging station installed by Pakistan Metrological Department having an elevation of 2168 m.a.s.l.

Figure 1: Astore Water Shed.

A store watershed is an elevated area having peak elevation of about 8000 m.a.s.l. in winter it is mostly covered with snow and glaciers. About 15% of the total area is covered with snow [7,8].

Methodology

MMF (Modified Method of Fragments) and AR (1) Model

The historical data of average monthly rainfall is standardized yearly in such a way that sum of average monthly precipitation for any year is one [9,10]. This can be done by dividing the average monthly rainfall by respective annual precipitation. In this way by having the record of k years one can produce the k sets of fragments of average monthly rainfall.

The appropriate number of monthly fragments for a particular year, n, is obtained by taking in account how close the produced yearly rainfall data and the monthly precipitation data for the last month of previous year to the corresponding observed data [2] (Figure 2). It is done by having of the appropriate number of the monthly fragment of a year, z, in the produced monthly data series that will develop a minimum value αz, that is given here:

pure-and-applied-physics-auto-correlation

Figure 2: Historical and Stimulated data of Rainfall in terms of Mean, Standard deviation, skewness, lag one auto-correlation, maximum and minimum.

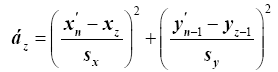
: Produced annual rainfall for year n

x_z : Observed annual rainfall for year n

s_x : st. dev of the annual precipitation

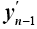: Observed monthly precipitation for the last month of the year n-1

y_z-1: Observed monthly precipitation for the last month of the year z-1

s_y= st. dev of the monthly rainfall for the last month of the year

The annual rainfall is generated by Autoregressive model of order 1 (AR (1)).

Monthly Parameters

The average values of the mean, std. dev, skewness, lag one autocorrelation max, min and percentage zero rain for the 100 replicates are compared with the historical values and are shown from Tables 1-7.

Table 1. Comparison between Historical and Generated monthly mean rainfall.

Item	Hist.	Mean	2.50%	25%	50%	75%	97.50%	Tol.	Y/N
Jan	43.349	38.871	28.571	35.676	38.536	42.201	47.148	7.50%	N
Feb	48.677	43.645	35.759	41.085	43.785	46.771	52.36	7.50%	N
Mar	88.632	91.138	72.932	82.783	89.691	98.238	120.49	7.50%	Y
Apr	89.609	89.4	74.925	81.03	88.581	95.362	110.684	7.50%	Y
May	76.823	81.489	63.354	74.763	81.302	88.013	97.98	7.50%	Y
Jun	24.323	24.767	18.859	22.469	24.467	27.081	32.769	7.50%	Y
Jul	24.349	25.069	18.98	22.587	24.93	27.418	32.312	7.50%	Y
Aug	25.687	27.875	20.833	25.208	27.485	30.169	35.959	7.50%	N
Sep	21.106	20.229	14.412	17.354	19.479	22.604	30.058	7.50%	Y
Oct	28.731	32.639	21.829	27.996	32.282	36.489	45.568	7.50%	N
Nov	21.188	21.14	15.97	18.314	20.876	23.369	27.607	7.50%	Y
Dec	29.974	29.917	22.483	27.261	29.433	32.616	37.844	7.50%	Y

Table 2. Comparison between Historical and Generated monthly mean rainfall Standard Deviation.

Item	Hist.	Mean	2.50%	25%	50%	75%	97.50%	Tol.	Y/N
Jan	30.13	29.49	20.39	26.669	29.208	31.96	38.569	7.50%	Y
Feb	29.692	29.881	24.433	27.009	30.067	32.583	36.797	7.50%	Y
Mar	57.134	61.978	44.357	55.788	63.38	67.087	83.297	7.50%	N
Apr	53.213	53.854	45.017	49.409	53.754	58.348	63.438	7.50%	Y
May	59.619	61.62	44.622	57.155	61.56	65.61	77.15	7.50%	Y
Jun	19.899	19.774	13.698	15.887	19.245	22.47	29.536	7.50%	Y
Jul	22.796	21.107	12.474	18.336	21.516	23.508	30.671	7.50%	Y
Aug	22.993	24.207	15.2	21.493	23.942	27.107	32.805	7.50%	Y
Sep	26.595	22.449	9.647	13.06	25.13	27.257	40.771	7.50%	N
Oct	33.02	38.068	20.373	33.062	38.402	43.957	51.624	7.50%	N
Nov	23.678	22.293	15.644	20.169	22.412	25.1	28.712	7.50%	Y
Dec	31.051	28.644	21.362	25.299	28.389	31.293	40.631	7.50%	N

Table 3. Comparison between Historical and Generated monthly mean rainfall Skewness.

Item	Hist.	Mean	2.50%	25%	50%	75%	97.50%	Tol.	Y/N
Jan	-0.139	-0.022	-0.21	-0.1	-0.031	0.058	0.197	±0.2	Y
Feb	-0.024	0.008	-0.194	-0.055	0.008	0.075	0.208	±0.2	Y
Mar	-0.06	-0.057	-0.342	-0.145	-0.057	0.04	0.232	±0.2	Y
Apr	-0.045	-0.072	-0.339	-0.204	-0.083	0.045	0.294	±0.2	Y
May	0.002	0.104	-0.119	0.007	0.104	0.167	0.364	±0.2	Y
Jun	-0.072	0.011	-0.285	-0.166	-0.001	0.145	0.395	±0.2	Y
Jul	-0.064	-0.059	-0.203	-0.147	-0.091	-0.008	0.23	±0.2	Y
Aug	-0.105	0.021	-0.271	-0.088	0.004	0.113	0.384	±0.2	Y
Sep	0.068	0.018	-0.201	-0.104	-0.008	0.117	0.362	±0.2	Y
Oct	-0.116	-0.084	-0.275	-0.162	-0.108	-0.036	0.194	±0.2	Y
Nov	0.07	0.086	-0.129	0.004	0.081	0.143	0.346	±0.2	Y
Dec	-0.029	0.014	-0.241	-0.107	0.002	0.116	0.327	±0.2	Y

Table 4. Comparison between Historical and Generated monthly mean rainfall lag one autocorrelation.

Item	Hist.	Mean	2.50%	25%	50%	75%	97.50%	Tol.	Y/N
Jan	143.1	134.947	77.592	130.665	140.257	144.96	150.074	10%	Y
Feb	144.4	126.583	87	91.899	140.859	151.325	157.418	10%	N
Mar	239.8	253.6	222.516	245.346	252.145	256.373	299.613	10%	Y
Apr	221.2	210.554	168.11	190.149	217.351	228.006	241.5	10%	Y
May	248.7	246.539	205.652	233.352	240.523	255.409	311.121	10%	Y
Jun	94.1	87.641	47.582	56.994	93.719	102.147	133.051	10%	Y
Jul	116.3	101.828	49.557	88.542	107.286	117.702	145.49	10%	N
Aug	106.6	104.477	62.156	105.129	107.78	109.351	112.368	10%	Y
Sep	172.3	121.793	47.445	55.575	168.877	174.539	180.697	10%	N
Oct	170.6	171.305	93.849	172.43	184.684	191.094	198.838	10%	Y
Nov	110	99.698	70.548	81.182	109.537	112.169	114.77	10%	Y
Dec	168.1	128.26	81.035	96.23	128.854	164.077	171.866	10%	N

Table 5. Comparison between Historical and Generated monthly rainfall maximum.

Item	Hist.	Mean	2.50%	25%	50%	75%	97.50%	Tol.	Y/N
Jan	2.3	2.635	0.91	1.983	2.196	3.294	6.867	10%	N
Feb	4.2	4.103	3.821	3.95	4.078	4.176	5.011	10%	Y
Mar	9.7	10.961	2.48	8.059	9.092	11.446	23.959	10%	N
Apr	1.3	4.218	1.281	1.299	1.326	2.981	21.431	10%	N
May	4.5	6.14	3.195	4.3	4.43	4.611	14.355	10%	N
Jun	2	2.119	1.42	1.966	2.036	2.275	2.863	10%	Y
Jul	0.3	0.475	0.262	0.272	0.294	0.795	0.999	10%	N
Aug	2.2	2.535	1.703	2.107	2.242	3.206	4.355	10%	N
Sep	0.8	1.267	0.754	0.778	0.799	2.224	3.108	10%	N
Oct	0.3	0.865	0.272	0.284	0.3	1.394	2.56	10%	N
Nov	0.3	0.378	0.287	0.293	0.3	0.313	1.315	10%	N
Dec	0.8	1.047	0.725	0.782	0.816	1.213	1.867	10%	N

Table 6a. Comparison between Historical and Generated monthly rainfall minimum.

Item	Tol.	Y/N
Jan	±5	Y
Feb	±5	Y
Mar	±5	Y
Apr	±5	Y
May	±5	Y
Jun	±5	Y
Jul	±5	Y
Aug	±5	Y
Sep	±5	Y
Oct	±5	Y
Nov	±5	Y
Dec	±5	Y

Table 6b. Comparison between Historical and Generated monthly rainfall% no rain.

Item	Tol.	Y/N
Jan	±5	Y
Feb	±5	Y
Mar	±5	Y
Apr	±5	Y
May	±5	Y
Jun	±5	Y
Jul	±5	Y
Aug	±5	Y
Sep	±5	Y
Oct	±5	Y
Nov	±5	Y
Dec	±5	Y

Table 7. Comparison between Historical and Generated monthly rainfall Statistics.

Statistics	Hist.	Mean	2.50%	25%	50%	75%	97.50%	Tol.	Y/N
Rainfall mean	522.448	526.179	469.49	506.27	522.248	544.539	596.525	5%	Y
Rainfall St.dev	130.623	139.548	93.109	121.293	138.622	154.408	196.575	5%	N
Rainfall Skewness	0.378	0.363	-0.539	-0.059	0.284	0.661	1.766	±0.5	Y
Rainfall lag oneautocorrelation	-0.075	-0.069	-0.464	-0.18	-0.058	0.048	0.277	±0.15	Y
Rainfall max	1.642	1.685	1.362	1.543	1.629	1.755	2.297	10%	Y
Rainfall min	0.538	0.467	0.092	0.384	0.494	0.575	0.687	10%	N
Two year low rainfall	1.42	1.24	0.582	1.131	1.299	1.393	1.567	10%	N
Three year low rainfall	2.322	2.108	1.37	1.986	2.183	2.299	2.514	10%	Y
Five year low rainfall	4.157	3.937	2.967	3.775	3.984	4.159	4.493	10%	Y
Seven year low rainfall	6.1	5.816	4.822	5.574	5.871	6.062	6.455	10%	Y
Ten year low rainfall	8.756	8.707	7.742	8.45	8.784	8.988	9.378	10%	Y

Annual Parameters

The mean values of average, standard deviation, skewness, lag one auto correlations, max, min and two, three, five, seven and ten years low rainfall from 100 replicates are shown in the Table 7.

Results and Conclusions

The main concern of the stochastic rainfall generation is rainfall depth and its occurrence. In this study a stochastic rainfall generation model for the average monthly rainfall is made for Astor. The monthly rainfall model can be applicable in the detailed water budget and environmental and agricultural model studies. The average monthly precipitation data from 1954 to 2000 was made for Astor. The model’s monthly and annual parameter is estimated using SCL (stochastic climate library). The Root mean square values calculated for average of the 100 monthly replicates shows fairly good results. The average values of % no rain for all the 100 replicates have zero values which shows that no month from the year 1954 to 2000 have zero rainfall for the Astor, whereas the historical data shows some month from 1954 to 2000 having zero average monthly rainfall. So on the basis of the comparison for the % no rain we can say that model is over estimating the % occurrence of no rain.

References

Srikanthan Rand Pegram GGS.Stochastic generation of multi-site rainfall occurrence. Advances in Geosciences. 2006;6:1-10.
Bardossy Aand Plate EJ.Modelling daily rainfall using a semi-Markov representation of circulation pattern occurrence. Journal of Hydrology. 1991;122:33-47.
Adamowsky K and Smith AF.Stochastic generation of rainfall. J. Hydraul. Eng. ASCE.1972;98:1935-1945.
Maheepala S and Perera CJC.Monthly hydrologic data generation by disaggregation. J. Hydrol. 1996;178:277-291.
Porter JW and Pink BJ.A method of synthetic fragments for disaggregation in stochastic data generation. Hydrology and Water Resources Symposium, Institution of Engineers, Australia.1991;187-191.
Sharma A and O’Neill R.A nonparametric approach for representing interannual dependence in monthly streamflow. Submitted to Water Resources Research. 2001.
Heneker TM, et al.A point rainfall model for risk-based design.Journal of Hydrology. 2001;247:54-71.
Lambert M and Kuczera G. Seasonal Generalized Exponential Probability Models with Application to Interstorm and Storm Durations. Water Resources Research. 1998;34:143-148.
Frost A, et al. Stochastic Generation of Point Rainfall Data aiSubdaily Timescales: A Comparison of DRIP and NSRP. Cooperative Research Centre for Catchment Hydrology.2004.
Stochastic Climate library user guide version 2.1b.

Item	Tol.	Y/N
Jan	±5	Y
Feb	±5	Y
Mar	±5	Y
Apr	±5	Y
May	±5	Y
Jun	±5	Y
Jul	±5	Y
Aug	±5	Y
Sep	±5	Y
Oct	±5	Y
Nov	±5	Y
Dec	±5	Y

Item	Tol.	Y/N
Jan	±5	Y
Feb	±5	Y
Mar	±5	Y
Apr	±5	Y
May	±5	Y
Jun	±5	Y
Jul	±5	Y
Aug	±5	Y
Sep	±5	Y
Oct	±5	Y
Nov	±5	Y
Dec	±5	Y

Item	Tol.	Y/N
Jan	±5	Y
Feb	±5	Y
Mar	±5	Y
Apr	±5	Y
May	±5	Y
Jun	±5	Y
Jul	±5	Y
Aug	±5	Y
Sep	±5	Y
Oct	±5	Y
Nov	±5	Y
Dec	±5	Y

Item	Tol.	Y/N
Jan	±5	Y
Feb	±5	Y
Mar	±5	Y
Apr	±5	Y
May	±5	Y
Jun	±5	Y
Jul	±5	Y
Aug	±5	Y
Sep	±5	Y
Oct	±5	Y
Nov	±5	Y
Dec	±5	Y

Item	Tol.	Y/N
Jan	±5	Y
Feb	±5	Y
Mar	±5	Y
Apr	±5	Y
May	±5	Y
Jun	±5	Y
Jul	±5	Y
Aug	±5	Y
Sep	±5	Y
Oct	±5	Y
Nov	±5	Y
Dec	±5	Y

Item	Tol.	Y/N
Jan	±5	Y
Feb	±5	Y
Mar	±5	Y
Apr	±5	Y
May	±5	Y
Jun	±5	Y
Jul	±5	Y
Aug	±5	Y
Sep	±5	Y
Oct	±5	Y
Nov	±5	Y
Dec	±5	Y