Study on the Capacitance between Orbitals and Atoms Modelling

Abstract

In this paper, we investigate the assumption that the orbital or energy level of an electron can be considered as an electrode of a tunnel junction. Based on this assumption, an electrical model – equivalent circuit – for atom's emission is presented and Hydrogen atom is taken as an example. Also the line spectra of Iron and Sodium are used to verify the model.

Keywords

Single-electron tunneling, Coulomb blockade, Bohr model, Atomic spectra, Atomic structure.

Introduction

Since 100 year, Niels Bohr suggested his model of the atom. He succeeded only in interpretation of line spectrum of single electron atoms (Hydrogen and ionized Helium) so more general model was still needed. In 1926, Erwin Schrödinger presented his famous equation which described complicated physical systems by the concept of wavefunction of the system but in many cases the solution of Schrödinger equation is not a routine process.

In this paper, we look to the atom from another point of view. The atom was considered as an electrical circuit and the measured line emission of the element is used to calculate the values of the components of equivalent circuit of the atom.

The next section investigates the analogy between the quantum tunneling of an electron through tunnel junction and transition across energy levels. In the third section, an electrical model for atom's emission is presented and the Hydrogen atom is taken as an example. The last section provides indications that the model of atom's emission may also valid for heavy atoms.

From Single Electronics to Bohr Model

Single electronics, controlling the transfer of one or few electrons along systems of small conducting particles "islands" which are separated by tunnel barriers, are promising ultralow power devices for high density integrated devices.

The field of solid state single electronics began in 1985 when Averin and Likharev apply the orthodox theory [1] on the transfer of discrete charge through energy barriers along metallic conductors separated by approximately 1 nm of insulating material, which is known as a "tunnel junction" [2]. In 1987, their theoretical work was supported by Fulton and Dolan experiments [3] when the first single electron transistor was implemented.

The physics of single electronics is based on the coulomb blockade concept. This means, to transfer one electron through a tunnel junction with capacitance C, the electron must overcome the charging energy barrier E_C [4], Coulomb blockade energy, where:

E_C = e²/2C (1)

The electromagnetic radiation with frequency f∼ E_C /h is generated as a photoresponse of single-electron systems [5], so that the wave length λ of the emitted photons can be expressed as follows:

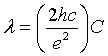(2)

Where h is the planks constant, c is the speed of electromagnetic wave in vacuum, C is the capacitance of the tunnel junction and the constant 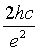equals 1.5477 × 10 mF^-1 . The wave length λ is wavelength of the emitted photon.

If the s orbitals of energy levels are considered to be conducting spheres and the maximum values of wavefunctions of the electron |Ψ |² – Bohr radiuses of the energy levels – are considered to be the radius of the spheres. The capacitance between two conducting concentrated spheres separated by vacuum is:

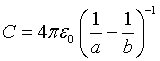(3)

where εo is the permittivity of the vacuum, and a and b are the diameters of the inner and outer spheres respectively. Substituting equation (3) in (2) and solving for 1/λ,

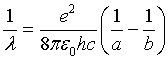(4)

Equation (4) is the same as Rydberg formula for Hydrogen before applying Bohr's role of quantizing the angular momentum. This means the electromagnetic wave emitted from the tunnel junction has the same wave length as the wave emitted from the atom if the electron in both cases tunnels through the same capacitance. According to this concept, equation (2) can be rewritten as follows:

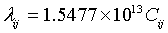(5)

Where λ_ij is the wave length of the emitted wave when electron "tunnels" from energy level j to i ( or the absorbed wave when electron "tunnels" from energy level i to j) and C_ij is the capacitance between i and j energy levels.

The capacitance system of concentrated spheres looks like capacitors connected in series (Tunnel junctions in series in the case of atoms):

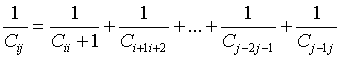(6)

Using equation (5), equation (6) can be rewritten as

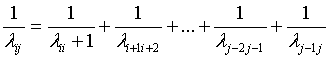(7)

The last equation can be verified by finding the relations between the line spectrum wave lengths of the investigated element.

Electrical Model for Hydrogen Atom

The values of any series of line spectrum can be predicted by substituting the values of the previous series in equation (7). So the complete spectrum can be predicted if the first series is known. Figure 1 illustrates the proposed model for the Hydrogen atom (It looks like tunnel junctions turnstile). The capacitances between energy levels can be computed by substituting the first values of the line spectrum series, stated in Table 1 for Hydrogen atom, in equation (5). The capacitances C₁₂ to C₆₇ in Table 2 are computed directly by substituting the first terms of the series listed in Table 1 in equation (5). Equation (7) is used to compute the capacitances C₇₈ to C₁₁.

Figure 1: Proposed model for Hydrogen atom.

Table 1: Line spectrum series of Hydrogen atom (wavelengths in nanometers).

Table 2: The computed capacitances between energy levels of Hydrogen atom.

Iron and Sodium Electrical Models

Figure 2 shows the line spectra of Hydrogen, Helium, sodium, and Iron [6]. The first series of Hydrogen and Helium spectra do not overlap with the second one, so the complete spectra of them can be computed. But for heavier atoms, for example Sodium and Iron, the series of spectra overlap with each other.

Figure 2: The ultraviolet and visible emission spectra of Gaseous Hydrogen, Helium, Sodium and Iron [6].

To validate our model and equations for heavy atoms, we try to find frequencies that agree with equation (7).

The obtained results are:

For Sodium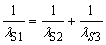

For Iron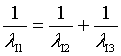

These results show that equation (7) is valid for heavy atoms as it is for Hydrogen atom.

Conclusion

In this paper, we have introduced some concepts which show that the inter-orbitals capacitance can be used to develop an equivalent circuit to the atom. For Hydrogen atom, this is completely true. Also for heavier atoms, like Sodium and Iron, some computations tell us that our direction is right but more investigations need to be done to validate the theory.

As a result of this paper, the spectrum of an element can be theoretically computed based on a part of it. The electrical model of atoms may explain some unclear phenomena of the chemical reactions.

References

1. Kulik IO and Shekhter RI.Sov PhysJETP.  1975; 41:308.
2. Averin DV andLikharev KK.SQUID’85,H. Lubbig and H.D. Hahlbohm, Eds.,W. deGruyter, Berlin. 1985;  197.
3. Fulton TA and Dolan GJ.Phys Rev Lett. 1987; 59: 109.
4. Berman D. Ph.DThesis, MassachusettsInstituteofTechnology, 1998.
5. Likharev KK and Devyatov IA.PhysicaB.1994; 1341: 194-196.
6. http://chemed.chem.wisc.edu/chempaths/GenChem-Textbook/The-Visible-and-Ultraviolet-Spectra-of-Molecules-Molecular-Orbitals-1040.html