ISSN: 2320-2459
ISSN: 2320-2459
B.P. Konstantinov Petersburg Nuclear Physics Institute, Gatchina, 188300 Russia
Received Date: 08/02/2017; Accepted Date: 17/02/2017; Published Date: 24/02/2017
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
The angular distributions of double charged fragments of a nucleus 16Þ with the momentum 4.5àGeV c-1 and 208Pb with the momentum 160àGeV c-1 were studied during their interaction with photoemulsion nuclei. Contrary to common belief that fragmentation of relativistic nuclei in a wide range of masses and energy conforms to the statistical model, the experimental angular distributions of double charged fragments of these nuclei are not described by this model.
Fragmentation, Photo emulsion, Orthogonal axis, Emission
Abundant experimental material on the fragmentation of nuclei was accumulated from the moment of its discovery up to the
present; however it does not provide the clear understanding of this phenomenon. A number of studies [1-5] stated conformity of the experimental results expected from the statistical model. According to this model nucleons in a nucleus have the momentum
distribution ~ exp (P2/2σ0) [6]. P – Nucleon momentum in a nucleus, momentum distribution dispersion. Value of σ0 is estimated
either by the Fermi momentum РF: σ0=PF/51/2, or by a nucleus radius (R=r0A1/3): σ0=(9π)1/3ħ/(2r051/2) [7]. For a fragment
with the mass number AF momentum distribution dispersion is represented by 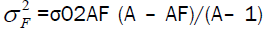 [6]. For isotropic
momentum distribution of a fragment in a nucleus, dispersion of its momentum projection onto any orthogonal axis will be equal
to [6].
[6]. For isotropic
momentum distribution of a fragment in a nucleus, dispersion of its momentum projection onto any orthogonal axis will be equal
to [6].
According to the hypothesis of limiting fragmentation [7] the nuclei fragments preserve their momentum values, which they had prior to the nucleus fragmentation. On account on the smallness of transverse momenta and the presence of high transportation velocity of fragments of relativistic nuclei, the fragments can be positively traced to the primary nucleus. Measuring the fragments' emission angle with orthogonal axes allows one to estimate the projections of their momenta on this axis using a formula:
Рi=Р0∙АF∙sinφi=Р0∙АF∙φi (in view of the smallness of φ)
Р0 – momentum of a nucleon of a fragmenting nucleus,
АF – fragment mass number,
φi – the angle with one of the with orthogonal axes
and to compare with the predictions of the statistical model.
The projection angles of particle tracks either onto the emulsion plane Х0Y or onto the perpendicular X0Z plane are the immediately observed values in fragmentation of relativistic nuclei experiments. These angles define the projection of the fragment momentum with the mass number АF onto one of the Cartesian axes of a coordinate system Рi=Р0 АF sinφi, where Р0 – mom entum of a nucleon of the fragmenting nucleus, φi – the projection angle of a fragment with the axis i of the coordinate system.
To measure the angles the irradiated emulsion layer is places on the microscope table. The origin of the microscope coordinates is matched with the event center, and the 0Х axis is orientated towards the primary track. Then, moving away from the center of the events in the direction of secondary particles, the coordinates Xi, Yi , Zi are written down on the tracks of particles under investigation. Afterwards, according to a trivial task of vector algebra, the coordinates of vector origin and end are used to find the projection angles of tracks φi=tgφi=(Yi – Y0)/( Xi – X0) in the XY plane and αi=tgαi=(Zi – Z0)/( Xi – X0) in the XZ plane. However, this results in an inadvertent error, since the tracks have occasional S-shaped distortions caused by the deformation of emulsion in the course of its treatment in both horizontal and vertical planes. In the vertical plane the distortions increase because of the mechanical shrinkage of the emulsion layer, when the undeveloped silver bromide is extracted from it. Besides, the relativistic nucleus during its interaction with the target nucleus is scattered as a whole, which results in its deviation from the original direction.
It is possible to dispose of these errors if not the angle of individual fragments but the angles of pairs of fragments are considered φi j=|φi – φj |=|(Yi – Yj)/( X – X0)|, αi j=|αi – αj |=|(Zi – Zj)/( X – X0)| (if the measuring points are the same distance X from the center of the event). In this case, the errors caused by the deformation of the emulsion are significantly reduced, for the distance between tracks in the measuring point is just microns. The coordinate system does not affect the pair angles either. These angles are caused by the processes inside the nucleus and do not depend on the measurement method. Angle measurement error φi j and αi j depends only on the coordinates measurement accuracy. σ(φi j)=σ(Y)/X, σ(αi j)=σ(Z)/X.
In this work the primary measurements on the fragmentation of relativistic nuclei of oxygen and lead are analyzed, carried out in and presented by their author, accordingly. To measure the point position on the fragments traces, which are used to measure their emission angles in the emulsion plane, the microscope МПЭ-11 was employed with the position read-off into the computer. The division value of the sensors on the 0X and 0Y axes was determined by multiple measuring of a 10 μm segment of the object micrometer and equals 1,25 and 0,02125 μm accordingly.
Fragmentation of a Relativistic 16О Nucleus with the Momentum 4,5A GeV/s
Results
The measurements [4] were made in an emulsion chamber irradiated by the oxygen ions with the momentum 4.5A GeV/s in the Laboratory of High Energy Physics at JINR (Dubna). The search for events was carried out by tracking the traces of a primary particle. In total 146.47 m of traces were tracked. 1121 events of inelastic interaction of a primary nucleus with the emulsion nucleus were found throughout this length. Of all the events only 229 "pure" events were selected for measurements (those containing only relativistic clusters of a primary nucleus), which contain two or more double charged fragments of a primary nucleus. In this work the events with two, three, and four double charged fragments of a primary nucleus are reviewed separately. They turned out to be 134, 81, and 14 respectively.
Figure 1 shows the distribution of paired angles in events with two, three, and four double charged fragments. The results of the approximation of experimental distribution by normal probability distribution using the software program Origin Pro 7.0 is shown in Table 1.
Table 1. Parameters of approximating functions.
| σ(φi j)=9,3 ± 0,5 mrad | χ2=0,95 | (2α) | |
| σ(φi j)=9,5 ± 0,5 mrad | χ2 | =0,94 | (3α) |
| σ(φi j)=6,1 ± 0,5 mrad | χ2 | =0,86 | (4α) |
Fermi momentum for a nucleus 16О equals 230 MeV/s [5]. Parameter σ for a nucleon is 102,86 MeV/s, and for 4Не σ(4Не)=184 MeV/s. For the isotropic momentum distribution in a nucleus σ(РХ)=σ(РY)=σ(РZ)=σ(Р) [4] and, consequently, σ(РY(4Не))=184 MeV/s. Since РY(4Не)=Р0∙А(4Не)∙sinφ=Р0∙А(4Не)∙φ, thus
σ(φ)=σ(РY(4Не))/ Р0/А(4Не)=10,22 mrad.
φ i j=φi – φj and fragments i and j are emitted independently from each other. Consequently,
σ(φi j)=σ(φ)=14,45 mrad,
Which does not correspond to the obtained experimental result.
Therefore, not in a single group of the investigated events the statistical model of nuclei fragmentation does not describe the momentum distribution of double charged fragments in a fragmentation of a 16О nucleus.
Discussion of the obtained results
In a study [3] the creation and role of the nuclei 8Ве in fragmentation of light nuclei and the possibility of channel 16О → 2 8Ве → 4α realization is stated at the fragmentation 16О, equivalent to 28%. If the double charged fragments are formed from 8Ве, in this case we have two-body decay and the maximum angle between two fragments is known beforehand. 8Ве has 4 levels, decaying into α-particles: primary 0,092 MeV, 2,94 MeV, 11,4 MeV и 20,2 MeV [4]. The maximum angles between α-particles, corresponding to these energies are: 2,06 mrad, 11,64 mrad, 22,92 mrad and 30,52 mrad respectively.
On that basis, it could be presumed that double charged fragments in events with two such fragments emerged from 8Ве. But the distribution in all pairs of fragments in a group of events with three double charged fragments has the same parameters as the distribution in a group with two fragments. In a group with three fragments only one pair of fragments out of three can be related to 8Ве, in other words the distribution “3α” is primarily filled with false with regards to 8Ве pairs of double charged fragments. Therefore, the maximum angle between two fragments cannot serve as a reliable criterion that a pair of fragments is attributed to 8Ве. Subsequently, in the “2α” distribution not all the double charged fragments are connected with 8Ве.
The distribution of paired angles in the group of events with four double charged fragments is also mostly filled with false events, as in every event there may be only two pairs of fragments related to 8Ве, and there are six of them in the event, that is there is twice the number of false (not related to 8Ве) pairs, and it is qualitatively different from the distributions in groups of two and three double charged fragments. It can be assumed that the events in different groups are attributed to different processes inside the nucleus. This idea arises during an individual consideration of events with four double charged fragments.
Two groups of events are eyed during a visual observation of events with four doubly charged fragments. Two pairs of tracks can be clearly distinguished in one of them, which can be identified with the 8Ве decay from its ground state. A grouping of three fragments and their isolation from the fourth are observed in another group of events. It is shown in Figure 2.
The grouping of three double charged fragments can be identified with the excited state of 12С. This assumption follows from the observation (during the search for events) of “clean” two- fragment events. One of the fragments is a α-particle. The second one, according to the charge conservation, must be 12С, in other words the channel 16О → α + 12С is observed. But 12С may be not only in the ground state and therefore can contribute to all groups of regarded events in accordance with the processes 12С* → 3α, 12С* → рαLi and 12С* → ptαα. Similar ensembles of clusters of a 12С nucleus were observed in its photodisintegration [5,6]. Their presence was due to the effect of Feynman diagrams:
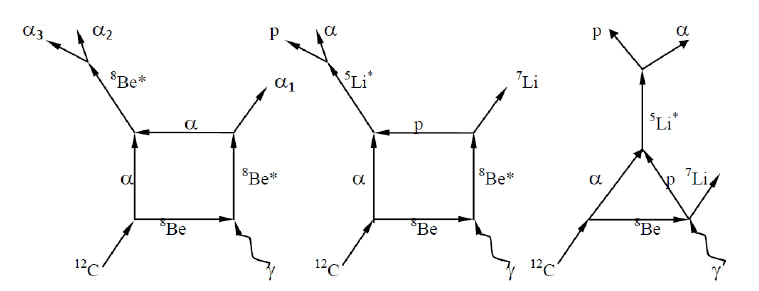
Including virtual resonance processes:

From the photodisintegration of a 12С nucleus it follows that it represents a structure of two clusters: α- a particle and a 8Ве nucleus. And the observed sets of clusters during its disintegration are associated with external effects and the intranuclear interaction.
It is in line with the cluster (α8Be) state model with the energy 7.65 MeV of a 12С nucleus, proposed as an explanation for the astrophysical process of carbon reproduction [7,8] and experimentally-confirmed during the study of the reaction 12С (12С,3α)12С.
In the search for events (with 2 – 4 α particles) the "pure" events of a type 16О → Li + B and 16О → p + N were also observed. The Li fragment was identified by its disintegration into three single-charged fragments. The excited states of Li, В and N can contribute to the double charged fragments under consideration.
The visual identification of the measured four-fragment events shows that five events are identified with the process 16О → 2 8Ве → 4 α, while nine events can be attributed to the process 16О → α + 12С* → α + 3 α. The examples of such events are shown in Figure 2.
The fragmentation of 16О nuclei with double charges fragments according to the visual observation can include the processes:
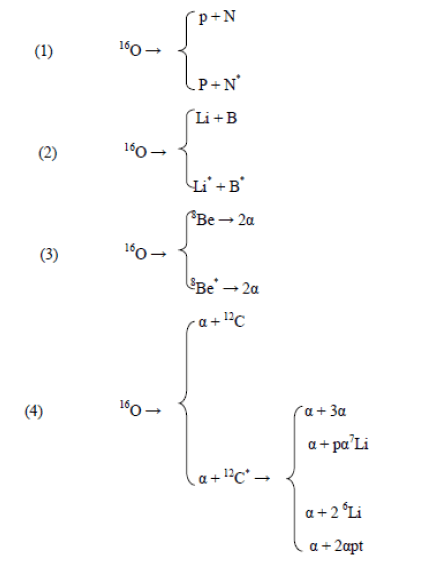
And the 16О nucleus itself can represent one of: (р+N), (Li+ B), (Be+Be) и (He+C) virtual cluster structures in a dynamic state. The observed ensembles of the 16О nucleus clusters emerge as a result of the electromagnetic effect of a target nucleus (virtual γ quantum) and the nuclear interaction inside 16О.
The experimental data analysis, as previously presented, [7] showed that the statistical model of fragmentation of relativistic nuclei does not describe the fragmentation of 16О nuclei with the momentum 4,5А GeV/c with double charged fragments. The possibility of channel 16О → 2 8Ве → 4 α implementation is not confirmed either. Even if it is assumed that all the measured events are determined by this channel, the probability is 19%.
Fragmentation of a Relativistic 208Рb Nucleus with the Energy 160A GeV
The measurements [6] are made in an emulsion chamber, irradiated by the lead ions with the energy 160A GeV, by means of scanning of the track throughout the length 87,402 m 1196 events were found, which contain two (and more than two) double charged fragments of a lead nucleus. Out of 1196 measured events 1145 with the number of double charged fragments from two to thirteen were selected for the analysis. 51 events were not selected for the analysis due to the visually observable failure in operation of the measuring equipment. The selected events were arranged in groups based on the number of double charged fragments in the event.
The categorization of the entire set of events and the parameters of their categorization into pair angles in each group are shown in Table 2.
Table 2. The categorization of the measured events based on the number of double charged fragments in the event and their parameters.
| Number of fragments in the event | Number of events | Number of pairs of fragments | σ, µrad | χ2 | NW2 | DN | |
|---|---|---|---|---|---|---|---|
| 13 | 2 | 156 | 691 | ± 40 | 0.95 | 0.1052 | 1.292 |
| 12 | 5 | 330 | 551 | ± 18 | 0.96 | 0.0752 | 0.832 |
| 11 | 6 | 330 | 643 | ± 33 | 0.92 | 0.225 | 1.804 |
| 10 | 20 | 900 | 559 | ± 21 | 0.97 | 0.0059 | 0.425 |
| 9 | 36 | 1296 | 644 | ± 19 | 0.98 | 1.491 | 2.545 |
| 8 | 60 | 1680 | 499 | ± 9 | 0.99 | 0.025 | 0.634 |
| 7 | 120 | 2519 | 554 | ± 11 | 0.98 | 0.2135 | 1.862 |
| 6 | 170 | 2550 | 566 | ± 11 | 0.99 | 0.2477 | 1.72 |
| 5 | 205 | 2045 | 572 | ± 14 | 0.98 | 0.3374 | 2.38 |
| 4 | 210 | 1260 | 614 | ± 17 | 0.98 | 0.2678 | 1.705 |
| 3 | 203 | 609 | 600 | ± 27 | 0.95 | 0.0910 | 1.259 |
| 2 | 108 | 108 | 674 | ± 20 | 0.76 | 0.0606 | 1.031 |
The Fermi momentum for the Pb nucleus is 265 MeV c-1 [1]. The σ0 parameter for a nucleon is 118,51 MeV c-1, and for 4Не σ(4Не)=235,296 MeV c-1. For the isotropic momentum distribution in a nucleus σ(РХ)=σ(РY)=σ(РZ)=σ(Р) and therefore σ(РY(4He))=235,296 MeV с-1. Since РY(4He)=Р0А(4Не) φ, then σ(φ)=σ(РY(4He))∕ Р0∕∕ А(4Не)=368 μrad, σ(φi j)=21/2 σ(φ)=520 μrad.
As can be seen, the obtained values σ(φi j) in all groups of events differ significantly (with respect to the measurement value) from those (520 μrad) expected from the statistical model.
There is some loss of statistical information [2] during the data histogramming. To assess the compliance of the experimental results with the expected ones, the expected distribution functions are compared to the experimental ones. The quantitative assessments of Cramér–von Mises-Smirnov and Kolmogorov criteria are shown in Table 2. Both criteria indicate the compliance of the experimental distributions in the groups of events with eight and ten double charged fragments with the expected one with the constant σ=520 μrad. And, therefore, it can be said that eight and ten double charged fragments leave the lead nucleus in accordance with the statistical model of fragmentation. But it could also mean that the statistical model is consistent with some real, yet unknown, mechanisms of production of eight and ten double charged fragments.
The distribution in the group of events with nine double charged fragments is not consistent with the expected significance level of <0,001 according to both criteria. This implies that these fragments are produced by the implementation of other mechanisms. There is no such clearness in other groups of events. In each group there exists a mixture of “statistically” born and foreign fragments in different proportions.
Considering the nucleus as a dynamic system of virtual states [2], the fragmentation of the lead nucleus is viewed as a complex and diverse process. The virtually isolated double charged objects in a nucleus can leave it statistically. At the same time there is fragmentation and interaction of other virtual objects. The resulting double charged fragments will have characteristics different from the first ones. It is impossible to identify the lead fragmentation mechanism (mechanisms) using only angular measurements of the fragments.
The analysis of experimental data presented previously [1] showed that the statistical model of the fragmentation of relativistic nuclei does not describe the fragmentation of nuclei of oxygen and lead with double charged fragments. The mechanisms of fragmentation of the oxygen nuclei can at least be assumed based on angle measurements and visual observation of all events of their inelastic interactions with emulsion nuclei. The lead nuclei fragmentation is associated with much more numerous processes. But it is not possible to identify them using the angular measurements only.
The author would like to thank F. G. Lepyohin for publishing the primary measurements on the fragmentation of the oxygen and lead nuclei, made by L.N. Tkach.