ISSN: 2322-0066
ISSN: 2322-0066
Samuel Bonaya Buya*
Mathematics/Physics teacher at Ngao girls, Secondary School, Kenya
Received date: 10/08/2017; Accepted date: 10/10/2017; Published date: 17/10/2017
Visit for more related articles at Research & Reviews: Research Journal of Biology
In this research the basis is established for solvability of the Galois group of a degree n polynomial. We establish that higher degree polynomials can in general be reduced to lower degree solvable forms. The lower degree root forms are then converted to higher degree form through conversion to what was identified as the nth order algebraic form of a root. Upon the basis of findings on solvability of higher degree polynomials a factorization method of solving higher degree polynomials is established.
We present a method of solving the sextic equation by converting it to a solvable factorized form. The factorized form will consist of two auxiliary cubic equations and their five parameters. The factorized form is selected such that four of its parameters are functionally related to the two parameters of the reduced sextic equation. The fifth parameter will be an identified rational number
Solving the Galois group of higher degree equations; Converting roots to nth order algebraic form; Algebraic solution of higher degree polynomial equations; Algebraic solution of the sextic equation
Literature Review
Sextic equations are part of polynomial equations. Polynomial equations have many real world applications. The aim of this contribution is to further contribute to understanding of methods of solving sextic equations.
From literature polynomial equations were first investigated more than four thousand years ago [1,2].
The general sextic equation takes the form 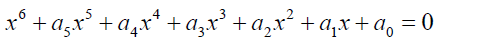 (1)
(1)
Abel and Ruffini showed that proved that it impossible to solve over a field of rational numbers [3].
Galois contributed to the solution of higher degree polynomials by giving the criterion by which they are solvable in radicals. According to Galois theorem f(x) is solvable in radicals if and only if its Galois group is solvable, see Rosen [3]. In this paper issues of solvability of the Galois group of higher degree polynomials will be critically looked into. Gaps in the approaches to solving of Galois groups of higher degree algebraic equations will be identified and sealed.
Edward Thabo Motlotle [4], in his 2011 master’s thesis managed to present a formula for solving the Bring-Jerrard quintic equation using the Newton’s sum formula. In his contribution Motlotle convincingly argued that Abel’s impossibility proof has been misconstrued by many as meaning that no general algebraic solution of the quintic equation is attainable. He showed that such a formula in unattainable only within a field of Rational numbers. He then moved on to deriving a formula. The importance this contribution is that formulae of higher degree polynomials are attainable at least over a field of algebraic numbers. Algebraic numbers include at least both radical and rational numbers. Algebraic numbers are solutions to polynomials with rational coefficients. The number field is constituted by both transcendental and algebraic numbers.
Thabo’s contribution is that for higher degree polynomial to have general solvable Galois group then the integral domain
F (containing the parameters) should also contain the roots in the extension field E.
A more recent contribution to the algebraic solution of quintic equation was given by Buya SB [5]. In this contribution the Bring-Jerrard quintic equation was factorized into auxiliary quadratic factors and with the parameters in the auxiliary factors correlated to the two parameters of the original trinomial quintic equation.
A method will be investigated of solving the trinomial sextic equation as a foundational basis for solving higher degree polynomial equations. The trinomial sextic will take the form:
x6 + px + q = 0 (2)
In this contribution a solvable factorized form of above sextic equation will be investigated. The equation will be factored into solvable cubic factors.
The factorized form will carefully be selected so that their parameters can be correlated to those of the above quintic equation. If the parameters of the two auxiliary cubic factors are a, b, d, e and f and those of the sextic equation are p and q, the sextic equation has general algebraic solution if four of the parameters of the cubic and quadratic factors are functionally related to the two parameters of the sextic equation and the fifth parameter is a rational number.
Theoretical Basis
Equations of the second, third, and fourth degrees, as is well known, may be solved with a finite number of radicals. It is argued that If, the equation is of higher degree than the fourth, this is, as a rule, no longer possible. The position has been that equations of the fifth or higher degrees must consequently be solved by other irrationalities than radicals [6].
In algebra the solution in radicals entails the splitting of the Galois group of an irreducible polynomial into a series of normal subgroups [7]. In this analysis a basis of solvability of higher degree polynomials will be established.
The following relationship holds between two roots of a quadratic equation.
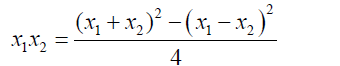 (3)
(3)
Consider the symmetric functions:
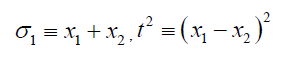 (4)
(4)
The Galois Group of a quadratic is S2.
x1 x2 =σ2 (5)
From the equations 4:
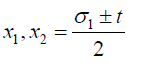 (6)
(6)
From 3
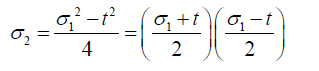 (7)
(7)
Thus the roots ×1 ,×2 are related to the symmetric functions σ1 and t and therefore they can be solved, see [7]
Let us consider the form 3 above. It can easily be generalized to the form:
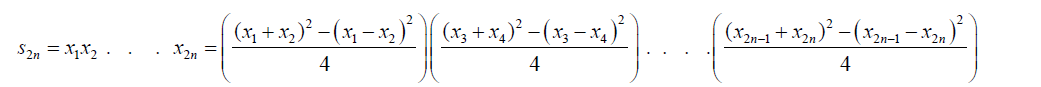 (8)
(8)
ÃÂÃâ¦2n is the Galois group of a polynomial function of degree 2n. In terms of symmetric functions the equation 8 can be written as:
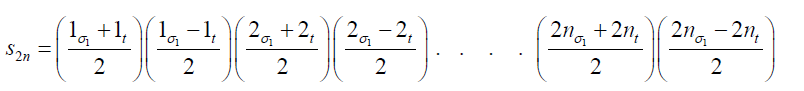 (9)
(9)
Thus the roots of a polynomial equation of degree 2n are:
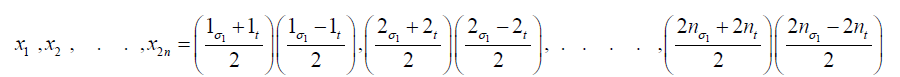 (10)
(10)
Theoretically therefore the Galois group of a polynomial equation of degree n can be split n times.
The general procedure for solvable polynomial is as follows: Starting polynomial coefficients exhibiting the symmetry of the
Galois group, we work down lowering the symmetry by reducing the size of the Galois group, until at the bottom the coefficients are related to the roots [7]. If that is the case then by the above reasoning higher degree polynomials are solvable.
The above analysis suggests that a good approach to solving higher degree polynomials is to reduce them to lower degree forms, possibly quadratic and cubic.
Quintic equations have been proven to have algebraic solution in general [4,5]. With the solvability of quintic equation it should be possible to extend the Bring-Jerrard transformation to eliminate four intermediate terms of the sextic equation to convert it to trinomial form.
In this paper I will consider the solution of the trinomial sextic equation:
x6 + px + q = 0 (11)
Before attempting an algebraic solution of the above trinomial sextic equation, it should be noted for a cubic equation:
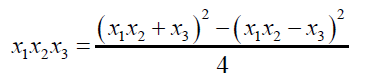 (12)
(12)
The above forms can be extended to higher degree polynomials. When extended to degree five polynomials then the Galois group can be split as follows:
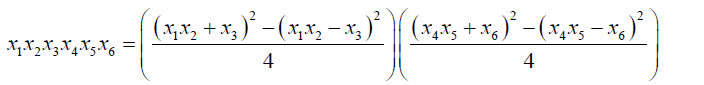 (13)
(13)
In attempting to solve the sextic equation the Galois group can be split further as follows:
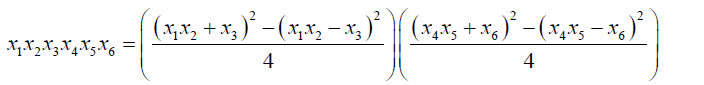 (14)
(14)
An extra note can be made is that the equations 8, 13, 1.4 and their extension can be used to make remarkable observations about integers e.g.
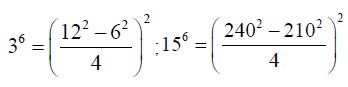 and so on. Put in other words:
and so on. Put in other words:
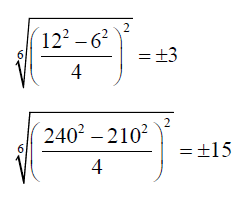
We can write the algebraic form to the order 6 of the number 15 as:
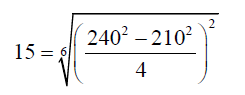
Thus in equation 14 for example if we put x1 = x2= x3= x4= x5= x6 then:
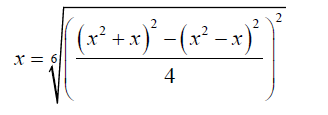 (15)
(15)
This is the algebraic form to the order 6 of a number x. Thus in general any number, rational or irrational can be written in algebraic form order n.
The significance of the step 15 is that if a polynomial equation of degree n is reduced to lower degree auxiliary polynomial
equations, the lower degree roots can be reconverted back to roots to the original degree via the concept of algebraic form to the order n.
With the prospect of algebraic solvability of higher degree polynomials thus clarified, the way forward for solution of the trinomial sextic equation would be by the method of factorization.
Consider the trinomial sextic equation:
x6 + px + q = 0 (16)
Factorized form selected:
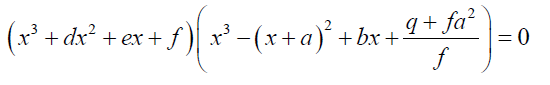 (17)
(17)
The form selected above is similar to that used by Buya S.B. [6] in his attempt to present a method to solve the general quintic equation.
If in the expansion of 17
The x5 coefficient equated to zero then
d =1 (18)
1) The ×4 coefficient is equated to zero and substituting 18 into the resulting equation:
b = 2a +1 (19)
2) The ×3 coefficient is equated to zero and substituting 18 then we obtain the equation:
q + f ( f − e − a2 +1) = 0 (20)
3) Equating the ×2 coefficient to zero and simplifying:
q + f (e − f ) = 0 (21)
4) Equating the x coefficient to p and simplifying:
eq + f2 = pf (22)
From 21:
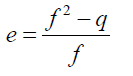 (23)
(23)
Substituting 23 into 22 and simplifying:
f3 + f2 (q − p) − q2 = 0 (24)
Taking
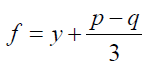 (25)
(25)
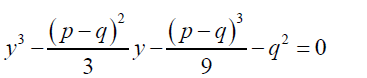 (26)
(26)
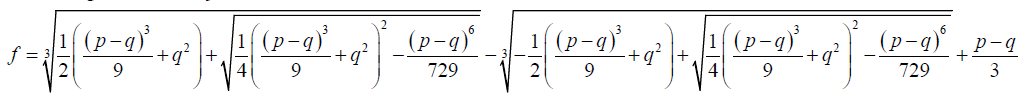 (27)
(27)
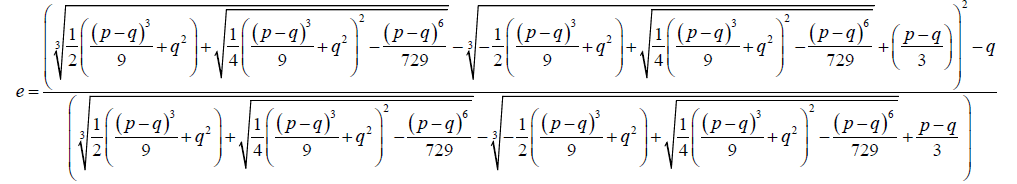 (28)
(28)
From 20:
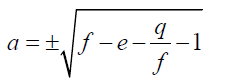 (29)
(29)
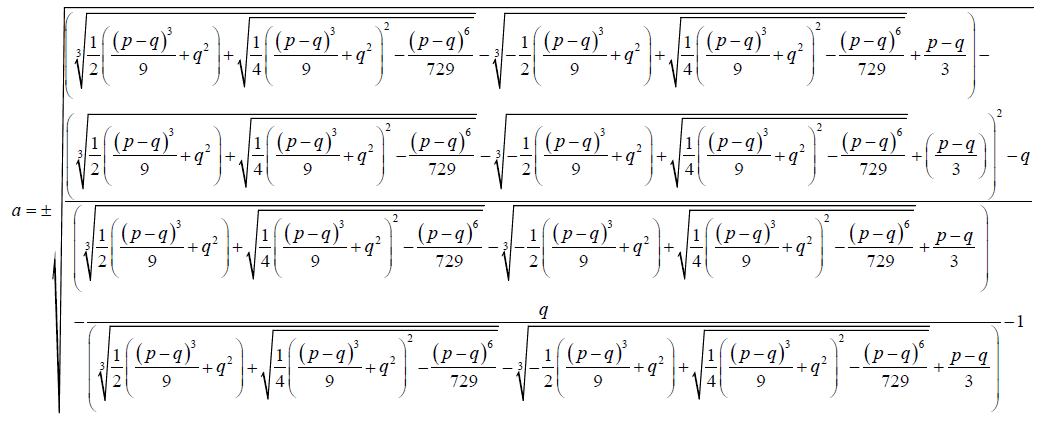 (30)
(30)
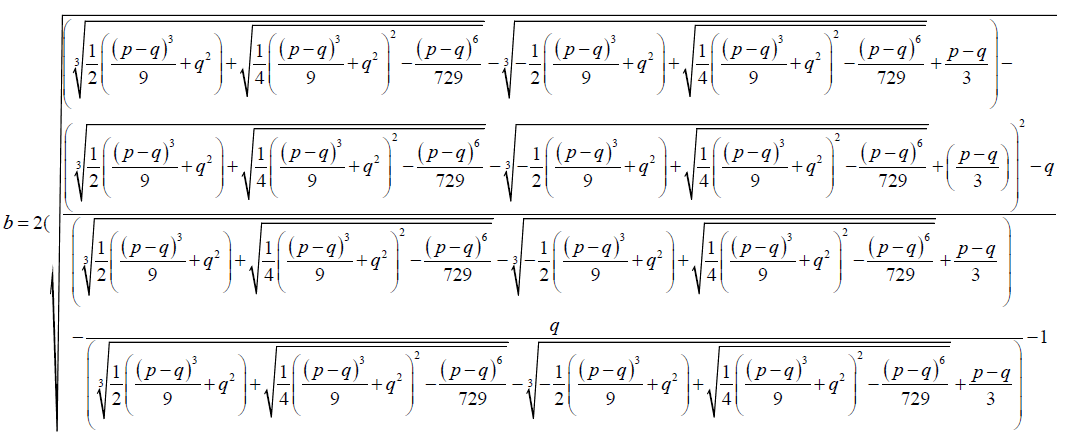 (31)
(31)
Consider one of the auxiliary cubic equations of the trinomial sextic equation above:
x3 + x2 + ex + f = 0 (32)
The first root of the sextic equation is given by:
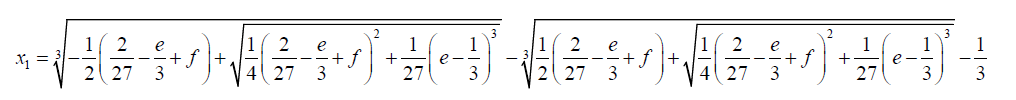 (33)
(33)
If we write the equation 20 in the form below:
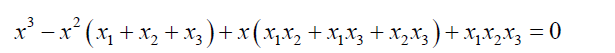
Then x1 + x2 + x3= −1 (34)
x1 x2 + x1 x3 + x2 x3 = e (35)
x1 x2 x3 = f (36)
From 32 and 33 we obtain the quadratic equations below:
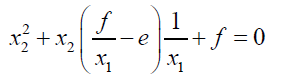 (37)
(37)
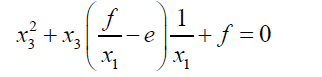 (38)
(38)
If:
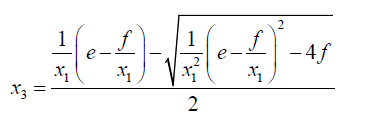 (39)
(39)
Then:
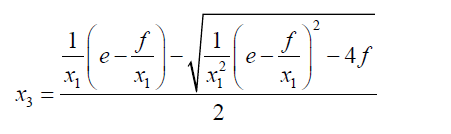 (40)
(40)
Consider the next auxiliary cubic equation:
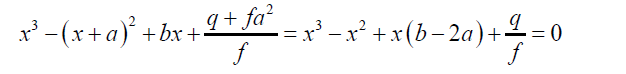 (41)
(41)
One of its roots is given by:
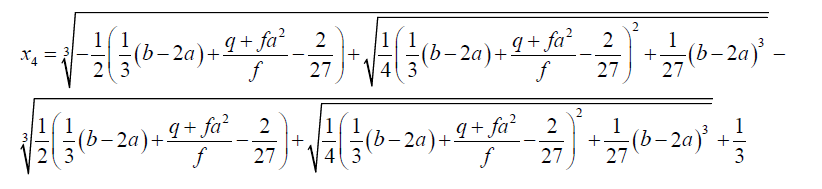 (42)
(42)
If we write the equation 39 in the form below:
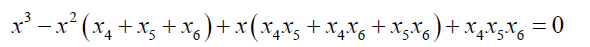 (43)
(43)
Then x5 + x6 + x7 =1 (44)
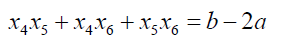 (45)
(45)
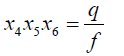 (46)
(46)
From 43 and 42 we obtain the following quadratic equations:
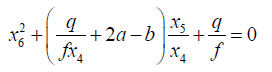 (47)
(47)
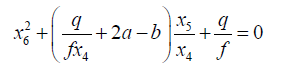 (48)
(48)
If:
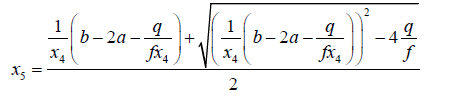 (49)
(49)
Then:
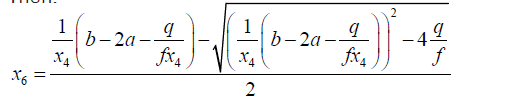 (50)
(50)
The equation 30 can be converted to sixth root by changing to algebraic form of order 6.
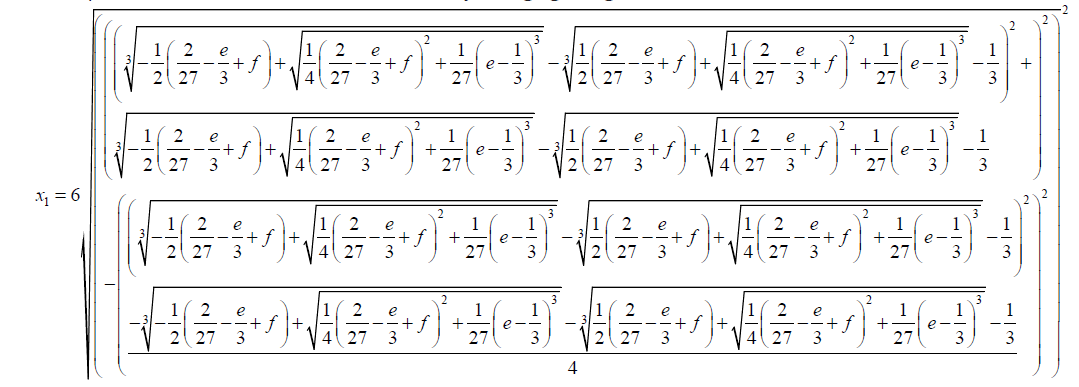 (51)
(51)
A formula for the trinomial sextic equation has been achieved. Algebraic solutions of higher degree polynomials are achievable. Galois groups of higher degree polynomials are solvable. Numbers can be expressed in algebraic form to the order n. The factorization approach is a possible candidate method for solving higher degree polynomial equations.