ISSN: 2320-2459
ISSN: 2320-2459
Independent Researcher, PhD in Mechanical Engineering, Italy
Received date: 10/02/2016; Accepted date: 10/03/2016; Published date: 30/03/2016
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
The main purpose of this paper lies in the attempt to identify a different meaning concerning equations usually classified as relativistic, such as the well known Lorentz Transformations. On the one hand, we can no longer deny that several phenomena can be effectively described by the above-mentioned equations; on the other hand, generally speaking, we should acknowledge that, although some mathematical relations have proved to be evidently suitable for describing the phenomenological reality, their meaning could be deeply different from the one we are used to ascribing to them. The current cosmological theories contemplate the possibility that our Universe could be characterized by a positive curvature. In this case, with the usual hypothesis of homogeneity and isotropy, our Universe is commonly imagined as evenly spread on the surface of a four dimensional ball. In this paper, the existence of at least a further spatial dimension is at least contemplated: in other terms, from a topological point of view, the Universe is no longer assimilated to a three dimensional spherical shell, but rather to a closed 4 - ball. As a consequence, the concept of material point should be replaced by the one of material segment. The angular distance between two points is equal to the angle formed by their radial extensions; the geodesic distance depends on the value of the speed. Naturally, the speed of light is still to be considered constant and independent of the motion of the source. Time is considered absolute. Among the various results, the possibility of travelling apparently faster than light stands out.
Metric expansion, Extra dimensions, Lorentz transformations, Relativistic energy, Faster than light.
Let's consider a uniform circular motion. The speed is constant and equal to c. Referring to Figure 1, with obvious meaning of symbols and signs, the following relations can be easily obtained:
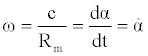 (1)
(1)
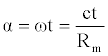 (2)
(2)
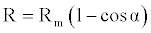 (3)
(3)
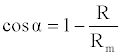 (4)
(4)
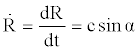 (5)
(5)
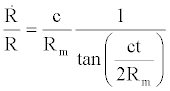 (6)
(6)
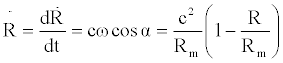 (7)
(7)
If we consider a material point whose motion is defined by relation (3) (in other terms, a simple harmonic oscillator consisting of a mass and an ideal spring), the elastic constant can be written as follows:
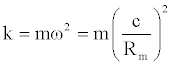 (8)
(8)
As a consequence, the total mechanical energy acquires the following form:
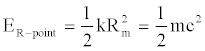 (9)
(9)
Now, we can exclusively modify the amplitude (A) of the motion, keeping the values of mass and pulsation constant, so obtaining:
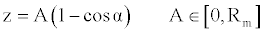 (10)
(10)
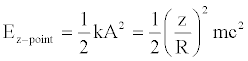 (11)
(11)
The material point can be replaced by a material segment characterized by the same mass (in other terms, the spring is no longer considered as ideal). The length (R) of the segment evolves in accordance with relation (3). We can define the linear density as follows:
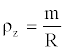 (12)
(12)
In regard to the mass of an infinitesimal portion of the above-mentioned segment, we can state the following:
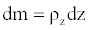 (13)
(13)
The mass of a portion of segment, characterized by a length equal to z, can be easily evaluated as follows:
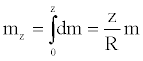 (14)
(14)
The energy related to an infinitesimal material segment can be written as follows:
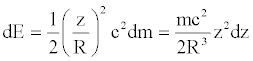 (15)
(15)
Therefore, the final expression for the energy of a material segment, whose length is equal to z, acquires the underlying form:
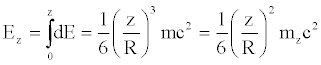 (16)
(16)
Let's consider a 4 - ball, centered at the origin, whose radius is equal to R. We know that the corresponding boundary is a three dimensional surface (a hypersphere) characterized by the following identity:
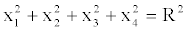 (17)
(17)
Let’s suppose that the mass of our Universe is evenly spread on the surface described by the previous identity [1]. Moreover, let’s suppose that the radius (R) could evolve in accordance to relation (3). The variation of the radius of curvature and, as a consequence, the variations of distances have to be considered as exclusively metric. The so called Hubble parameter [2] is provided by relation (6). Basically, taking into account relation (7), we suppose that our Universe is cyclic [3] and characterized by four consecutive phases: an accelerated expansion, a decelerated expansion, a decelerated contraction, an accelerated contraction. All the above-mentioned phases have the same duration.
Now, we can consider the following material point
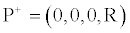 (18)
(18)
and its antipode (the one diametrically opposite)
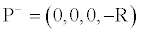 (19)
(19)
According to the identity in (17), if we set
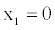 (20)
(20)
we obtain a sphere characterized by the following identity:
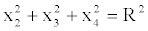 (21)
(21)
As a consequence, in this three-dimensional scenario, we can consider the point
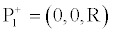 (22)
(22)
and its antipode
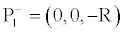 (23)
(23)
By repeating the procedure for x2 and x3 (setting equal to zero, one at a time, x2 and x3), we can synthetically write:
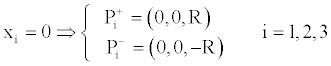 (24)
(24)
Basically, our analysis will be carried out by considering the intersections between the 4 - ball, whose boundary is defined by relation (17), and the hyperplanes defined by the identity
 (25)
(25)
Now, we have to replace the points previously considered with line segments bordered by the center. Each line segment could be intuitively provided with an orientation. For reasons that will be later discussed, the segments have to be considered half-open, since the center of the ball cannot be properly included.
In accordance to relation (16), with obvious meaning of notation, the energy related to a portion of material segment, characterized by a length (z) less than or equal to the radius of the ball, can be written as follows:
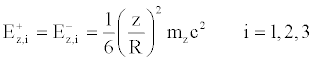 (26)
(26)
Therefore, for a whole segment we can state the following:
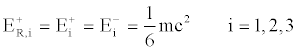 (27)
(27)
Now, we have to suppose that each material point and its antipode are actually the same thing. Moreover, as previously stated, each point has to be considered as an end of a segment bordered, on the other side, by the center of the ball. As a consequence, for each of the three dimensional scenarios that arise from the identity in (25), the energy that can be ascribed to a material point can be written as follows:
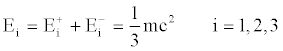 (28)
(28)
Finally, by superposition, we can easily obtain the total amount of mechanical energy related to what we are used to defining and perceiving as a material point:
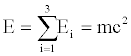 (29)
(29)
From this moment onwards, coherently with our perception of reality, we will exclusively speak in terms of material point. It is fundamental to underline that, in this context, the gravitational effects will be ignored. More precisely, each point is considered as provided with a mass whose value is not sufficient to produce spatial deformations.
Let’s suppose that each material point at rest is provided with an energy whose value is established in accordance to relation (29), commonly called mass-energy equivalence [4]. In addition to this, we have to hypothesize that the energy must remain the same, whatever may happen.
Taking into account the relations (14) and (29), if a material point starts moving with a constant tangential speed equal to v, the conservation of energy may be written as follows:
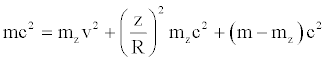 (30)
(30)
The motion would produce a mass reduction we cannot perceive, since the linear density remains the same. Let's focus on the second member of the previous identity. The first addend represents the kinetic energy; the second represents an energy that we could define as potential (related to the level at which the motion takes place); the third is equal to the energetic difference between the two configurations (at rest and in motion).
From relation (30) we can immediately obtain:
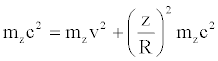 (31)
(31)
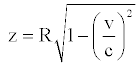 (32)
(32)
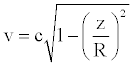 (33)
(33)
Relation (32) can be interpreted as follows: if a point starts moving with a speed equal to v, it is dragged, if we can say so, towards an inner level (or surface). The level reached is characterized by a radius of curvature equal to z. The final radial extension is equal to the radius of curvature (z): in other terms, the segment undergoes a contraction.
If we use the well known position for the so called Lorentz (or relativistic) factor [5]
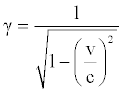 (34)
(34)
we can write the third addend at the second member of equation (30) in the following way:
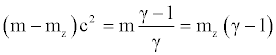 (35)
(35)
Obviously, the domain of the relativistic factor does not include a value of v equal to c. As a consequence, a material point can never actually travel at the speed of light. Alternatively, the contraction due to the motion can never be so extreme as to reduce the radial extension of a point to zero. For this reason, as revealed in advance, the segments have to be considered as half-open.
We can write relation (31) using the position in (34) so obtaining:
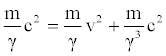 (36)
(36)
By multiplying the first and second member of equation (36) by the relativist factor, we immediately obtain:
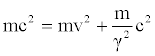 (37)
(37)
The first member of the previous equation should represent the so called relativistic energy.
From relations (14) and (37), making explicit the relativistic factor, we finally obtain:
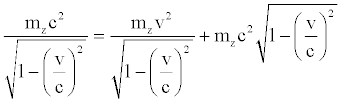 (38)
(38)
If we use the following positions
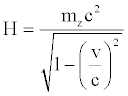 (39)
(39)
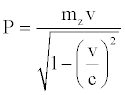 (40)
(40)
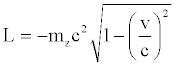 (41)
(41)
we can write:
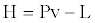 (42)
(42)
H represents the Hamiltonian, P the momentum, L the Lagrangian. From relation (38) it is easy to deduce:
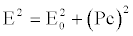 (43)
(43)
If we change notation, using E for the Hamiltonian and E0 for the energy usually defined at rest (EZ), we can immediately write:
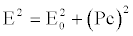 (44)
(44)
If we replace mz with m0, so introducing the concept, by the time abandoned, of relativistic mass
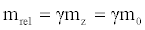 (45)
(45)
we can write relations (37) and (38) in the following way:
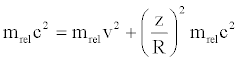 (46)
(46)
Obviously, the relations (31) and (46) are characterized by the same form.
Let’s consider now two points at rest, placed in O and P. As previously stated, if the point initially placed in O starts moving with a constant speed equal to v, it is dragged towards an inner level characterized by a radius of curvature equal to z. As a consequence, the arc length between O and P undergoes a contraction. Referring to Figure 2, with obvious meaning of notation, we can easily write as follows:
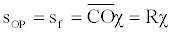 (47)
(47)
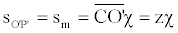 (48)
(48)
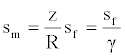 (49)
(49)
The speed, the real one, has to be thought of as the ratio between the reduced distance (the arc length) and the time elapsed to cover it. Time is considered absolute. In other terms, we have:
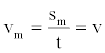 (50)
(50)
An observer at rest (placed on the external surface, characterized by a radius of curvature equal to R) will measure a speed greater than v. In fact, although the time elapsed is exactly the same, the space covered, from the observer's point of view, is greater. As a consequence, we can define a virtual speed as follows:
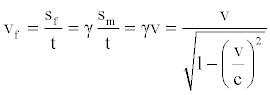 (51)
(51)
It’s easy to deduce that, if the real speed tends to c, the virtual one tends to infinity.
Once again, let's suppose that a material point, initially placed in O, starts moving with a constant speed equal to v. Moreover, let's suppose that, simultaneously, another point, placed in P, sends a light signal. Actually, according to what previously exposed, the signal is sent from each of the points of the radial extension of P. Obviously, the signal is propagated along each tangential direction and its speed is equal to c (the speed does not depend on the possible motion of the source). The motion, as we perceive it, takes place on a surface characterized by a radius of curvature (z) whose value depends on the speed of the point. As a consequence, as soon as the motion starts, the distance between the point and the source undergoes a contraction. More precisely, the contracted distance is equal to the arc bordered by O' and P'.
Referring to Figure 3, we can write as follows:
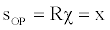 (52)
(52)
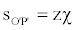 (53)
(53)
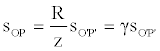 (54)
(54)
Let's suppose that the point sees the signal after a time t' (E’ is the meeting point). If we denote with x' the coordinate of the source at the time t', with respect to the mobile reference frame, we can write:
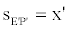 (55)
(55)
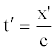 (56)
(56)
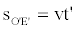 (57)
(57)
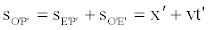 (58)
(58)
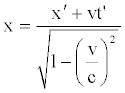 (59)
(59)
The previous relation represents the first Lorentz transformation.
If we divide the first and second member of the relation (59) by c, we obtain:
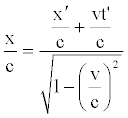 (60)
(60)
Taking into account relation (56) we can write relation (60) as follows:
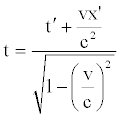 (61)
(61)
The previous relation represents the second Lorentz transformation.
Since we have supposed a merely metric variation of distances (the space may be imagined as some sort of elastic tissue), the meaning of equation (61) becomes extremely banal. Very simply, bearing in mind that time is supposed as being absolute, if the moving point intercepts the signal at the time t' (when the coordinate of the source, with respect to the mobile reference frame, is necessarily equal to x'), an observer at rest, placed in O, will see the signal at the time t.
The inverse transformations can be easily obtained by supposing that the same point starts moving along the opposite direction with a constant speed equal to v. Once written the transformations, in order to obtain the final form, we have to switch the superscripts. The reason is very simple: this time, we have to consider as mobile the reference frame (or the observer) actually at rest, since it seems to be approaching the source.
The results above exposed are obviously characterized by several approximations: after all, the title itself should convey the idea of an exclusively introductive work. Furthermore, although it would have been possible to obtain the same results by following a different line of reasoning (using the concepts of surface tension and hydrostatic pressure, so as to define a stress-energy tensor), a more intuitive approach has been evidently preferred. Time is considered absolute. The speed of light is still considered constant and independent of the motion of the source. Space could be meant as radiation at rest. We have supposed the subsistence of an extra spatial dimension, so as to modify the concept of material point. More precisely, the concept of material point has been replaced by the one of material segment. In other terms, we have imagined the existence of something that could exceed our perception. Each material point is conceived as provided with an energy whose value is still established in accordance to the well known mass-energy equivalence. The above-mentioned value is compatible with several configurations, characterized by different values of speed and mass. As soon as a material point starts moving, it is as dragged towards a level characterized by a lower energy, so as to keep the total energy constant. Distances and dimensions undergo a contraction. In particular, the distance between two points, meant as the arc of circumference bordered by the considered points, depends on the value of the speed. The mass undergoes a reduction we cannot perceive, since the linear density remains the same: as a consequence, a new kind of energy has to be considered. The new term, usually identified with the kinetic energy, represents the energetic difference between the two configurations (at rest and in motion). In some way, this energy is related to the preservation of the spatial lattice integrity. If we had considered gravitational effects, in fact, the energy in question would have been related to the preservation of the spatial deformation induced by the mass. During motion, there's no mass on the external surface since the material segment has undergone a radial contraction. As a consequence, in case of gravitational effects, what we have defined as virtual speed has to be exclusively ascribed to the motion of the spatial deformation due to the mass. The real velocity can never equate the speed of light. On the contrary, the virtual speed can tend to infinity. As we know, in fact, if it is true that a material point cannot travel faster than light, it is also true that the space on the contrary can.