A Commentary on the Analogy between Stochastic Electrodynamics and Nonrelativistic Quantum Electrodynamics

About the Study

Stochastic Electro Dynamics (SED) is a theory that studies the motion of charged particles according to Classical Electro Dynamics (CED), but departs from standard CED by the assumption that there is a Random Electromagnetic Radiation (RR) filling space. In SED charged particles may achieve a state of dynamical equilibrium because they may radiate but also absorb energy from the RR. Thus matter (e.g. atoms) may be stable at a difference with pure CED.

RR may be studied expanding it in plane waves with complex amplitudes {a₁}.

Assuming statistical independence of the amplitudes and maximal information entropy, we get the probability distribution.

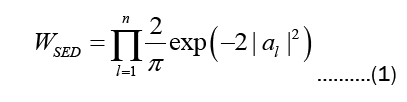
In free space it is plausible that the spectral energy density, S (ω), (i.e. energy per unit volume and unit frequency interval) of RR is homogeneous, isotropic and Lorentz invariant. This determines S (ω) modulo a parameter that we identify with Planck constant, ħ. That is S (ω) ∝ ω3 leading to a mean energy per mode of RR

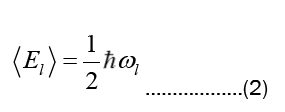
Equations (1) and (2) plus Maxwell-Lorentz electrodynamics fully define SED.

The study of physical systems within SED leads to predictions in agreement with non-relativistic Quantum Mechanics (QM) for linear systems, like systems of harmonic oscillators. This provides an intuitive explanation of several phenomena taken as purely quantum, e.g. the Debye theory for the specific heats of solids, the Unruh effect, the Casimir effect and London-vander Waals forces. However the predictions of SED for nonlineaer systems, e.g. the hydrogen atom, disagree with those of quantum theory and experiments.

Non-Relativistic Quantum Electro Dynamics (NRQED) is defined as QM coupled to the quantized radiation field. It is studied usually within the Hilbert Space formalism (HS), but an equivalent approach is the Weyl-Wigner theory (WW). It is possible to pass from HS to WW via the Weyl transform which, applied to the electromagnetic field, associates complex amplitudes 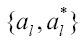to the usual annihilation and creation operators 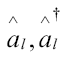The states and observables in HS become functions of the amplitudes 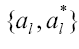in WW. In particular the function associated to a state is named its Wigner function. It is remarkable that the Wigner function of the vacuum state is equation (1), which in NRQED appears as just a mathematical function. In sharp contrast in SED equation (1) is interpreted as a probability distribution.

In the standard quantum theory of the field (formulated in HS) it is assumed that the vacuum state has zero energy, although there are vacuum fluctuations known as “Zero Point Field” (ZPF). There may be also excited states with positive energy got from the application of creation operators to the vacuum state. Thus the excited states of the quantized electromagnetic field are assumed to consist of either a definite number n of particles, named photons, or linear combinations of several photon states.

This interpretation of the standard HS formulation of the quantized field might be translated to the WW formalism. However the WW suggests a different interpretation close to SED. In fact the plausible picture of the “vacuum state” represented by equation (1) in WW is a RR that possesses a large 2 energy, see equation (2), and the excited states should correspond to addition of some radiation to the RR. Also the evolution of the quantized field in WW is just given by classical Maxwell-Lorentz theory.

The summary between SED and NRQED there are analogies, but also differences. The latter are:

1) NRQED in the standard Hilbert space formalism does not provide a simple realistic interpretation, while SED is a classical theory where the picture of reality is obvious.

2) The set of states in SED does not agree with the set of states in NRQED because SED requires positivity of the (probability) distribution of modes for any state, but the Wigner function in NRQED is not always positive.

3) For nonlinear systems the Planck constant, h, appears in NRQED both in the Hamiltonian of the quantized field and also in the particles Hamiltonian. However it appears only once in SED, that is in the RR equation (2), because the equations of motion of charged particles are assumed to be those of CED.