A Theoretical Calculation of Zero-Field Splitting Parameter for Mn2+ Ion in Cadmium Ammonium Phosphate Hexahydrate

Abstract

The crystal field parameters (CFP) and zero-field splitting (ZFS) parameter D of Mn2+ ion at axial symmetry site in cadmium ammonium phosphate hexahydrate (CAPH) single crystal are modeled. The calculation is carried out with the help of superposition model and the perturbation formulae. The theoretical ZFS parameter D is in good agreement with the experimental value. The theoretical modeling supports the conclusion drawn from experimental study that Mn2+ ion occupies substitutional site in CAPH. Ignoring local distortion, the value of D comes out as 306.1×10-4 cm-1; while considering small local distortion, the value of D is obtained as 308.4 ×10-4 cm-1. The experimental value of D is 305.5×10-4 cm-1.

Keywords

Organic crystal, Crystal structure, Symmetry, Crystal fields, Spin-orbit effects, Electron paramagnetic resonance.

Introduction

Electron paramagnetic resonance (EPR) studies yielding zero-field splitting (ZFS) parameters are important for the analysis of structural distortions and local site symmetry around the transition metal ions in crystals [1-7]. The microscopic spin-Hamiltonian (MSH) theory is widely used for the analysis of EPR spectra of transition metal ions. The spin Hamiltonian (SH) data from EPR spectra are correlated with optical spectroscopy and structural data with the help of MSH theory. Experimental and theoretical study indicated that the spin Hamiltonian parameters for transition metal (d⁵ (⁶S)) ions in crystals are affected very sensitively by the local structure. Consequently the SH theory has been extensively used in various types of crystal lattices.

The crystal-field parameters are evaluated by means of superposition model [8,9]. The ZFS parameters are determined through the electrostatic, the spin-orbit coupling, and the crystal-field parameters of the d5 ion in a crystal [10]. Out of iron group transition metal ions, Mn²⁺ is important for the reason that its ground state is ⁶S_5/2 [11-15]. The electron spin is affected by high order interaction of crystalline electric field, and in the presence of external magnetic field orientation of spins become free [16]. The spin–lattice relaxation time is large for S state ions, due to which Mn²⁺ shows fine EPR spectra [2,15,17,18] at RT.

In this paper, the superposition model is used to obtain crystal field (CF) parameters and MSH theory together with CF parameters is used to predict the ZFS parameters for Mn²⁺ ions at the substitutional sites in cadmium ammonium phosphate hexahydrate (CAPH) crystal at room temperature (RT).

Crystal Structure

The crystal structure of CAPH is analogous to the naturally occurring biomineral struvite [19]. This crystal belongs to orthorhombic system having space group Pmn2₁, The unit cell dimensions are a = 6.941(2) Ǻ, b = 6.137(2) Ǻ and c = 11.199(4) Ǻ [20], and there exist two molecules per unit cell (Z = 2). Six water molecules form a distorted octahedral environment around the cadmium atom. The bond length of Cd-O lies within the range from 2.046 to 2.1076 Ǻ.

The Mn²⁺ ion in CAPH crystal substitutes at Cd²⁺ site [21]. The phenomenological SH of 3d5 ion configuration for tetragonal symmetry crystal field can be written as [2,22,23]

H=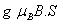

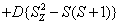
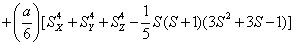
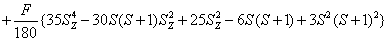
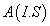+ (1)

where the first term represents electronic Zeeman energy in which B is the external field, g is the spectroscopic splitting factor and μ_B is Bohr magneton. The second, third, and fourth terms are the second order axial, fourth-rank cubic and fourthrank axial ZFS terms [2]. The fifth term is the hyperfine interaction term. S, D, a, F represent the effective spin vector, second order axial, fourth-rank cubic and fourth-rank axial ZFS parameters, respectively. For the electronic Zeeman interaction isotropic approximation is used and usually it is valid for Mn²⁺ ions [2,24]. From the EPR spectra the direction of the maximum overall splitting is taken as the z axis and the direction of minimum splitting as the x axis [25]. The laboratory axis system (x, y, z) corresponds to the crystallographic axis system (CAS). The Z- axis of the local site symmetry axis i.e. the symmetry adopted axis (SAA) is along the metal-oxygen bond and the rest two axes X, Y are perpendicular to this.

The Hamiltonian for a d5 ion can be written as

H = H₀+ H_cf + H_{so (2)}

in which H_cf=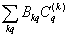

shows the crystal field Hamiltonian. H₀ and H_so are free ion Hamiltonian and spin-orbit (SO) coupling, respectively. Because of spin-spin coupling being very small [26-28], its contribution has not been considered in Eq. (2). The total crystal field of SO interaction is taken as perturbation term [29,30]. The calculation in the strong-field scheme is formulated by Macfarlane for F-state ions [31]. In CAPH crystal, oxygen atoms form a distorted octahedron around the Cd atom [20] and yield axial local symmetry. For axial symmetry, the SO contributions to the ZFS parameter D for 3d⁵ ions can be written as [30]

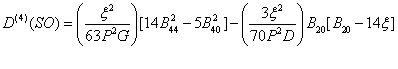(3)

where P = 7(B+C), G = 10B+5C and D = 17B+5C. P, G, and D are the energy separations between the excited quartets and the ground sextet. Racah parameters B and C describe the electron-electron repulsion. In Eq. (3) only fourth order term is considered as other perturbation terms are very small [32]. By considering the average covalency parameter N, the parameter B, C and ξ are specified in terms of N as, B = N⁴B₀, C = N⁴C₀ and ξ = N² ξ₀, where B₀ and C₀ are the Racah parameters and ξ₀ is the spin-orbit coupling parameter, for free ion [33,34]. B0= 960 cm^-1, C₀ = 3325 cm^-1, ξ₀ = 336 cm^-1 [2] are used here.

From optical study of Mn²⁺ doped zinc ammonium phosphate (ZAPH) [35], B = 917 cm^-1 and C = 2254 cm^-1. As CAPH is isomorphous to ZAPH [35]; B, C and Dq are taken from this paper. By using these data in Eq. (4) [36] below,

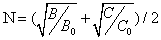(4)

N can be obtained.

By applying the superposition model the crystal-field parameters for Mn²⁺ doped CAPH single crystal are calculated and using these parameters in Eq. (3) ZFS parameter D is determined. Similar approach has been used by several earlier workers [37] for estimating ZFS parameters.

Superposition Model

The superposition model is effectively used for explaining the crystal-field splitting. In recent times, this model is frequently applied for 3dn ions [8,32]. With the help of this model the crystal field parameters can be determined by the equations [38]

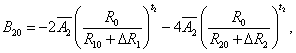5(i)

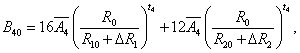5(ii)

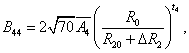5(iii)

where R₀ is the reference distance. In general, it is chosen as the mean value of all six bond lengths (for axial symmetry). The mean value of two out of six Cd-O bond lengths are indicated by R₁₀ and the mean value of remaining four bond lengths are indicated by R₂₀, further ΔR₁ and ΔR₂ indicate the distortion parameters. Ā_k and t_k are the intrinsic parameter and power law exponent, respectively [39,40].

For 6-fold cubic coordination 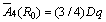[10]. For 3d⁵ ions, 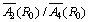lies in the range 8-12 [32,40]. Using Dq= 756 cm^-1 [35], 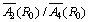can be determined taking the value of ratio 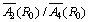. The power law exponent in the case of Mn²⁺ ion is adopted as t₂ = 3, t₄ = 7 [41]. For the intrinsic parameter values for the superposition model semi-ab initio calculations are done for other transition metal ions [42].

Results and Discussion

In the present study the bond length of six ligands R_j (Figure 1) is calculated as given in Table 1. The value of B and C are taken from the optical study [35] as 917 and 2254 cm^-1, respectively. First of all ignoring the local distortion the value of D is calculated. For this, taking 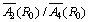= 8 and reference distance R₀ = 0.28 nm, which is the mean value of six ligands distance, the value of D comes out to be D = 87342×10^-4 cm^-1. From EPR study, the experimental value is given as D = 305.5×10^- 4 cm^-1 [20]. Here it is seen that the theoretical value is very high. Now, if the ratio 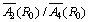is changed to 12, then D = 79282×10^-4 cm^-1, which is again high. Further, using the same ratio and R₀ = 0.212 nm, which is the sum of ionic radii of Mn²⁺ = 0.08 nm and O^2- = 0.132 nm, the result comes out as D = 1103 ×10^-4 cm^-1, which is also very large. If 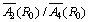= 8 is taken, then D becomes 467.4×10^-4 cm^-1, which is again large. Now by taking R₀ = 0.210 nm, the value comes out as D = 306.1×10^-4 cm^-1, which is in reasonable agreement with the experimental value D = 305.5×10^-4 cm^-1.

Figure 1: Coordination about Mn²⁺ ion in CAPH.

Table 1: Metal-oxygen bond distances R_j for Mn²⁺ ion in cadmium ammonium phosphate hexahydrate single crystal.

Further, considering local distortions as ΔR₁ = -0.0008 nm and ΔR₂ = -0.0009 nm, reference distance R₀ = 0.28 nm (the mean value of six ligands distance) and ratio 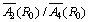= 8, the value of D comes out to be 62759.9×10^-4 cm^-1. It is noticed that the theoretical value is very high. Again taking the same value of R₀ (0.28 nm) but changed value of the ratio, 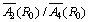= 12, the value of D comes out as 55681.7 ×10^-4 cm^-1, which is also larger than the experimental value. Further, using the same ratio but R₀ = 0.212 nm, which is the sum of ionic radii of Mn²⁺ = 0.08 nm and O2- = 0.132 nm, the result comes out as D = 1289.8 ×10^-4, which is again very high and if 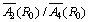= 8 is taken with the same R₀ = 0.212 nm, the result comes out as D = 37.0×10^-4 cm^-1, which is very low as compared to experimental value. At R₀ = 0.166 nm, the value of D comes out as 308.4 ×10^-4 cm^-1, which is in reasonable agreement with the experimental result D = 305.5×10^-4 cm^-1 .

By using Eq. 5(i) - 5(iii), crystal-field parameters B_kq are obtained as: B₂₀ = -19896 cm^-1, B₄₀ = 7468.1 cm^-1, B₄₄ = 10325.1 cm^-1 when distortion parameters ΔR₁ and ΔR₂ are not considered in the calculation. Considering ΔR₁ = -0.008 Ǻ and ΔR₂ =-0.009 Ǻ, the B_kq parameters are: B₂₀ = -9484 cm^-1, B₄₀ = 1329.8 cm^-1, B₄₄ = 1839.6 cm^-1. The above theoretical investigation suggests that Mn²⁺ ion enters the host lattice substitutionally in CAPH. This supports the conclusion drawn by EPR study.

Conclusion

Zero-field splitting parameter D for Mn²⁺ doped CAPH in axial symmetry has been calculated with the help of superposition model and perturbation formulae. The theoretical value of D is in reasonable agreement with the experimental value. This analysis indicates that Mn²⁺ ion enters the host lattice substitutionally, which supports the experimental result obtained by EPR.

Acknowledgement

The authors are thankful to the Head, Department of Physics, University of Allahabad, Allahabad for providing departmental facilities.

References

1. Altshuler S and Kozyrev BM. Electron Paramagnetic Resonance in Compounds ofTransition Elements, Wiley, New York, 1974.
2. Abragam A andBleaney B. Electron Paramagnetic Resonance of Transition Ions. Dover, New York, 1986.
3. Pilbrow JR. Transition Ion Electron Paramagnetic Resonance, Clarendon Press,Oxford, 1990.
4. Mabbs FE and Collison D. Electron Paramagnetic Resonance of d Transition-MetalCompounds, Elsevier, Amsterdam, 1992.
5. Spaeth JM et al. Structural Analysis of Point Defects inSolids, Springer Series in Solid-State Sciences. 1992; 43.
6. Rudowicz C. Magnetic Resonance. Rev. 1987; 13: 1-89.
7. C. Rudowicz, S. K. Misra, Appl. Spectrosc. Rev. 36 (2001) 11-63.
8. YeungYY and Newman DJ.Superposition-model analyses for the Cr3+ 4A2 ground state. Phys. Rev. B. 1986;34: 2258-2265.
9. Newman DJ and Ng B.The superposition model of crystal fields. Rep. Prog. Phys. 1989; 52: 699-763.
10. Yu WL and Zhao MG.Phys. Rev. B. 1988; 37: 9254-9267.
11. Mishra SK. Handbook of ESReds. Poole CP and Farach HA. Springer, New York, 1999;IX: 291.
12. Anandlakshmi H et al.Single crystal EPR studies of Mn(II) doped into zinc ammonium phosphate hexahydrate (ZnNHPO4·6H2O): A case of interstitial site for bio-mineral analogue. Pramana. 2004; 62: 77-86.
13. Rao PS. Spectrochim. Acta A. 1993; 49: 897-901.
14. Mishra SK.Estimation of the Mn²⁺ zero-field splitting parameter from a polycrystalline EPR spectrum. Physica B. 1994; 203: 193-200.         
15. Mc Garvey BR. Electron Spin Resonance of Transition Metal Complexes in: Transition Metal Chemistry.ed. R. L. Carlin, Marcel Dekker, New York. 1966; 3.
16. NatarajanS and MohanaJKR.Curr. Sci. 1976; 45: 490-491.
17. Kuska HA et al. Interscience. New York. 1968.
18. Anthonisamy VSX et al. Spin-lattice relaxation of Co(II) in hexaaquocobalt(II) picrylsulphonatetetrahydrate: An estimate from EPR line width of the dopant, Mn(II). Physica B. 1999; 262: 13-19.
19. Ravikumar RVSSN et al.Spectroscopic investigations on vanadyl doped cadmium struvite. PhysicaScr. 1997; 55: 637-638.
20. Whitaker and Jeffery JW.The crystal structure of struvite, MgNH4PO4.6H2O.ActaCryst. B. 1970; 26: 1429-1440.
21. Shiyamala C et al.Single Crystal EPR Study of Mn(II)-Doped Biomineral: Cadmium Ammonium Phosphate Hexahydrate. Physica Scr. 2002; 66: 183-186.
22. Abragam A and Pryce MHL.Theory of the Nuclear Hyperfine Structure of Paramagnetic Resonance Spectra in Crystals. Proc. Roy. Soc. 1951; 205: 135-153.
23. Bleaney B and Stevens KWH.Rep. Prog. Phys. 1953; 16: 108-159.
24. Weil JA and Bolton JR. Electron Paramagnetic Resonance: Elementary Theory and Practical Applications. 2nd edn. Wiley, New York, 2007.
25. Rudowicz C and Bramley R.J. Chem. Phys. 1985; 83: 5192-5197.
26. Yang ZY et al. Theoretical investigations of the microscopic spin Hamiltonian parameters including the spin–spin and spin–other-orbit interactions for Ni2+(3d8) ions in trigonal crystal fields. J. Phys.Condens. Matter.2004; 16: 3481-3494.
27. Sharma RR et al. Phys. Rev. 1966; 149: 257-269.
28. Sharma RR et al. Phys. Rev. 1967; 171: 378-388.
29. Watanabe H.Prog. Theor. Phys. 1957; 18: 405-420.
30. Yu WL and Zhao MG. J. Phys. C. 1984; 17: L525-527.
31. Macfarlane RM.J. Chem. Phys. 47 (1967) 2066-2073.
32. Shen GY and Zhao MG.Gauge invariance and fractional quantum Hall effect.Phys. Rev. B. 1984; 30: 3691-3703.
33. Zhao MG et al. A theoretical analysis of zero-field splitting parameters of Mn²⁺ in zinc lactate trihydrate. J. Phys. C:Solid State Phys. 1985; 18: 3241-3248.
34. Jorgensen CK. Modern Aspects of Ligand Field Theory, Amsterdam, North-Holland,1971; 305.
35. Kripal R et al. EPR and optical absorption study of Mn²⁺-doped zinc ammonium phosphate hexahydrate single crystals. Physica B. 2007; 392: 92-98.
36. Pandey S and Kripal R. Zero-Field Splitting Parameters of Cr3+ in Lithium Potassium Sulphate at Orthorhombic Symmetry Site.Acta Phys. Polon. A. 2013; 123: 101-105.
37. Yang ZY et al. Spin Hamiltonian and structural disorder analysis for two high temperature Cr3+ defect centers in α-LiIO3 crystals—low symmetry effects. J. Phys. Chem. Solids. 2003; 64: 887-896.
38. Wei Q.Investigations of the Optical and EPR Spectra for Cr3+ Ions in Diammonium Hexaaqua Magnesium Sulphate Single Crystal. Acta Phys.Polon. A. 2010; 118: 670-672.
39. Wei Q. Spin Hamiltonian parameters and structural disorder analysis for Cr3+ ion in YGG crystals.Solid State Commun.2006; 138: 427-429.
40. Rudowicz C.On the derivation of the superposition-model formulae using the transformation relations for the Stevens operators.J. Phys. C: Solids State Phys. 1987; 20: 6033-6037.
41. Yeom TH ety al. A theoretical investigation of the zero-field splitting parameters for an Mn²⁺ centre in a BiVO4 single crystal J. Phys. Condens.Matter.1993; 5: 2017-2024.
42. Brik MG and Yeung YY. Semi-ab initio calculations of superposition model and crystal field parameters for Co2+ ions using the exchange charge model. J. Phys. Chem. Solids. 2008; 69: 2401-2410.