ISSN: 2320-2459
ISSN: 2320-2459
Najmeddin Arab1* and Ernest Nazaryan2
1Department of Material Science, Branch of Saveh, Azad Islamic University, Saveh, Iran.
2Department of Physics, Yerevan State University, Yerevan, Armenia.
Received date: 26/06/2013 Revised date: 02/07/2013 Accepted date: 05/07/2013
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Mathematical description of the processes of sheet metal forming is very complicated process because of varying loading history and complex stress state in each point of material. The parameters for description of metal behaviour by the mathematical models of sheet metal forming are normally taken from a simplest mechanical test such as, for example, uniaxial traction test. Lately some new tests were developed which are closed to reel forming processes. Deep-drawing of a cylindrical cup occupies a particular place between these tests since it allows study the material work hardening, conditions of friction, springback, wrinkling, plastic flow instability, fracture and some others effects at the same time. In this research, deformation process of a thin ring plate with circular hole has been analyzed. By taking into account the thickness variations, and work hardening, the forming of thin ring plate at plane stress condition has been considered. It is shown that the deformation procedure of each point in the blank can be analysis by non-linear vector function of plasticity
Flanging, Sheet Metal Forming , Thin Plates Forming, Deep Drawing
Mathematical description of the processes of sheet metal forming is very complicatedbecause of varying loading history and complex stress state in each point of material. The parameters for behavior law introduced in the mathematical models of sheet metal forming are normally taken from a simplest mechanical test such as, for example, uniaxial traction test. Lately some new tests were developed which are closed to reel forming processes. Deep-drawing of a cylinderical cup occupies a particular place between these tests since it allows to study material hardening, conditions of friction, springback, wrinkling, plastic flow instability, fracture and some others effects at the same time [1,2]. There are two stages of deep-drawing during the first one the blank holder descends on a circular blank with special diameter and thickness and press it with special force, the process of forming takes place at the second stage when the cylindrical punch descends on the blank and draw it in the hole of matrix (figure 1). One can control the metal flow in matrix by modifying the blank-holder force that changes the friction force. Usually the process keeps on up to the moment of full drawing of the cup. But this is not always possible because of the fracture of the cup generally in the zone of cylindrical wall. It is obvious that the force of material resistance to drawing depends on the diameter of the initial blank against the punch diameter (R / R0 ) – for bigger value of this ratio the force of resistance is bigger. Therefore there is a limiting drawing ratio (LDR) for which full cup drawing is still possible. In one of the first analytical models [1] of this process Hill predicted the upper and the lower drawing limits for isotropic non-hardening material ( e= 1.65 and e= 2.72 respectively). Later models [3,4,5,6,7] improved this approach by considering the current geometry of the process (figure 1) in order to determine the strain rate field and then the stress field and the forces. In each of these models some simplifications were applied, in particular, the hypothesis of cup thickness unchanged during all the process. The current geometry of process when the punch has penetrated in matrix at a distance dm is presented in figure 1. Flange has an exterior diameter (changing in the time) equal to 2Rext, and interior diameter (which is unchanged) equal to 2Rint. The radius of matrix and punch rims are rp and rm respectively. Force Fp, with which the punch acts on the blank increase at the beginning of process because of material ardening in flange and it decreases at the end of process as a result of flange reduction (figure 2).
Analysis of flanging process
The present article is devoted to the theoretical analysis of flanging process of circular holes in thin plates taking into account the interconnected change of thickness and deformation hardening (when the known aspects of flanging process are omitted). Let's consider the forming process at flanging circular holes in thin plates, carried out by a punch with a flat end .In this research, it is shown that the initial equations characterize plastic plane stress state, taking place at flanging circular holes in thin plates,
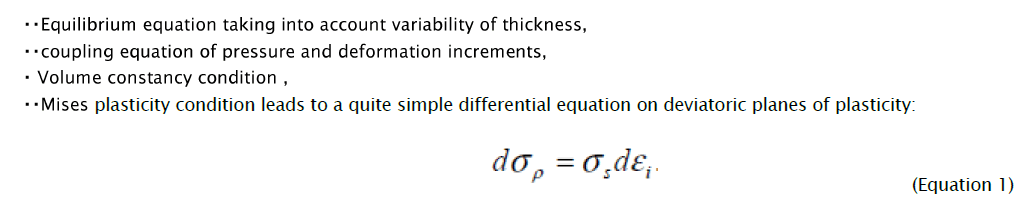
During derivation (1) radial σρ and circumferential σθ pressure, which are expressed through the parameter of the deformed condition, are used in the given way:
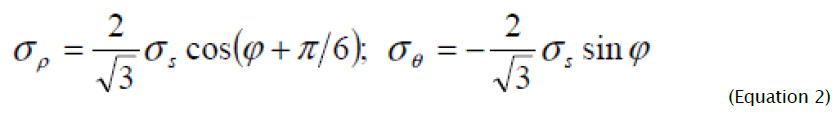
and the components of deformation increments are presented with the help of known equations
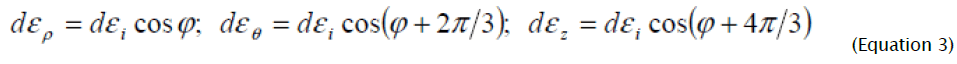
Components of deformation increments (3) unequivocally satisfy intensity of deformation increments, which, taking into account volume constancy condition, is defined by following expression
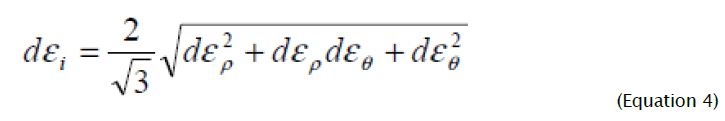
Isotropic deformation hardening is represented on the deviatoric plane of the plasticity cylinder in the form of circles with radiuses σs/√3 which increase in the radial direction by the size determined according to the value of accumulated deformation [9,10]

Where A, n are constants values of deformation hardening. The current value of accumulated deformation, taking into consideration the condition of volume constancy, is defined as:
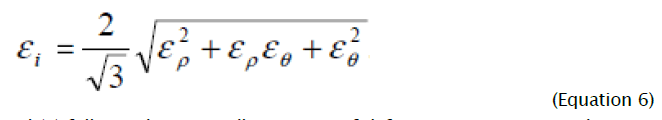
From comparison of equations (4) and (6) follows, that generally intensity of deformation increments dεi is not equal to the intensity increment d εi defined by differentiation of equation (6). Therefore integration of the differential equation (1) taking into account (5) is possible only for the radial ways of deformations at which for the given material element the relation of the deformation increment components remains constant. Parameter φ change limits in the considered problem are determined, based on flanging process definition at which for all deformation site current sizes of circular deformations are positive, increasing from zero on the border of non-deformable part of the blank to the greatest value on the hole edge. From the analysis of equation (2) follows, that on border of not deformable part of blank radial stretching strain cannot exceed the value 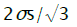 , corresponding to direction
, corresponding to direction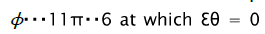 and from the absence condition of radial stretching strain on the hole edge follows that the regional element is deformed under the cnditions of circular stretching in the positive direction of axis ε0 that corresponds to direction
and from the absence condition of radial stretching strain on the hole edge follows that the regional element is deformed under the cnditions of circular stretching in the positive direction of axis ε0 that corresponds to direction 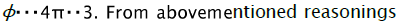 it follows that theoretically possible range of realisation of flanging process, at which
it follows that theoretically possible range of realisation of flanging process, at which 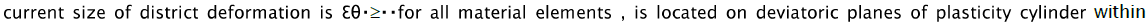 parameter change
parameter change ![]() Hence, all types of deformations in flanging process are completely characterised by the corners occupying a sector with central angle
Hence, all types of deformations in flanging process are completely characterised by the corners occupying a sector with central angle 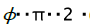 (figure 3).
(figure 3).
If the deformation way coincides with axis εθ - stretching deformation in the circumferential direction, ερ and εz compression deformations numerically equal εθ /2 . If the deformation way coincides with a negative direction of axis εz , then εz compression deformations by thickness, ερ and εθ - the stretching deformations numerically equal εz /2 . If the deformation way coincides with direction ερ = 0, εθ and εz are equal by size and are opposite on sign, pure shift or flat deformation in the plane ( θ , Z ) takes place. If the deformation way coincides with direction εθ = 0 , ερ and εz are equal by size and are opposite on sign, pure shift or flat deformation in the plane ( ρ , Z ) takes place. Thus, ways of deformation with corners 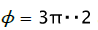 and
and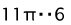 correspond to pure shift, accordingly, in planes ( θ , Z ) and ( ρ , Z ) and with corners
correspond to pure shift, accordingly, in planes ( θ , Z ) and ( ρ , Z ) and with corners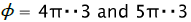 to pure stretchingand compression, accordingly, in circumferential direction and in the direction of thickness. To determine the conformity between coordinates of considered elements and the parameter of the deformed condition we will integrate the equation (1) at earlier accepted assumption about radial character of current deformation accumulation that follows from the assumption about the parity constancy between pressures σρ andσθ
to pure stretchingand compression, accordingly, in circumferential direction and in the direction of thickness. To determine the conformity between coordinates of considered elements and the parameter of the deformed condition we will integrate the equation (1) at earlier accepted assumption about radial character of current deformation accumulation that follows from the assumption about the parity constancy between pressures σρ andσθ
Equating result of integration to the value of radial pressure defined by equation (2) we get
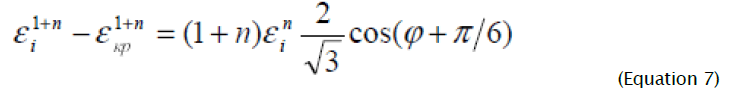
At integration (1) the boundary condition is used, according to which for the boundary element εi = εkp , ερ = 0 (the hole edge is deformed in the circumferential direction in the conditions of linear stretching throughout the whole forming process). The known distribution of deformation intensity by the corner φ allows to determine interrelation between coordinate ρ of the considered element and parameter φ on deviatoric planes of the plasticity cylinder. For the initial stage of forming process
(εkp = 0) having differentiated expression (7) and equated the received result to (3) ( d εi = dεi , dεθ =dρ/ρ) [10], we receive:
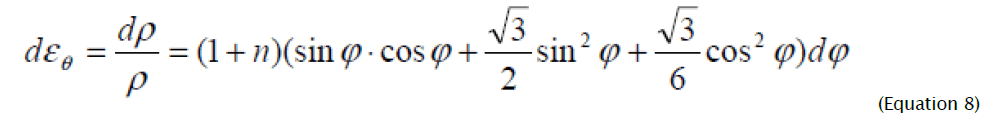
Expression (8) after integration will become:
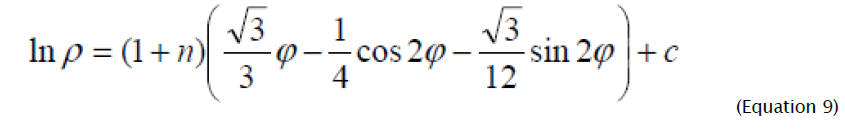
Where the constant of integration c is determined from boundary condition, according to which, at 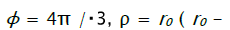 - initial radius of the hole).Substituting the value of integration constant in (9), after simple transformations we will receive:.
- initial radius of the hole).Substituting the value of integration constant in (9), after simple transformations we will receive:.
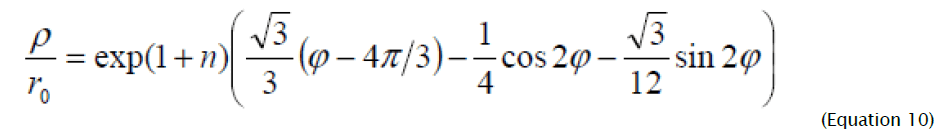
From (10) it follows, that the deformation site has the greatest sizes at 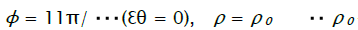 - the radius of die hole) and is equal
- the radius of die hole) and is equal
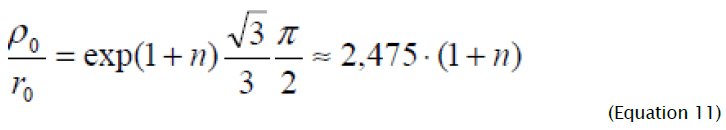
At n = 0 the limiting value of relation ρ 0 / r0 coincides with the result of works [9-11] received when solving the problem taking into account change of thickness for ideally rigid plastic model of deformable material. Equation (10), which establishes unequivocal connection between initial co-ordinate of the considered element and parameter φ, allows to onsider the flanging process dividing it into two stages. At the initial stage of deformation paralel to punch lowering, formation of plastic deformation site from external (on the die hole edge) to the internal border takes place.
Meanwile the blank elements move in radial direction, and their thickness decreases. Hence, there is an element deformed in direction 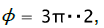 for which radial deformation is ερ = 0 throughout the whole forming process. For definition of coordinate ρ of this element, substituting in (10)
for which radial deformation is ερ = 0 throughout the whole forming process. For definition of coordinate ρ of this element, substituting in (10) 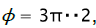 we will receive
we will receive
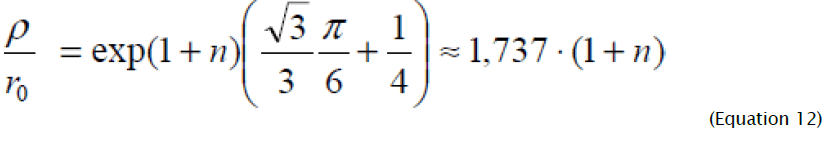
Comparing the received result for the relative co-ordinate, which delimits the shortening area from lengthening in radial direction at n = 0 , with result of work 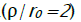 which has been received without taking into consideration the thickness change and the influence of deformation hardening, we see, that in [12] it is a little overrated. Thus, all material elements with the relative coordinate less than the value defined (12), are shortened in radial direction, being exposed to radial compression, and elements with relative coordinate more than this value, are extended in radial direction, being exposed to a radial stretching. Hence, at calculation of parameters of flanging process it is necessary to proceed from the value of flanging coefficient. At small values of deformation flanging coefficient ερ ≤ 0 and the total flange height are less than the width flanging part of blank. At the big values of flanging coefficient when in deformation site ερ changes its sign, compression deformations in radial direction are somewhat compensated by stretching deformations, and it becomes possible to apply the calculation which follows from the equation of length of flange sweep on equatorial line and the width of flanged part of the blank Knowing the character of deformation intensity distribution, it is possible to define deformation components:
which has been received without taking into consideration the thickness change and the influence of deformation hardening, we see, that in [12] it is a little overrated. Thus, all material elements with the relative coordinate less than the value defined (12), are shortened in radial direction, being exposed to radial compression, and elements with relative coordinate more than this value, are extended in radial direction, being exposed to a radial stretching. Hence, at calculation of parameters of flanging process it is necessary to proceed from the value of flanging coefficient. At small values of deformation flanging coefficient ερ ≤ 0 and the total flange height are less than the width flanging part of blank. At the big values of flanging coefficient when in deformation site ερ changes its sign, compression deformations in radial direction are somewhat compensated by stretching deformations, and it becomes possible to apply the calculation which follows from the equation of length of flange sweep on equatorial line and the width of flanged part of the blank Knowing the character of deformation intensity distribution, it is possible to define deformation components:
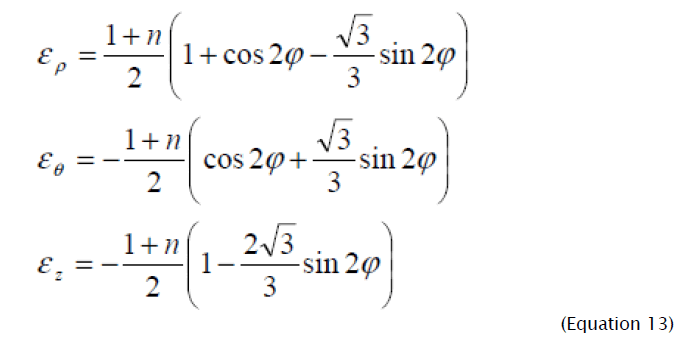
On figure 4 the graphs changes of deformation intensity and deformation components are presented at change of parameter φ in range 4π / 3 ≤ φ ≤ 11π / 6 for the initial stage of deformation (εkp = 0) at n = 0.2. From equations (13) and figure 4 it follows that in the center of deformations some element with parameter of deformed condition φ = 19π /12 at the initial moment of deformation receives the greatest circular deformation equal to √3/3 (1+n). We find the relative coordinate of the material element which has received the greatest circular deformation from (10): ρ/r0 =2.1(1+n).
At the second stage of deformation, parallel to the increase in current radius of hole edge, formation of flange vertical wall begins, and at the final moment of deformation all material elements receive the set deformation value in circular direction defined by the relation of values of the hole and the deforming tool. On fig. 5 ways and distributions of deformations are presented at different deformation values of the hole edge for deformation hardening parameter n = 0.2 .
Taking into consideration that deformations cannot accept zero values on border of non- deformable blank part of preparation (φ = 11π / 6 ) step-wise, dashed lines on figure 5 mark the zone of smooth reduction of deformation intensity from current sizes to zero. At the second stage of deformation the forming process has strongly pronounced non-stationary character at which there is a continuous change of sizes of plastic deformation sites. The impossibility of definition of current values of deformation components from equation (7) analytically is connected with the impossibility of its representation in the form of explicit function from parameter φ and deformation value of the hole edge. Therefore definition of current values and character of change deformation components is carried
Distribution of deformation at second Stage of deformation (curves of 1 and 2-7-Deformation distribution on initial and subsequent stages of deformation, directions 4π/3 ……11π/3. Line no.8 is the greatest circular deformation) out by graphic projection of vector function ε i (φ, εkp ) on oblique-angled coordinate axes ερ , εθ , εz Graphs of change of current values of deformation components are presented on figure 5 at the variable deformation site for n=0.2.
Presented figures show that for the whole deformation site deformations by thickness are negative, whereas deformations in circular direction are positive. Radial deformations in direction φ = 3π / 2 change sign and, as a result, during the forming process one part of deformation site undergoes radial compression, and the other undergoes biaxial stretching.