Anti-Atom Falling Up or Falling Down?

Abstract

Using an imaginary experiment of atom and anti-atom system annihilation around the earth, I find that the anti-atom should be 5 times as heavy as atom if I assume General Relativity correctly describes the gravity between matter, light and the earth.

Keywords

Anti-atom, Gravity, General relativity, Atom-anti-atom annihilation

Introduction

Recently in CERN there is a project of producing anti-atom and measuring the gravitational force between anti-atom and earth. Many would expect that anti-atoms will “fall up” instead of “fall down”. In this paper, it is shown that by our present knowledge of General Relativity on Matter and by the phenomenology of particle physics, it is already sure to deduce that gravitation between anti-atom and earth is 5 times stronger as that between atom and earth.

Description of the Imaginary Experiment

Figure 1 below is a description of the imaginary experiment: Suppose atom and anti-atom of the same mass come close very slowly to each other, and finally annihilate into two gammas. The two gammas can be in any direction, but we assume they both are in horizontal direction just to make the calculation easy.

Figure 1: Atom and Anti-Atom come close above earth (see (a)) and Annihilate into two Horizontal Gammas (see (b)).

The main motivation is to track the whole system of two atoms and two gammas since if we assume the atom falls down at g, and the two gamma bending toward earth with known formula, so we can extract the only unknown quantity: the acceleration of anti-atom [1-4].

Calculation of the Two Gamma System Movements with General Relativity

Since the two gammas are left right symmetric, so calculating one is enough to know all the two gamma system. Figure 2 below shows the quantities in the calculation for the gamma to the left.

Figure 2: Quantities referred to in the calculation of the bending of light by earth.

It is not necessary to solve Einstein’s equation from the beginning since in any of General Relativity book there is a ready formula there. We directly take one equation from Steven Weinberg’s book as follows:

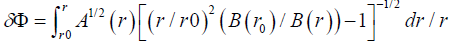(1)

And as usual

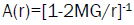(2)

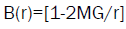(3)

This integral can only be done numerically, but if we only care about small δФ and hence small change of r, we can get (assuming r=r0 (1+x))

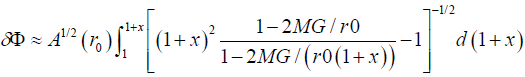
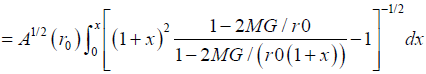
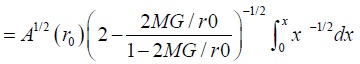
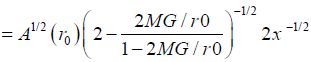
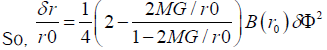
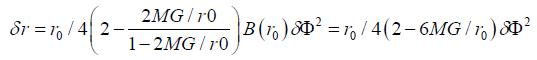
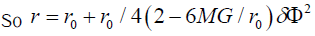(4)

Since the two Gammas are left-right symmetric, so the average position of horizontal Axis is zero

And the vertical position

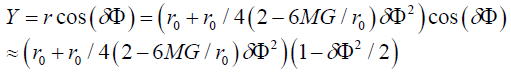
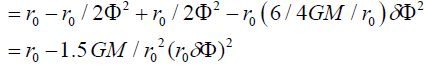
So the acceleration of the whole gamma system a=3 GM/ r02=3g

Determining the Gravitation between Anti-Atom and Earth

Let me reiterate the process as follows:

The whole system initially consists of Particle Anti-Particle of Mass 2 m; We know that the acceleration of particle is of g, and the acceleration of anti-particle is to be determined; the whole system annihilate into two gammas, and the whole system fall down with acceleration of 3 g (at least at a short time as the two gammas are not separated to the scale that comparable to earth); Since the annihilation is a kind of internal interaction of the closed system, so the earth does not know this, and should apply the same acceleration to it before and after the annihilation, so the system of particle anti-particle should also fall down with 3 g which means the anti-particle falls down with 5 g.

It is easy to show that such force should also be inverse square law with distance.

Conclusion

Anti-Atoms will be 5 times heavier than atoms, and the attractive force is also inverse square law with distance.

References

1. Simmons JFL, et al. The restricted 3-body problem with radiation pressure. CelestMech. 1985;35:145-187.
2. Kunitsyn AL and Turesbaev AT. Stability of the coplanar libration points in the photogravitational restricted three-body problem. Soviet Astron. 1985;11:391-392.
3. Singh J and Ishwar B. Stability of triangular points in the generalized photogravitational restricted three-body problem. Bull AstrSoc India. 1999;27:415-424.
4. Singh J. Combined effects of oblateness and radiation on the nonlinear- stability of L4 in the restricted three-body problem. Astron J 2009;137:3286-3292.