Beyond the Metrics: Qualitative Introduction to the Modified Gravitation

Abstract

As clearly suggested by the title, the aim of this paper lies essentially in providing a simplified introduction to a theory of modified gravitation. And it is easy to understand how the theory in question, very simply, is entirely based upon the conservation of energy. Our Universe, imagined as characterized by at least another spatial dimension, is hypothesized as belonging to the so called oscillatory class, although the variation of distances is not to be intended as a real phenomenon. More precisely, the radius of curvature of the Universe apparently evolves following a simple harmonic motion. Coherently with our perception of reality, matter can be initially imagined as evenly spread on the surface of a four dimensional ball. Actually, once admitted the existence of a further spatial dimension, it would be better to state how, at the beginning, matter homogeneously fills the ball in its entirety. Subsequently, matter can be shared out in different ways, keeping the total amount constant, so as to produce gravitational singularities, herein considered as merely punctual, non rotating and non charged. Time is supposed as being absolute: in other terms, the gravitational source does not produce any real time dilation. The measured distance between the gravitational source and a generic point is not influenced by the value of the mass that generates the field. Therefore, if we consider two generic points, and one of them, taken as origin, acquires mass, the measured distance between the aforesaid points does not undergo any modification whatsoever. Under the above mentioned hypotheses, by ascribing a different meaning to the coordinate usually identified with the distance between the source and any point in the field, a fully Newtonian form for the gravitational potential may be recovered.

Keywords

Oscillating universe; Non metric solution; Newtonian gravitation; Modified gravitation; Schwarzschild radius

Introduction

Let's suppose that our Universe is characterized by (at least) another spatial dimension. Coherently with our perception of reality, with the usual hypothesis of homogeneity and isotropy, matter could be imagined as evenly spread on the surface of a four dimensional ball. Actually, having assumed the existence of a further spatial dimension, taking into account the symmetry, each material point has to be replaced by a material line segment bordered, on one side, by the center of the ball. In other terms, the Universe is no longer assimilated to a three dimensional spherical shell (a hyper sphere), but rather to a closed 4-ball. Moreover, the Universe is imagined as belonging to an oscillatory class characterized by a null curvature parameter and a negative cosmological constant [1].

As previously said, at the beginning, in absence of gravitational effects, the whole mass may be considered as evenly spread on the surface of the four dimensional ball (actually, according to what supposed, matter homogeneously fills the ball).

Referring to Figure 1, the circumference centered at O' is simultaneously border of a disk, whose center obviously coincides with O' itself, and of a spherical cap, whose amplitude is double the angular distance between O, taken as origin, and a generic point P belonging to the above mentioned circumference.

Generally, denoting with x the flat coordinate (the forecast one), we have:

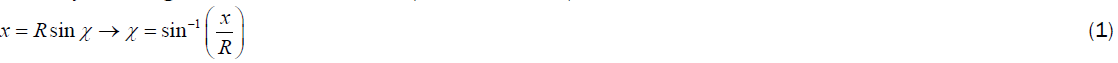
Denoting with l the measured distance, we have:

By introducing the dimensionless coordinate r

and the scale factor a

From (3) we can write:

Under the light of the previous considerations, we may easily understand the following identity:

The relation we have just considered represents, with obvious meaning of symbols and signs, the so called Robertson- Walker metric, written by setting the curvature parameter equal to one. As well known, this metric is suitable for a closed Universe, isotropic and homogeneous, characterized by a positive curvature whose value depends on time. It is worth underlining how, for the oscillating universe we have hypothesized, we have to consider a global curvature parameter equal to zero. In fact, although the reality we are able to perceive may be effectively represented by a three dimensional curved space, Universe in its entirety has to be imagined as characterized by at least four spatial dimensions.

Referring to Figure 2, let's consider a spherical cap, characterized by amplitude equal to 2χ_max. Q represents a generic point of the border (a circumference whose radius is equal to the straight line segment bordered by O' and Q itself).

We can write the forecast radius as follows:

For the measured radius we can write:

What we imagine to be a disk is actually a spherical cap. In particular:

What we imagine to be a ball is actually a hyperspherical cap. In particular:

By using Taylor approximation, we can write:

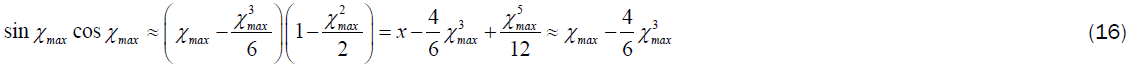
As a consequence, by (15) and (16), the hyperspherical cap is well approximated by a sphere whose radius is equal to Rχ_max

Now, let’s imagine we can concentrate in a single point the mass included in the hyperspherical cap characterized by an amplitude equal to 2χ_max. According to what initially supposed, the procedure is equivalent to concentrating the mass contained in the hyperspherical sector, characterized by the same amplitude, along the material line segment bordered by the center of the ball and by the point O. Due to the procedure we have carried out, the point will change its radial coordinate: in other terms, the material segment will undergo a contraction and the shape of the space from which we have taken away mass will result modified. The straight line segment bordered by C and O’ represents the new radial extension of the singularity. The straight line segment bordered by C and P’ represents the radial coordinate of a generic point, initially placed in P, after having carried out the above mentioned procedure.

Generally, if a curve f(χ) is expressed in polar coordinates, its length is provided by the following relation:

Now, we have to impose a fundamental condition: the measured distance between any point and a generic gravitational source, imagined as punctual, does not undergo any modification whatsoever. If the radial coordinate, denoted with z, is exclusive function of the angular distance (as perceived by an ideal observer placed at the center of the ball), in order to satisfy the previous condition it has to be:

As a consequence, we have

Therefore, we have to solve the banal second order linear homogeneous differential equation

With the following boundary conditions:

The general solution is

By virtue of the foregoing, taking into account conditions (23) and (24), C1 and C2 can be easily deduced as follows:

Finally we obtain:

Figure 2 lets us clearly understand we could have reached the previous result by following a merely geometric line of reasoning.

If we denote with h the difference between the radius of curvature and the value of z, from (32) we can write:

Discussion

The conservation of energy (and the equivalence principle [2]) can be expressed as follows [3]:

m represents the mass at rest of a test particle (the mass is not sufficient to produce spatial deformations), and m_z the corresponding modified mass, banally defined by introducing the linear density:

If the motion is produced by a gravitational field we may write:

Moreover, referring to a general metric, since it has to be

By taking into account (39) we can immediately write:

Given that the previous relations could be misleading, it is fundamental to underline how time does not undergo any real modification. It is worth specifying that the apparent time dilation expressed by the first component of the metric tensor is exclusively related to the contraction of the orbits.

Obviously, the potential can be expressed as follows:

Let’s initially discuss the following particular case. Very simply, we have to suppose that the whole mass of the Universe may be concentrated in a single point (obviously, the center of the ball). The scenario is represented in Figure 3.

Under the above mentioned condition, taking into account relation (32), it must necessarily be:

Now, we have to suppose that our Universe may oscillate following a simple harmonic motion. If we denote with R_m the amplitude of the motion (the mean radius), with c the speed of light, and with ω the pulsation, we can write:

Let’s denote with M_m the mass of the Universe (actually half the value of the mass-energy) when the radius of curvature is equal to R_m. Under specific conditions [4], the amplitude of the harmonic motion coincides with the Schwarzschild radius [5]:

Obviously, G represents the gravitational constant. From the previous position we immediately obtain:

As a consequence, underlining how the variation of distances is not to be considered as a real phenomenon, assuming the mean values as actual, by virtue of (39) and (48), we can state the following:

By carrying out the underlying position

from (49) we immediately obtain:

Obviously, it evidently turns out that

Moreover, remarking again how Rm is nothing but the Schwarzschild radius of the Universe, we have:

Bearing in mind that, due to the symmetry, all the energetic quantities in (36) are doubled, with the usual convention concerning the potential difference, we obtain the following pseudo Newtonian form:

By using relation, (32) it's easy to verify how, when the measured distance is equal to zero (or, equivalently, when the angular distance is null), the coordinate R*equates the Schwarzschild radius. In fact:

If we had wanted to deduce a fully Newtonian expression, we should have written (38) by considering a relativistic potential:

By virtue of the foregoing, we obtain:

By carrying out the following new position

We can immediately write once again relations (51) and (56).

However, this time we have:

Let's consider now the general case: the singularity is provided with a mass whose value is inferior to the one of the Universe. More precisely, we can imagine concentrating in a single point a mass equal to the one contained in a hyperspherical sector characterized by an amplitude equal to 2χ_max.

The potential can be written as follows

As a consequence, taking into account equations (33) and (35), the maximum value of the potential proves to be:

From the two previous equations we immediately obtain:

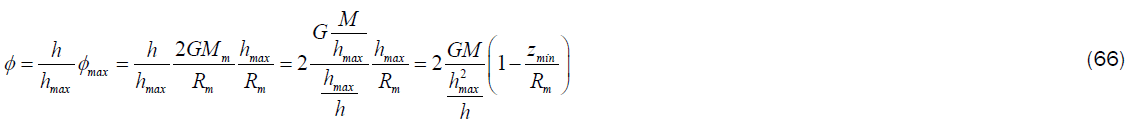
The potential may be normalized as follows

so as to obtain:

Now, we can carry out the following position:

Obviously, from (35), denoting with Rs the Schwarzschild radiuses, we have:

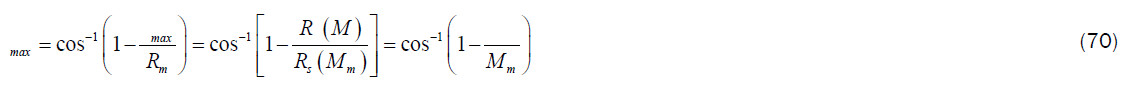
Finally, with the usual convention already used in (56), we obtain:

Alternatively, we could have modified the gravitational constant as follows

So obtaining:

It may be interesting to notice how, due to the symmetry, we could represent the gravitational source as a non-genuine singularity. In two dimensions, the material point that produces the gravitational field turns into a circumference (actually, a spherical surface), whose radius is exactly equal to the Schwarzschild one. The scenario, qualitatively depicted in Figure 4, may be obtained by rotating the modified profile, previously represented in Figure 2, around the straight line, orthogonal to the sheet plane that crosses the point O, taken as origin.

If we had carried out the above mentioned procedure by rotating the profile around the straight line, orthogonal to the sheet plane, that crosses O' (the genuine singularity), we would have obtained a gravitational spherical domain characterized by a radius provided by (8).

Conclusion

Coherently with the title, this paper yearns to provide nothing but a premise, whose full comprehension should be easily achieved by taking advantage of what specified in the introduction, to a theory of modified gravitation. The Universe, hypothesized as provided with at least another spatial dimension, is supposed as characterized by a constant mass, initially evenly spread, as far as our perception of reality is concerned, on the surface of a 4-ball. The mass can be shared out in different ways, keeping the total amount constant: in this paper, obviously, we have exclusively examined punctual singularities, non-rotating and non-charged. The fundamental hypothesis consists in imposing that the measured distance between the gravitational sources, imagined as punctual, and any point in the field does not depend on the mass. Time is supposed as being absolute: as a consequence, a gravitational source is not able to produce time dilations. The first component of the metric tensor, barely mentioned in order not to sound too much off topic, has to be related to the contraction of the orbits, that takes place in spite of the fact that the measured radiuses do not undergo any variation whatsoever. Among the focal points, it is worth underlining that, according to the proposed simplified model, the Newtonian form can be preserved. We have to simply admit that the coordinate that characterizes the Newtonian potential, usually identified with the distance between the gravitational source and a generic point in the field, may have a quite different meaning. Although several metric solutions, based upon the considerations expressed in the article, could have been easily deduced, we have preferred to follow a line of reasoning that should allow, in a certain sense and measure, to concretely visualize a scenario that could turn out to be more understandable than one may imagine.

References

1. Harrison ER. Classification of uniform cosmological models. Monthly Notices of the Royal Astronomical Society. 1967;137: 69-79.
2. Einstein A. Relativity: The Special and General Theory (translated by Lawson RW, 1920). Henry Holt and Company, New York. 1916.
3. Cataldo C. Towards a new Relativity: how to travel faster than light. Research & Reviews: Journal of Pure and Applied Physics. 2016;4.
4. Cataldo C. A simplified model of Oscillating Universe: alternative deduction of Friedmann-Lemaître equations with a negative cosmological constant. Research & Reviews: Journal of Pure and Applied Physics. 2016;4.
5. Schwarzschild K. Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik. 1919;189-196.