Research & Reviews: Journal of Pure and Applied Physics
MenuISSN: 2320-2459
ISSN: 2320-2459
Carlos Alberto Stechhahn de Silva*
Department of Physics, Criminalistic Institute of São Paulo, Brazil
Received: 10-Jan-2023 Manuscript No. JPAP-23-86408; Editor assigned: 13-Jan-2023 Pre QC No. JPAP-23-86408(PQ); Reviewed: 27-January-2023, QC No. JPAP-23-86408; Accepted: 03-February-2023, Manuscript No. JPAP-23-86408(A) Published: 10-February-2023,DOI:10.4172/2320-2459.11.1.001
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
In this work, we consider a particle moving on a two-dimensional non-commutative plane immersed in a constant magnetic field. The non-commutativity of spatial coordinates, conjugate momentum, and spin variables are supposed to satisfy a "non-standard" Heisenberg algebra. The parameterθ that characterizes the non-commutativity here is not constant and is called "non-commutativity of spin". Using the Pauli equation and perturbation theory, the non-commutativity parameter can be shown, after considering the degeneracy of energy levels, to be bounded by θ<< 10−20 cm.
Pauli equation; Spin non-commutativity; Non-commutative quantum mechanics
Theories in non-commutative space have recently attracted a great deal of interest [1]. This interest has its origin in quantum gravitation, string theory, black holes, cosmology, and even the very conceptual basis of field theory [2-13]. Non-Commutative (NC) spaces are characterized by position operators xˆμ satisfying the relationship.
[ xˆμ , xˆv ]=i θμv,… (1)
Where θμv is a constant antisymmetric matrix of dimension (length)2 and the hatted quantities refer to position operators in NC space. The field theory formulated on these spaces (i.e., non-commutative field theory) is described by field operators, which are functions of xˆμ In NC field theories the punctual field product is exchanged by the Moyal field’s product,
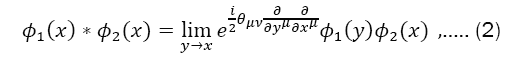
WhereΦ1(x)and Φ2(x)are two arbitrary and infinitely differentiable functions, thus giving rise to nonlocal theories. From the nonlocality inherent to Eq. (1) several peculiarities appear from non-commutative theories. One of these properties is the so-called ultraviolet-infrared (UV-IR) mixture, which consists of infrared singularities arising from ultraviolet divergences, even in theories with no fields of zero mass [14]. Except for some supersymmetric theories [15,16], UV-IR mixture destroys the usual disturbing schemes. Another peculiar aspect resulting from nonlocality is unitarity and causality when θoi≠0[17].
In all these situations, we have canonical non-commutativity [18]. A great deal of literature has been devoted to exploring the consequences of this type of non-commutativity in several theoretical fields and quantum-mechanical models [19-21].
We examine here a new type of non-commutativity, namely, one that depends on spin [22,23]. This type of consideration for non-commutativity encourages the construction of new models in quantum mechanics [24-26]. New research paths in this sense can be explored (for example, nonconventional superconductivity [27] and a geometric picture of quantum mechanics [28]. Discusses various questions about the physical meaning and mathematical formulation of spin-dependent non-commutativity [29].
More recently, the effects of the non-commutativity of the space-time with mixed spatial and spin degrees of freedom in a relativistic situation [30] allows us to explore new routes to Quantum Gravity Theory. In this regard, it leads to the understanding that the space-time has an underlying structure on small distance scale - or high energy scale - leading to some of the long-standing research in recent years.
The non-commutativity of the spatial coordinates θ, the conjugate moment pˆi, and the spin variables,sˆi are supposed to satisfy the "nonstandard" Heisenberg algebra.
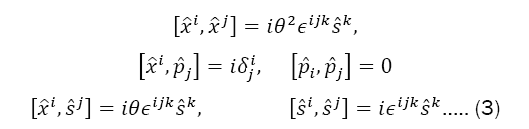
Where θ is the non-commutative parameter that we call non-commutativity spin dependent? The procedure we adopt consists of relating the position operators xˆi.which satisfies Eq. (3), to the commutative operator xithis transformation, usually called the Bopp shift, is respectively given for coordinates and momenta by
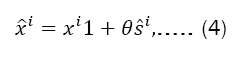
Where, in terms of Pauli matrices,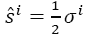 
is the spin operator.
To understand the implications of this new type of non-commutativity, we use the Pauli equation in what follows to study its perturbative effect in a nonrelativistic situation.
The Pauli equation
We consider the movement of a particle of charge e in x-y plane subject to a magnetic field B→ perpendicular to the plane (i.e., in the z direction). The Pauli-Hamiltonian is given by
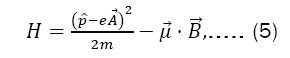
So that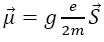 
the magnetic moment, g is the gyromagnetic vector, S→ is the spin, and the components of the electromagnetic potential are
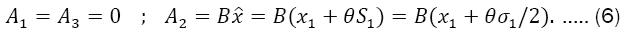
Replacing the above components in Eq. (5) leads to the following eigenvalue equation
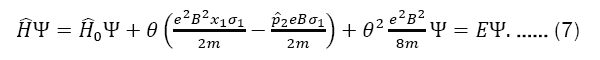
The term proportional to θ2 give us a constant displacement across all the spectrum and henceforth is omitted. For the calculation of the undisturbed solution (θ=0), the operator
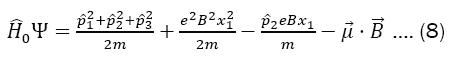
Has no explicit y and z coordinates. Therefore, the operators pˆ2,pˆ3, commute with Hˆ0, that is, the components y and z of the momentum are conserved. We thus adopt the following solution:
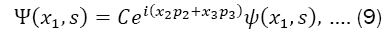
where C is a normalization constant. Upon substituting this solution into our expression (7), we get
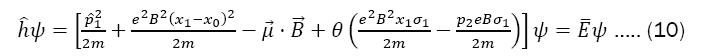
where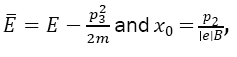 
which can be solved perturbative by means of the equation
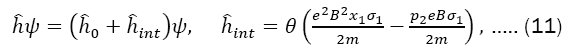
where 
is the Hamiltonian of the Landau problem:
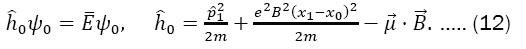
The solutions 
are separable as follows
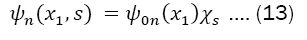
So that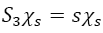 
and
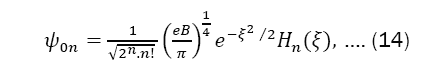
where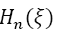 
represents the polynomials of Hermite,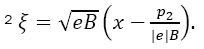 
The eigenvalues are given by
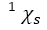Describes the spin projection along the magnetic field.
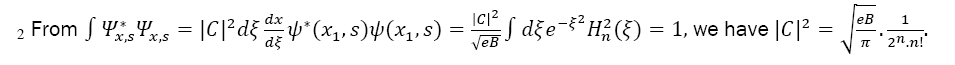
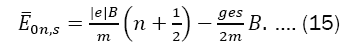
In particular, to an electron, neglecting radioactive corrections,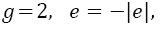 
and the result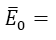
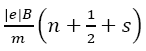shows that the energy level for a given
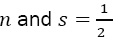is in fact degenerate with the level n+1and s=-1/2 We thus analyze the conditions given in the following sections.
Nondegenerate energy levels (g≠2)
In this situation we use nondegenerate perturbation theory to compute the dominant correction to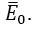
However, the first-order correction is
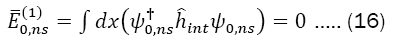
Since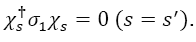 
Therefore, we must examine the second-order perturbation formula
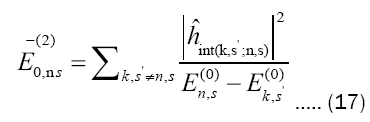
So, for s'≠s, we get after some calculations
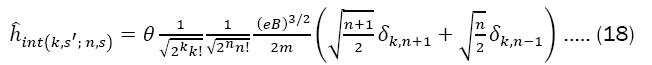
Where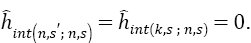 
In this way, the array elements nullify to k=n and s'≠s as well as to k≠n s'= s Hence, the second-order correction for energy is
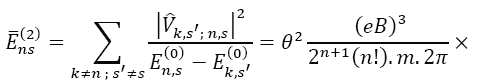
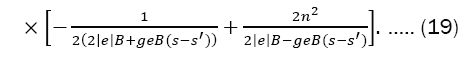
Degenerate energy levels fixed by the Hamiltonian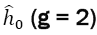 
In this situation, we have to solve the secular equation to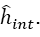 
. The solution is simple since 
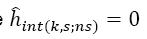and
It follows that the degeneracy is broken by the first-order correction. The original level splits into
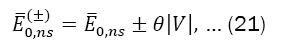
Where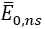 
is given by Eq. (17) and
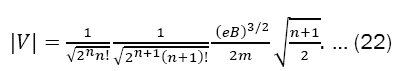
Equations (21) and (22) allow us to estimate the value of the non-commutative parameter θ. Since,
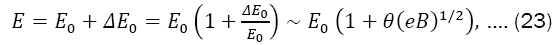
And considering the strength of the magnetic field typical of the nucleus of a neutron star [31], of the order of 1013, we have:
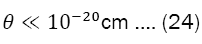
In which we assume the accuracy of the results of the quantum Hall effect of the order of atomic measurements. In addition, the two linearly independent zero-order wave functions suitable for perturbative calculations are
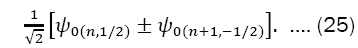
In the present work, we study non-commutative quantum mechanics and consider in particular spin-non-commutative effects. Using the Pauli equation, corrections for the energy were calculated up to second order for a particle in a constant magnetic field. The unperturbed Hamiltonian shows a continuous degeneracy and, in the case of the electron (g=2), a discrete degeneracy. The continuous degeneracy persists and the discrete degeneracy is modified by the disturbance.
3 1G=104 T, and, in natural units, B=1 eV2 = 1,44.10−3 T.
All these studies do not rule out the possibility of their application to relativistic situations. In the relativistic problem, with θ=0, the same degeneracy occurs as in the nonrelativistic problem and can be either continuous or discrete. We consider the strength of the magnetic field B of the order of 1013G. The non-commutativity parameter can be shown to be bounded as θ<< 10−20cm.
In recent years, several studies have been devoted to Non-Commutative (NC) theories and these represent an intense effort to understand the properties of space-time at very small length scales.
The idea of taking space-time coordinates to be noncommutative have attracted great interest through the multiplicity of its applications. In these (NC) spaces, much of the literature usually employs the most diverse tools and areas, such as: “path integrals”, “1/N expansion”, “quantum field theory” [1, 32-34], etc.
In the present work, in noncommutative quantum mechanics we apply “perturbation theory”, a systematic procedure for obtaining approximate solutions to a perturbed Hamiltonian, and consider in particular spin-noncommutative effects. Here, the NC theta parameter is used as the parameter of the perturbation on which the expansion is done.
Using the Pauli equation, we see that the Hamiltonian has its θ dependence on the second component of the vector potential. From the eigenvalue equation we obtain the free and interaction Hamiltonians. The solutions of eigenvalue equation to the unperturbed Hamiltonian are expressed in terms of Hermite polynomials and the normalization constant have been calculated.
We start with the condition that (g=2), i.e., to the nondegenerate perturbation. In this case corrections for the energy were calculated up to second order for a particle in a constant magnetic field.
Finally, we consider the situation where the energy levels are degenerate (g=2). We solve the secular equation to the perturbed Hamiltonian and we observe that the degeneracy is broken by the first-order correction. The original level splits into two values for the energy.
Our next step was to consider the strength of the magnetic field typical of the nucleus of a neutron star. The noncommutativity parameter can be shown to be bounded as θ<< 10−20cm. It is important to note we work in natural units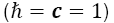 
which in this case 
We can find in literature other approaches based in noncommutative quantum mechanics such that proposed by Gamboa et al. In the context of Landau problem [35]. There, to the magnetic field about 12 T the result obtained was θ=0.22×10−11cm2. Later, in Bose-Einstein condensation theory context, a similar result was presented [36].
Nowadays there are several bounds for θ[37-39]. New limit for the noncommutative spacetime parameter can also be found.
Appendix: The Moyal product of two fields
We now use the expression for Φ(x)in terms of the trace to build the Moyal product of the classical funΦ1and Φ2 corresponding to the product of operators Φ1and Φ2:
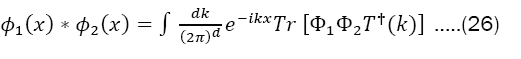
Since
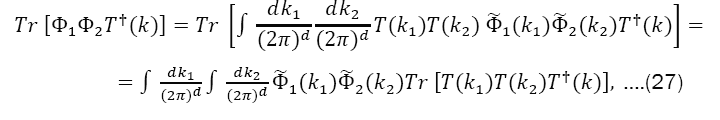
Where
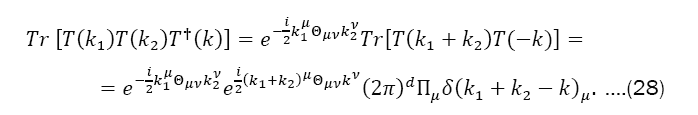
Replacing Eq. (28) into Eq. (27), Eq. (26) becomes
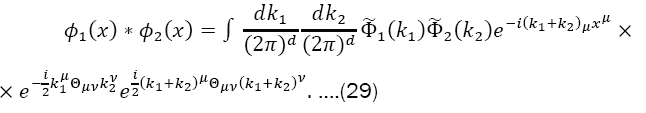
However,
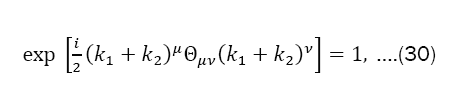
So,
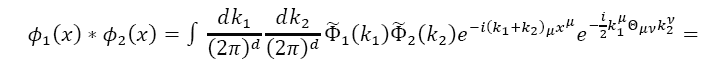
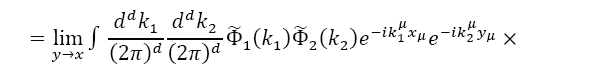
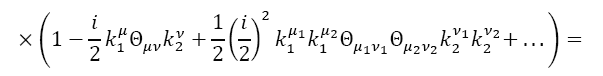
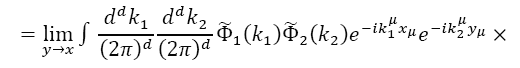
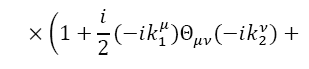
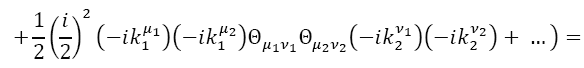
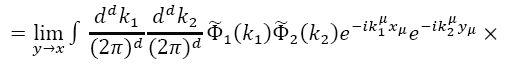
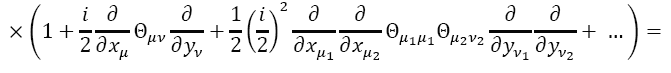
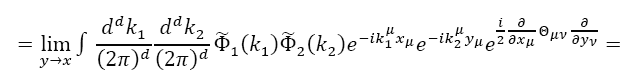
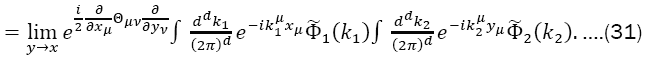
Thus, we have the following expressions for the Moyal product of two fields:
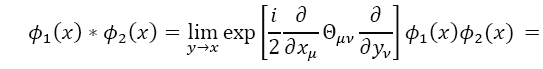
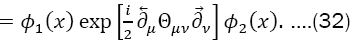
The study of a non-commutative space-time has grown very fast in recent years. Several attempts have been made to search for possible effects of non-commutativity in different frameworks. In particular, experiments investigating the spin effects of cold atoms in gases. Non-commutative quantum mechanics is currently contributing, with an important portion of work on non-commutativity, in different forms of study. It permits us to examine phenomena that occur at very small scales and to explore the physical consequences in a simpler situation. Finally, in face of the tiny non-commutativity contributions, we hope that the Tonomura-type experiments can probe the spin non-commutativity in the near future. All these studies do not rule out the possibility of their application to relativistic situations. In the relativistic problem, with θ=0, the same degeneracy occurs as in the nonrelativistic problem and can be either continuous or discrete.
[Crossref] [Google Scholar] [PubMed]