ISSN: 2320-2459
ISSN: 2320-2459
1Department of Mathematics, College of Arts and Science, Prince Sattam bin Abdulaziz University, Saudi Arabia
2Department of Mathematics, Anand International College of Engineering, Jaipur-303012, India
3Department of Applied Mathematics, Aligarh Muslim University, Aligarh, India
4Department of Mathematics, Poornima College of Engineering, Jaipur, India
Received: 14/10/2015 Accepted: 12/11/2015 Published: 15/11/2015
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Suitable manipulations in Rodrigues type formulae can lead to numerous other type of formulae which are significatly important and are expected to find applications in probability theory and boundary value problems. Using Leibnitz formulae for nth derivative of the product of two and three functions some elegant Rodrigues type formulae for polynomials corresponding to ф1 function and Appell’s F1 function have been derived.
Rodrigues formula, Polynomials, Arbitrary, Probability theory, Value problems, Manipulations, Special functions.
Using Leibnitz formulae for nth derivative of the product of two and three functions some elegant Rodrigues type formulae for polynomials corresponding to ф1 function and Appell’s F1 function have been derived. In recent years, many authors have been consider the ф1 function and Appell’s F1 type function in their studies [1-6]. In deriving the operational representations of various polynomials, we use the following fact that
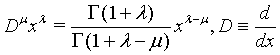 (1)
(1)
Where λ and μ , λ ≥ μ are arbitrary real numbers. In particular, use has been made of the following results [7-12]
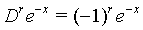 (2)
(2)
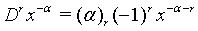 (3)
(3)
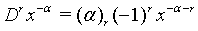 (4)
(4)
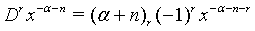 (5)
(5)
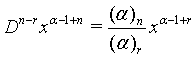 (6)
(6)
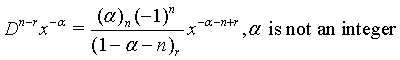 (7)
(7)
where n and r are denote positive integers and
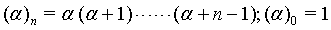 (8)
(8)
Further,
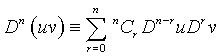 (9)
(9)
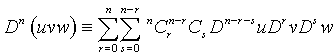 (10)
(10)
we also need the following definitions [4,5,13,14].
The Appell’s F1 function defined by
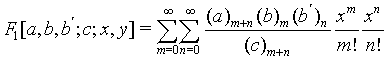 (11)
(11)
and the confluent hypergeometric function φ1 is defined by
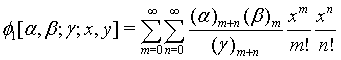 (12)
(12)
Rodrigues Type Formula
In this section we developed Rodrigues type formulae for F1 and ф1 functions
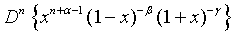
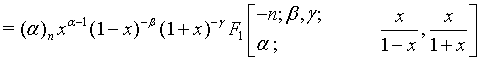 (13)
(13)
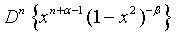
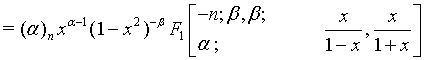 (14)
(14)
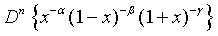
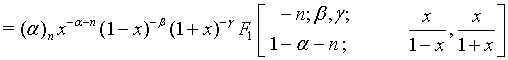 (15)
(15)
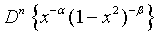
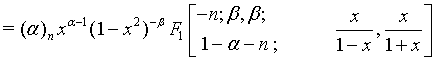 (16)
(16)
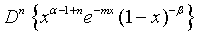
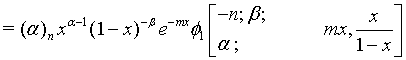 (17)
(17)
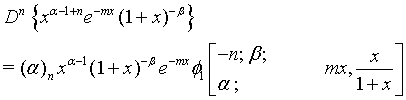 (18)
(18)
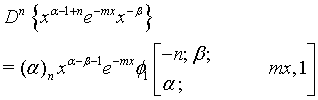 (19)
(19)
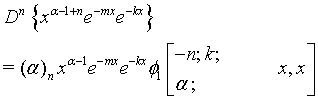 (20)
(20)
Proof of 13:
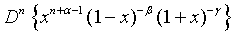
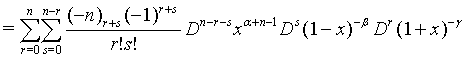
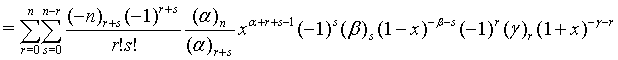
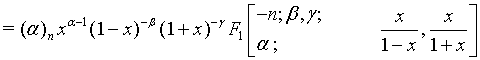
Proof of 16:
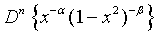
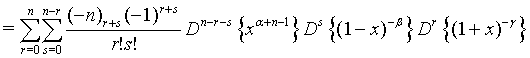
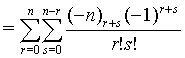
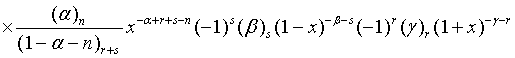
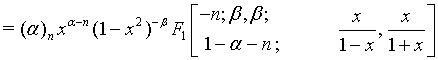
Proof of 17:
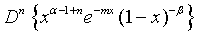
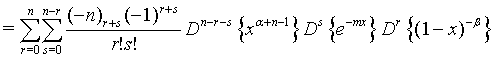
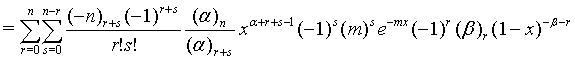
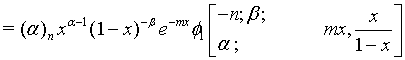
Proof of 18:
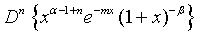
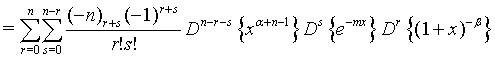
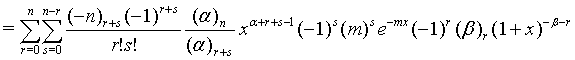
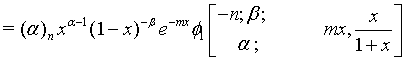
Proof of 19:
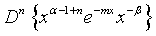
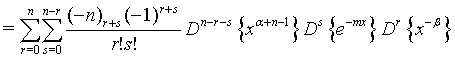
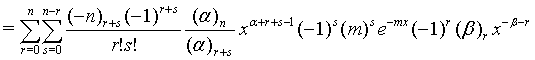
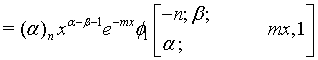
Proof of 20:
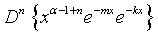
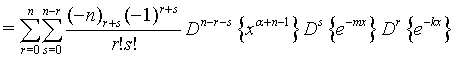
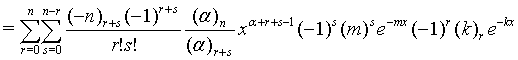
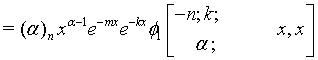
Similar way one can prove all the equations.
We conclude this paper by noting that, the results deduced above are significant and can lead to yield numerous other Rodrigues type formulae involving various special functions by suitable manipulations. More importantly, they are expected to find some applications in probability theory and boundary value problems.