ISSN: 2320-2459
ISSN: 2320-2459
Jagadamba Prasad Vishwakarma* and Rajendra Kumar Srivastava
Department of Mathematics and Statistics, D.D.U. Gorakhpur University, Gorakhpur-273009, India.
Received date: 20/09/2013 Revised date: 25/09/2013 Accepted date: 30/09/2013
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
This paper analyses the propagation of converging cylindrical detonation waves in an ideal gas with varying initial density and varying azimuthal magnetic field. The Chester-Chisnell-Whitham (CCW) method was employed to determine the detonation front velocity and the other flow-variables just be- hind the shock in the case when (i) the gas is weakly ionized before and behind the detonation front, (ii) the gas is strongly ionized before and behind the detonation front and (iii) non-ionized (or weakly ionized)gas undergoes intense ionization as a result of the passage of the detonation front. It is investigated that in case (i) an increase in the value of the strength of initial magnetic field (M−2cj) shows almost negligible effect on the convergence of the detonation front and the pressure behind it, while an increase in the value of ratio of specific heats of the gas (γ), increases the velocity of detonation front and the pressure behind it near the axis. A decrease in the value of index for variable density α, accelerates the convergence of front and increases pressure behind it. In the case (ii) on increasing (M−2cj), when α = 0, the front velocity near the axis and the pressure behind it decrease. A decrease in the value of α increases the velocity of the detonation front and the pressure behind it. An increase in the value of γ in non-magnetic case, rapidly increases the velocity of detonation front and the pressure behind it. In the case (iii), the variation of M−2cj and α, show similar behaviour as in case (ii), but an increase in the value of γ rapidly increases the pressure behind the detonation front.
Detonation wave, ideal gas, variable azimuthal magnetic field, CCW method, variable initial density.
The converging detonation wave has intrigued researchers for decades due to its inherent implosion ability. The converging geometry forces the detonation wave front into an ever-decreasing area that creates additional compression as compared with that of planar geometries. The end result is a positive feedback-cycle, i.e. the increasing compression accelerates the overdriven detonation, which, in turn, acts to further increase the post-detonation pressure and temperature (Jiang et al. [1]. This cycle continues during the converging process and can result in an overdriven detonation with extremely high post-detonation pressures and temperatures. The problem of converging shock was first solved by Guderley [2]. The similarity solution was presented and the self-amplifying character of the wave was suggested. This gives a shock of infinite strength at the centre of convergence. Payne [3]] has given a numerical solution for a converging cylindrical shock. Stanyukovich [4]] has discussed the problem of a contracting spherical or cylindrical shock front propagating into a uniform gas at rest. Terao et al. [5,6]] carried out experiments on a spherically converging detonation wave in a stoichiometric propane-oxygen mixture at an initial pres- sure of 40KPa and a room temperature of 293 K. Zel’dovich and Raizer [7] have summarized two kinds of self-similarity, and in the second kind, have described the implosion of spherical shock in a gas and the collapse of spherical bubbles in a liquid.
The self-similar solution, describing imploding shocks, have asymptotic character because they describe the process of implosion in a region near the axis (or centre) in which it is no more influenced by the initial conditions. The global solution, that is a solution that can describe the whole history of the fluid motion from the initial stage to focussing stage, was presented by Matsuo [8] by a non-similar approximated method.
The Chester-Chisnell-Whitham (CCW) [9,10,11] method is a very simple and effective method for analysis of imploding shocks. This method has found numerous applications, for example, the description of the propagation process of converging shock waves through a channel of variable section (Chisnell [10], in a dusty gas with variable density (Vishwakarma and Haider [12], in a conducting gas with variable density (Vishwakarma [13] and in a solid (Tyl and Wlodarczyk [14] and the analysis of imploding detonation waves (Lee and Lee [15]. Although the Whitham’s rule is approximate, but it agrees well with exact solutions and with experimental results (Lee [16,17], Jumper.
Nagayama [18] has given an experimentally verified (Nagayama and Mashimo [19] method for achieving very high pressure by compression of magnetic flux by means of a converging shock wave in a semiconducting material which becomes highly conductor due to passage of shock wave. Tyl and Wlodarczyk [20] studied cylindrical and spherical detonation waves converging in gaseous explosive mixture by CCW method. They applied the Chapman-Jouguet condition on the detonation wave in the initial position only, and obtained analytical solution describing its propagation in the absence of magnetic field. Their solutions agreed well with the experimental results. Vishwakarma and Vishwakarma [21] extended the case of converging detonation waves of Tyl and Wlodarczyk [19] to include the effects of the presence of an azimuthal magnetic field. They studied both the cases (i) when the gas is strongly ionized before and behind the detonation front (ii) when the non-ionized gas undergoes intense ionization as a result of passage of the detonation front. The combustible gas was assumed to obey the equation of state of a perfect gas (Vishwakarma and Chaubey [22].
In the present work, we analyse the convergence of a strong cylindrical detonation wave in an ideal gas (combustible) in the presence of an azimuthal magnetic field. The initial density is variable. It is assumed that the detonation wave is initially Chapman-Jouguet, i.e. initially it travels with velocity of propagation of small disturbances relative to the burnt gas (Helliwell [23]. The effects of the ratio of specific heats of the gas, the variable initial density of the gas and the azimuthal magnetic field are investigated. To our knowledge, the problem of converging detonation wave in a non-homogeneous ideal gas, which takes into account the effects of a variable azimuthal magnetic field, has not been studied previously.
During the experiments involving the implosion of a detonation wave in a gas, the following state may occur:
i) The gas is weakly ionized before and behind the detonation front,i.e. Rm<<1, where Rm is the magnetic Reynold number.
(ii) The gas is strongly ionized before and behind the detonation front, i.e. Rm>>1 or σ→∞, where σ is the electrical conductivity.
(iii) Non-ionized (or weakly ionized) gas undergoes intense ionization as a result of the passage of detonation front, i.e. σ increases in a jump like manner from 0 to ∞.
In our study, we analyse all the three cases when the initial magnetic field is azimuthal and variable. Chester-Chisnell-Whitham (CCW) method is employed to determine the velocity of detonation front and the other flow variables just behind the front.
Fundamental Equations and Boundary Conditions
The basic equations governing the unsteady and cylindrically symmetric motion of a weakly conducting ideal gas (Case I, Rm<<1) are given by (Tyl [24]

where ÃÂñ, u and p are the density, velocity and pressure at time ‘t’ and at distance ‘r’ from the axis of symmetry, γ is the ratio of specific heats, σ is the electrical conductivity, μ is the magnetic permeability, B is the azimuthal magnetic induction, B0 is the initial magnetic induction and ’a’ the speed of sound given by

The density and the magnetic induction of the gas ahead of the converging detonation front are assumed to be varying and obeying the laws:

where r0 is the radius of detonation front and K, A, α and α1 are constants.
Equations (2.1) to (2.4) can be combined to form the characteristic equation (Whitham [11], Tyl [24],
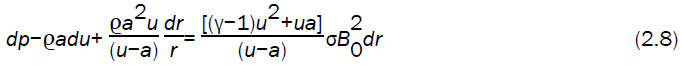
along the negative characteristic

The fundamental equations governing the unsteady flow behind a cylindrical magnetogasdynamic (Case II, Rm>>1) or gas-ionizing (Case III, σ : 0 →∞) detonation front are given by (Whitham [11],
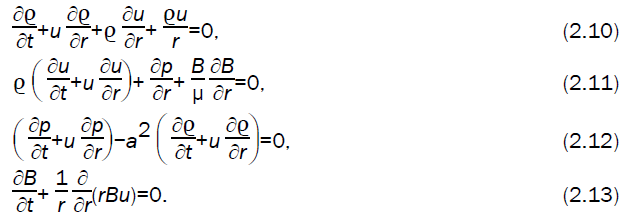
Equations (2.10) to (2.13) can be combined to form characteristic equation (Whitham [11]
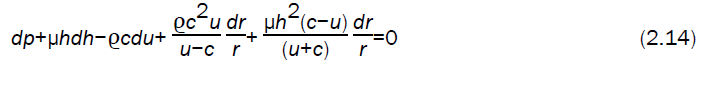
along the negative characteristic

where 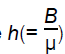 is the azimuthal magnetic field and c is the effective speed of sound given by
is the azimuthal magnetic field and c is the effective speed of sound given by
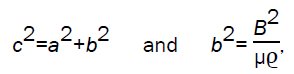 b being the Alfven speed.
b being the Alfven speed.
Since σ is small in the Case I, and σ is zero ahead of the detonation front in the case III, the magnetic induction may be taken continuous in these cases (Sakurai [25], Ranga Rao and Ramana [26]. The conditions across the detonation front in the cases I and III are therefore (Tyl and Wlodarczyk [14], Vishwakarma and Vishwakarma [21].
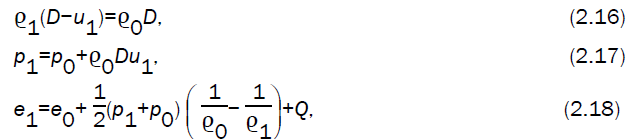
where D, Q and e denote the velocity of detonation front, the heat energy released per unit mass and the internal energy per unit mass, respectively. The indices ‘1’ and ‘0’ refer to the states just behind and just ahead of the detonation front.
In the pure magnetogasdynamic case (the case II), the gas is strongly ionized, i.e. highly conducting, before and behind the detonation front, upon which the magnetic induction may be discontinuous at the front resulting from a sheet current there (Sakurai [25]. The conditions across the detonation front, in this case, may be written as (c.f. Whitham [11])
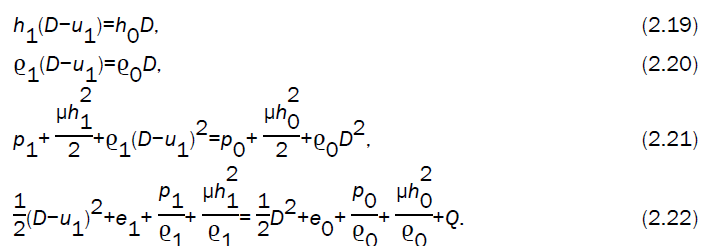
The detonation front is assumed to be strong, i.e. p0<<p1, therefore we take p0=e0=0 in the relations (2.16) - (2.18) and (2.19) - (2.22).
Solution of the Problem
The detonation front is assumed to be initially of radius R and in the Chapman-Jouguet state. The Chapman-Jouguet condition requires that the down stream flow will be sonic in the shock fixed co-ordinates, i.e.

where ‘cj’ refers to the Chapman-Jouguet state. Therefore, the conditions across the strong Chapman-Jouguet front, in the case I and III, are expressed as
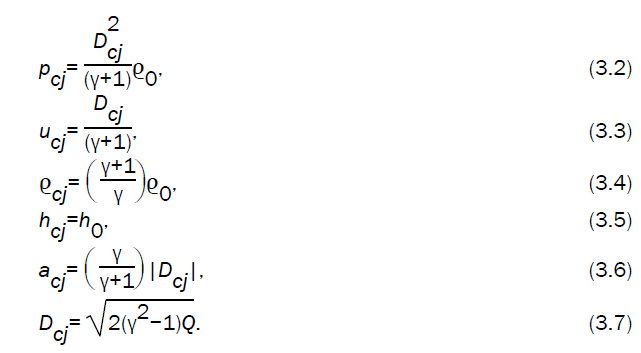
In case II, the magnetic field is also discontinuous across the front and therefore, the condition (3.5) is replaced by

Making use of relations (2.16) - (2.18) and (3.2) - (3.7), the conditions across the strong detonation front can be expressed in the terms of velocity of detonation products (burnt gas), in the case I, by the equations
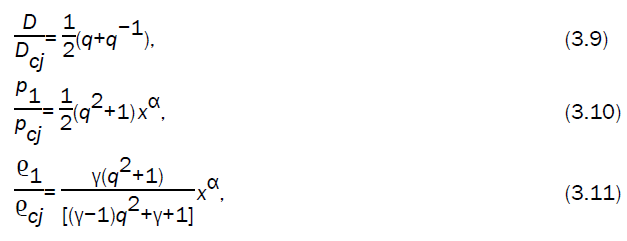

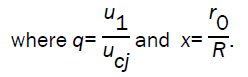
Using relations (2.19) - (2.22) and (3.2) - (3.8), the conditions across the strong magnetogasdynamic detonation front (case II) can be expressed by the equations
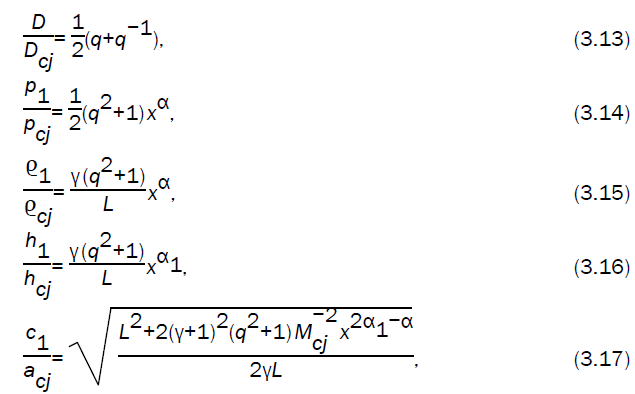
where 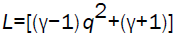 and the Alfven Mach number Mcj of the detonation front in the Chapman-Jouguet state is given by
and the Alfven Mach number Mcj of the detonation front in the Chapman-Jouguet state is given by
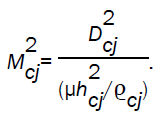
In the case III (strong gas-ionizing detonation front), the equations (3.16) and (3.17) are replaced by
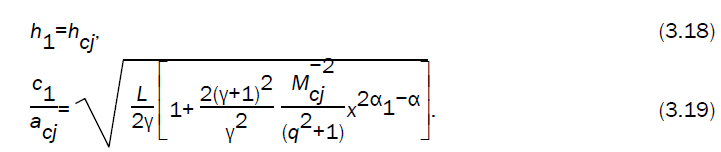
Now, we shall use CCW method [9,10,11] to obtain speed of detonation front from other flow variables just behind the front in all the three cases. For converging fronts, the method is to apply the characteristic equation (valid along a negative characteristic) to the flow quantities just behind the front.
Case I: Rm<<1 (Detonation wave in a weakly conducting ideal gas)
Using the flow variables just behind the detonation front, into the characteristic equation (2.8) (keeping in mind that u1 is negative), we obtain
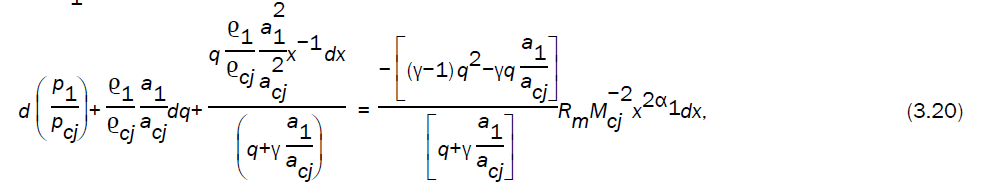
where the magnetic Reynold number Rm is given by
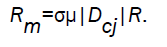
Using the values of flow variables, given by equations (3.9) - (3.12) into the characteristic equation (3.20), we obtain the differential equation between the velocity of the motion of the detonation products and the location of wave front as
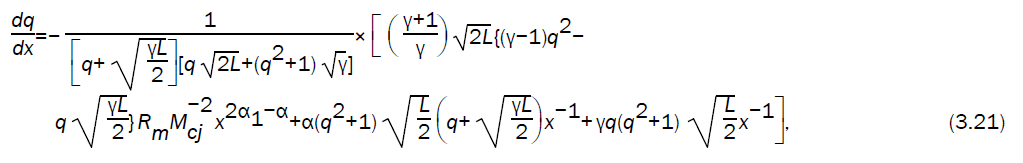
where 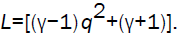
Numerical integration of the differential equation (3.21), alongwith the equations (3.9, 3.10, 3.11) with initial condition q=1, x=1 gives the values of q,  as x decreases from 1 to zero.
as x decreases from 1 to zero.
Case II: Rm>>1 (Pure Magnetogasdynamic Detonation wave)
Using the flow variables just behind the detonation front into the characteristic equation (2.14) (keeping in mind that u1 is negative), we obtain
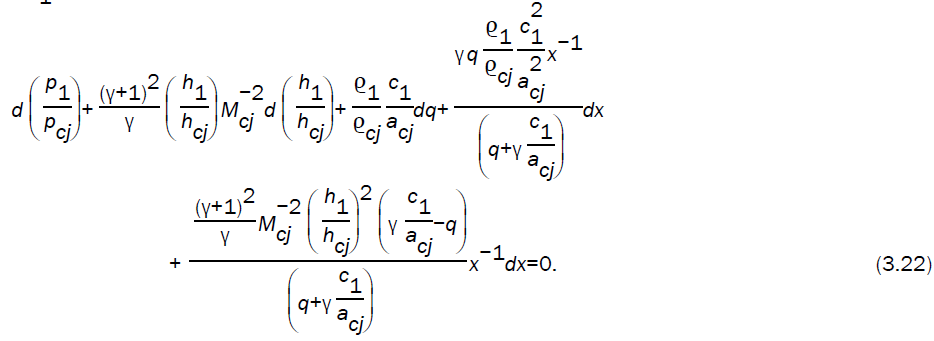
On using the equations (3.14, 3.15, 3.16, 3.17) in equation (3.22), we obtain the following differential equation
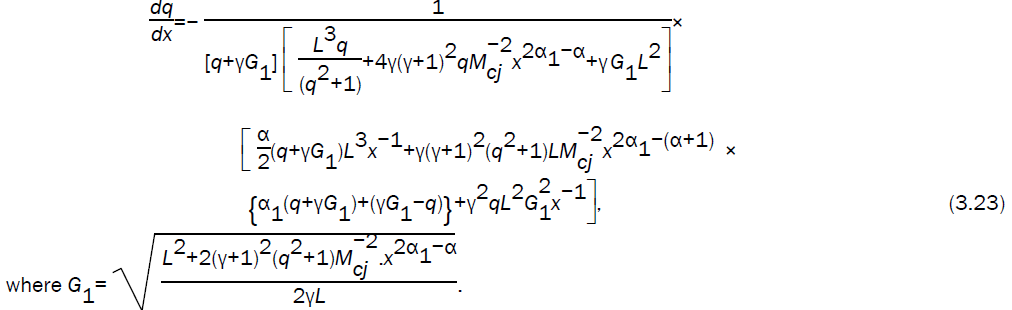
Integrating the differential equation (3.23), numerically and using (3.13) - (3.17) we can obtain 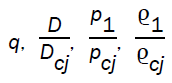 and
and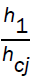 in terms of x.
in terms of x.
Case III: σ:0 → ∞ (Gas-Ionizing Detonation wave)
On using the equations (3.14, 3.15, 3.18, 3.19) in the characteristic equation (2.14) and simplifying, we obtain the differential equation
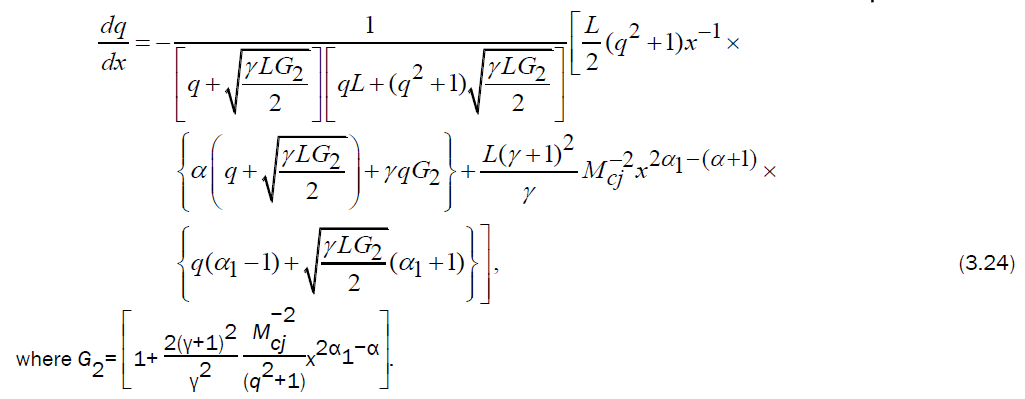
Numerical integration of the differential equation (3.24), and use of equation (3.13, 3.14, 3.15) gives the variation of q, 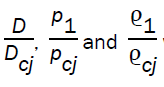 with x.
with x.
For the purpose of numerical calculations, we used the values of 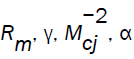 and α1 given by Rm=0.01 (in the case I only); γ = 1.4, 3.0;α1 =−1 and α = 0, 1.
and α1 given by Rm=0.01 (in the case I only); γ = 1.4, 3.0;α1 =−1 and α = 0, 1. 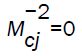 corresponds to the non-magnetic case and α=0 to the case of constant initial density.
corresponds to the non-magnetic case and α=0 to the case of constant initial density.
In the case I, the velocity of detonation front 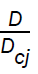 and the pressure behind it
and the pressure behind it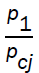 are plotted against the radius x in figures 1 and 2. It is shown that a decrease in the value of index for variable initial density α, accelerates the convergence of the front (figure 1) and increases the pressure behind it (figure 2). A change in the value of the magnetic parameter
are plotted against the radius x in figures 1 and 2. It is shown that a decrease in the value of index for variable initial density α, accelerates the convergence of the front (figure 1) and increases the pressure behind it (figure 2). A change in the value of the magnetic parameter 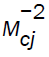 show almost negligible effect on
show almost negligible effect on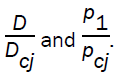 On increasing the value of γ, the velocity of detonation front and the pressure behind it increases near the axis.
On increasing the value of γ, the velocity of detonation front and the pressure behind it increases near the axis.
In the case II, figures 3 and 4 show that an increase in the value of 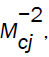 when α=0, decreases the front velocity
when α=0, decreases the front velocity 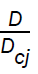 near the axis and also the pressure behind it
near the axis and also the pressure behind it 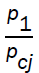 . A decrease in value of α, increases the velocity of detonation front and the pressure behind it in both, the magnetic and non-magnetic cases. An increase in the value of γ in non-magnetic case, rapidly increases the velocity of detonation front and the pressure behind it, whereas in magnetic case, there is a small effect on these variables.
. A decrease in value of α, increases the velocity of detonation front and the pressure behind it in both, the magnetic and non-magnetic cases. An increase in the value of γ in non-magnetic case, rapidly increases the velocity of detonation front and the pressure behind it, whereas in magnetic case, there is a small effect on these variables.
In the case III, figures 5 and 6 show that an increase in the value of 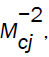 when α=0, decreases the front velocity and the pressure behind it near the axis, and when α = −1, there is a small effect on these variables. On decreasing the value of α, the velocity of detonation front and the pressure behind it increases near the axis. An increase in the value of γ show small effect on the velocity of detonation front, but the pressure behind it increases rapidly.
when α=0, decreases the front velocity and the pressure behind it near the axis, and when α = −1, there is a small effect on these variables. On decreasing the value of α, the velocity of detonation front and the pressure behind it increases near the axis. An increase in the value of γ show small effect on the velocity of detonation front, but the pressure behind it increases rapidly.
In this work we have studied converging cylindrical detonation waves in an ideal gas under the influence of a variable azimuthal magnetic field. The initial density of the medium is assumed to obey a power law.
In case I, on increasing the value of ratio of specific heats (γ), the velocity of detonation front and the pressure behind it increase in both the magnetic and non-magnetic cases. In case II both increase only in the nonmagnetic case.
On increasing the value of 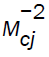 for α=0 and γ = 1.4 in case II, the velocity of detonation front and the pressure behind it decrease. In case III, the velocity of detonation front and the pressure behind it decrease for α = 0 (both for γ = 1.4 and 3.0), on increasing the value of
for α=0 and γ = 1.4 in case II, the velocity of detonation front and the pressure behind it decrease. In case III, the velocity of detonation front and the pressure behind it decrease for α = 0 (both for γ = 1.4 and 3.0), on increasing the value of 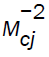 . Thus the presence of azimuthal magnetic field has decaying effect on the convergence of the detonation front.
. Thus the presence of azimuthal magnetic field has decaying effect on the convergence of the detonation front.
In all the three cases, on decreasing the value of α, the velocity of detonation front and the pressure behind it increase near the axis.