ISSN: 2320-2459
ISSN: 2320-2459
1Department of Physics, Kibabii University College, Box 1699, Bungoma-Kenya.
2Department of Physics, Karatina University, Box 1957, Karatina- Kenya.
3Department of Physics, Masinde Muliro University, Box 190, Kakamega-Kenya.
Received date: 07/11/2013; Revised date: 12/12/2013; Accepted date: 17/12/2013
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
The low-temperature energy contributions of a binary K K 41 40 system are studied. The studies are done in both Gross- Pitaevskii (GP) and Thomas-Fermi (TF) approximations. The Gross- Pitaevskii (GP) analysis for K K 41 40 system showed that for positive and negative scattering lengths, the system exhibits positive and negative energies respectively. However, in both cases there is stability of the system away from the centre of the condensate. It was found that the GP energy is the major contributor to the total energy of the K K 41 40 system due to the mean-field interactions. The K K 41 40 system showed a critical condensate radius of about 6 oscillator units at which the system spontaneously moves from the negative attractions to the positive attractions regime where there is more stability against collapse. In the TF approximation, the kinetic energy is not affected by the interaction between the two types of particles. Just as in the GP case, there is also the stability of the system away from the centre of the condensate.
Bosons, fermions, Bose-Einstein condensates (BECs), scattering lengths, oscillator lengths, GP equations, TF equations
The total energy of a macroscopic system is derived from the properties of microscopic constituents of a system [1,2] There are two approaches to the study of statistical mechanics; the independent particle model in isolated systems and the ensemble model involving a large collection of systems. Bosons are atoms with even sum of the number of elementary particles and possess integral spin angular momentum. Fermions are atoms with an odd sum of the number of elementary particles and possess odd half-integral total spin angular momentum.
The origins of Bose-Einstein theory started with Bose [3] and Einstein in 1925. Bose studied photons but
Einstein extended the ideas to atoms, where at low temperatures particles occupy the Zero momentum state
(ZMS). Following the first experimental realization of BEC in a dilute vapour of 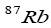 by Wieman and Cornel [4] in 1995, a great deal of experimental and theoretical progress has been made in the field of ultra-cold atomic gases.
Ketterle and Hullet [5] obtained BECs in dilute gases of
by Wieman and Cornel [4] in 1995, a great deal of experimental and theoretical progress has been made in the field of ultra-cold atomic gases.
Ketterle and Hullet [5] obtained BECs in dilute gases of 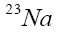 and
and 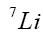 atoms. Trunscott et al [6] reported a binary BEC in
atoms. Trunscott et al [6] reported a binary BEC in 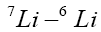 and
and 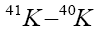 mixtures.
mixtures.
The objectives in this paper are to develop effective mean –field Hamiltonian for bosons, fermions and for a mixture of bosons and fermions on the basis of GP and TF equations. The results of key derivations and analysis of particle and energy distributions are presented. Also the influence of boson-boson and boson-fermion interactions on the stability of Bose-Fermi condensates is studied.
Theoretical Derivations
Gross-Pitaevskii Approximations
In studying BECs upto first order approximation, a non-linear Schrodinger equation also called the GP equation is given as
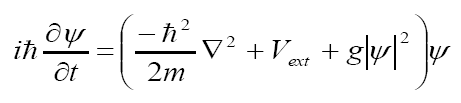 Eq.(1)
Eq.(1)
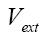 is the external trapping potential and g is a measure of the strength of interaction between the two
types of particles.GP equation has been used to study the groundstate properties of the bosonic component of the
condensates. Roth and Feldmeir [8] modified GP equation to include the mean-field interaction generated by
fermionic cloud. Tripenbach et al studied the structure of binary condensates by numerical simulations of coupled
GPEs.
is the external trapping potential and g is a measure of the strength of interaction between the two
types of particles.GP equation has been used to study the groundstate properties of the bosonic component of the
condensates. Roth and Feldmeir [8] modified GP equation to include the mean-field interaction generated by
fermionic cloud. Tripenbach et al studied the structure of binary condensates by numerical simulations of coupled
GPEs.
Bogoulibouv Approximations
Bogoulibouv approximations were introduced due to the inadequacy of GP equation. It is used to study the non-perturbative interaction between the condensate and the non-condensed atoms. Legget [10,11] showed the relation between the GP and the Bogoulibov approximation.
Microcanonical Ensemble
A microcanonical ensemble model with pair interactions is used. The entropy, Internal energy and specific heat are obtained in terms of the partition function. The distribution of bosons in the j-th energy level is obtained as
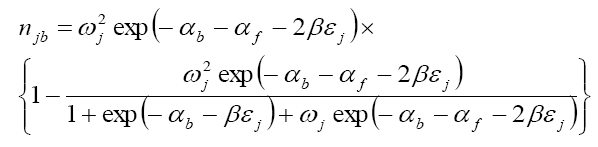 Eq.(2)
Eq.(2)
and for fermions
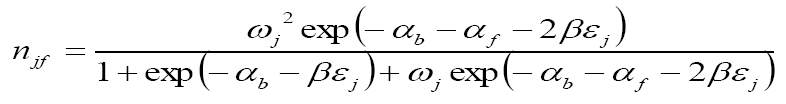 Eq.(3)
Eq.(3)
where 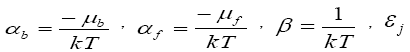 is the energy of the stationary state and
is the energy of the stationary state and 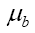 and
and 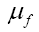 are the
chemical potentials for bosons and fermions, respectively . The partition function, Q, for an ensemble of bosons and fermions is
are the
chemical potentials for bosons and fermions, respectively . The partition function, Q, for an ensemble of bosons and fermions is
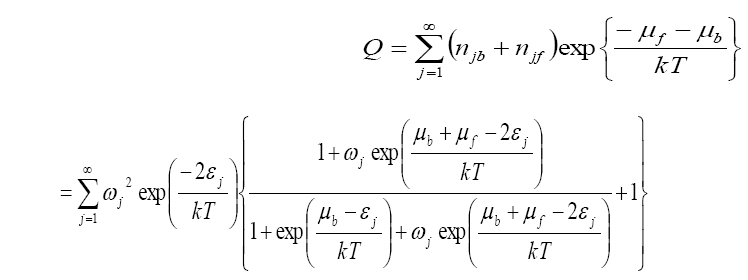 Eq.(4)
Eq.(4)
Entropy, Internal energy and Specific heat are obtained from the standard textbook [1,2] equations
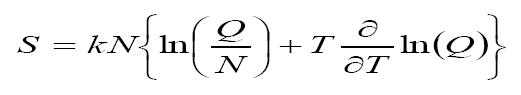 Eq.(5)
Eq.(5)
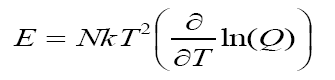 Eq.(6)
Eq.(6)
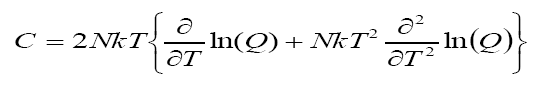 Eq.(7)
Eq.(7)
A mean-field description of two component Bose-Fermi mixture is considered. The time-independent coupled GPEs [13] are written in the standard form for bosons as
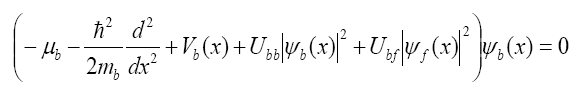 Eq.(8)
Eq.(8)
and for fermions as
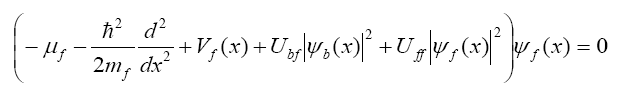 Eq.(9)
Eq.(9)
The boson –fermion and boson-boson interaction strengths are, respectively, defined as
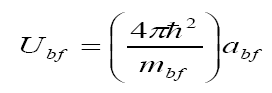 Eq.(10)
Eq.(10)
And
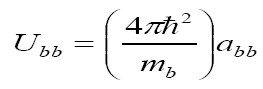 Eq.(11)
Eq.(11)
where 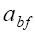 and
and 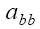 are the boson-fermion and boson-boson s-wave scattering lengths respectively.
are the boson-fermion and boson-boson s-wave scattering lengths respectively.
Total energy of the Bose-Fermi system is obtained from the equation
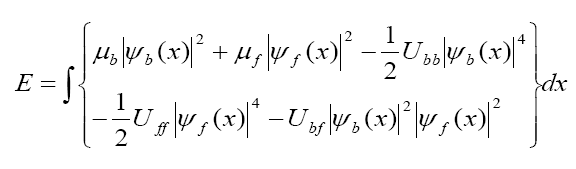 Eq.(12)
Eq.(12)
The commonly used wavefunction in the GP analysis is the one proposed by Legget [8] and is given as
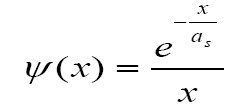 Eq.(13)
Eq.(13)
By using eqs. (8,9,10,11,12 and 13), the total energy for the Bose-Fermi system become
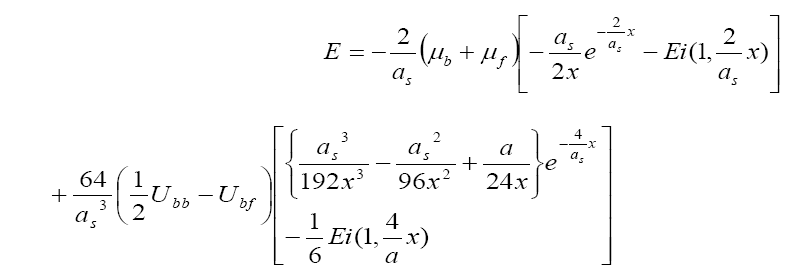 Eq.(14)
Eq.(14)
In eq.(14) Ei is a special function called the Exponential Integral and is defined in standard form as
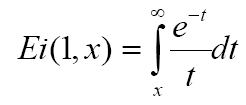 Eq.(15)
Eq.(15)
Thomas-Fermi approximation for a Bose-Fermi system
The particle density for bosons and fermions are, respectively, given as
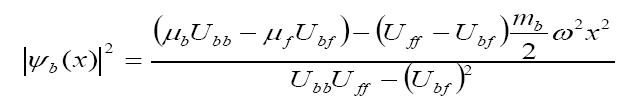 Eq.(16)
Eq.(16)
and
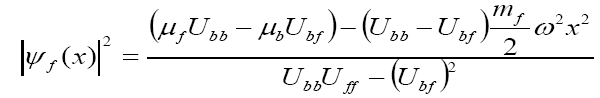 Eq.(17)
Eq.(17)
For partially overlapping wave functions 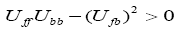 . The combined interactions among fermions
and among bosons is greater than the interactions between bosons and fermions. This is what leads to the
existence of the two types of particles or a partial overlap in the wavefunctions representing the two types of
particles. Similarly the separated wavefunctions would normally occur when
. The combined interactions among fermions
and among bosons is greater than the interactions between bosons and fermions. This is what leads to the
existence of the two types of particles or a partial overlap in the wavefunctions representing the two types of
particles. Similarly the separated wavefunctions would normally occur when 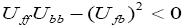 . Here the strength
of the boson-fermion interaction is dominant over boson-boson and fermion-fermion interactions. Consequently this
leads to the separation of the two types of particles or the separation of their wavefunctions. The number of
bosonic and fermionic atoms in each condensate are given, respectively as
. Here the strength
of the boson-fermion interaction is dominant over boson-boson and fermion-fermion interactions. Consequently this
leads to the separation of the two types of particles or the separation of their wavefunctions. The number of
bosonic and fermionic atoms in each condensate are given, respectively as
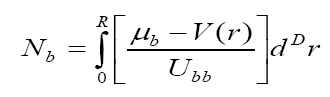 Eq.(18)
Eq.(18)
and
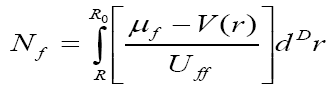 Eq.(19)
Eq.(19)
From eqs. (16,17,18 and 19) the bosonic and fermionic density were again, respectively, obtained as
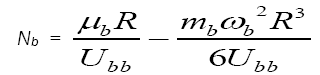 Eq.(20)
Eq.(20)
and
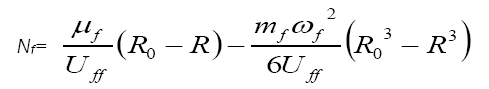 Eq.(21)
Eq.(21)
The eqs. (20 and 21) indicate how the boson and fermion densities vary with the Thomas-Fermi radius R. In eq. (20) the density of bosons has a part with linear dependence on R and a part that has got cubic dependence on R. For all values of R>0, we have a finite density for the bosons within the trap. For R=0, then we have a region in which there are completely no bosons in existence. Similarly eq. (21) shows that the fermionic density has linear dependence with relative Thomas-Fermi radius (R0-R) as well as linear dependence on (R03-R3). Clearly when R=R0 ,then there are no fermions in existence. So fermions would only exist for R < R0. So at the two points when R=0 and R = R0 are the points at which we obtain completely separated regimes for bosons and fermions in the TF approximation.
Stability of boson-fermion mixed condensates
Let us consider the case of a trapped boson-fermion mixed condensate at absolute zero temperature with
positive and negative scattering lengths. In the GP theory we use the boson-order parameter [14] , the Gaussian ansatz  as
as
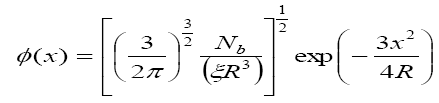 Eq.(22)
Eq.(22)
with 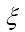 being the oscillator length.
being the oscillator length.
Fermion density distribution is
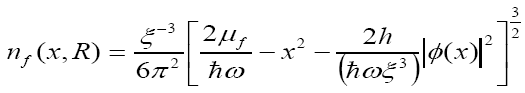 Eq.(23)
Eq.(23)
The total energy was evaluated in terms of the reduced oscillator energy as
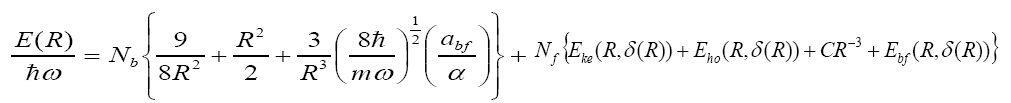 Eq.(24)
Eq.(24)
where α is a measure of the ratio of boson-fermion and boson-boson coupling constants or interaction strengths
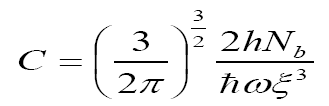 Eq.(25)
Eq.(25)
and
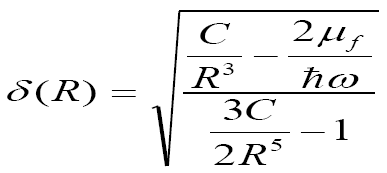 Eq.(26)
Eq.(26)
Analysis
We analyzed eq. (24) for the case of 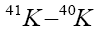 system and obtained the following graph:-
system and obtained the following graph:-
Gross-Pitaevskii energy includes the kinetic energy, harmonic oscillator energy and the boson-fermion interaction energy all calculated in the GP approximation. For the 41K-40K system considered here, the positive scattering length between 41K and 40K atoms implies repulsion between the particles. R being a width of the condensate, we get the result that near the centre of the condensate the interactions are much stronger leading to an almost infinite amount of energy. The system stabilizes as we move away from the centre of the condensate. Stability is usually associated with the lowest energy in the system.
E1 is the kinetic energy, E2 harmonic oscillator energy and E3 is the Bose-Fermi interaction energy in the Thomas-Fermi approximation.
In the Thomas-Fermi approximation and in the low density limit as used in our calculations, the kinetic energy contribution is expected to be large compared to the harmonic oscillator and mean-field contributions. This is because the kinetic energy is not affected by the interaction between the two types of particles. Just as in the Gross-Pitaevskii case, there is also the stability of the system as we move away from the centre of the condensate.
The shape of the graph is almost similar to that obtained in Fig. 5 for the Gross-Pitaevskii energy. This is an indication that the Gross-Pitaevskii energy has a predominant contribution to the total energy. Positive scattering lengths lead to positive energy and also there is stability of the system away from the centre of the condensate.
Next are the results obtained when we consider the negative scattering lengths between the 41K-40K atoms. It is only the Gross-Pitaevskii energies and the corresponding total energies that were evaluated. This was due to the realization that the Thomas-Fermi energies almost remained unaltered even when the sign of the interaction between the bosons and fermions was changed.
In comparison with the result shown in Fig.5, it was realized that by changing the sign of the scattering lengths, the Gross-Pitaevskii energy changed from the positive values to the negative values. Negative scattering lengths results in negative energy. Nevertheless, the stability of the system away from the centre of the condensate was not altered.
The negative scattering lengths also altered the sign of the total energy of the 41K-40K system from positive to negative values. There was a cross over in the total energy at about R= 6.0 oscillator units, which can be referred to as the critical condensate radius. This indicated that in the absence of a positive scattering length (repulsion between the particles), the system can spontaneously move into a regime of positive interactions between the particles.
GP analysis for 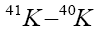 system showed that for positive and negative scattering lengths, the system
exhibits positive and negative energies respectively. However, in both cases there is stability of the system away
from the centre of the condensate. GP energy is the major contributor to the total energy of the
system showed that for positive and negative scattering lengths, the system
exhibits positive and negative energies respectively. However, in both cases there is stability of the system away
from the centre of the condensate. GP energy is the major contributor to the total energy of the 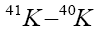 system
due to the mean-field interactions. The
system
due to the mean-field interactions. The 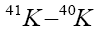 system showed a critical condensate radius of about 6 oscillator units at which the system spontaneously moves from the negative attractions to the positive attractions regime.
system showed a critical condensate radius of about 6 oscillator units at which the system spontaneously moves from the negative attractions to the positive attractions regime.
Thanks to all colleagues in the Department of Physics for intellectual support. A lot of gratitude to the International Centre for Theoretical Physics (ICTP) for allowing us to access their e-journals delivery service.