ISSN: 2320-2459
ISSN: 2320-2459
Department of Physics, The George Washington University, Washington, DC 20052, USA
Received Date: 12/08/2017; Accepted Date: 12/10/2017; Published Date: 17/10/2017
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Suppose in what follows that when and that when and coincide. The final discovery, which we knew all along or should have known all along, following from the constancy of the velocity of light c in the moving system, is that For the time coordinate , this gives which is equivalent to the Lorentz transformation for the time coordinate . In the final blow to Einstein’s theory, for the rod moving to the left, with velocity , and x positive, we have Clearly Contradicting the experimentally verified slower clock in the moving system.
Magnetic Nanoparticles (MNPs), Nanoparticles (NPs), Relaxation time, Critical size, Blocking temperature
As in the consideration, in which we belatedly discover that the parallel and perpendicular arms of the apparatus are clocks, of the Michelson-Morley experiment, we find that two synchronous clocks define the light clock between them. Given two points, A and B, with synchronous clocks at A and B, we have:
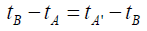
For a light ray leaving A at time tA, reflected at B at time tB, and returning to A at time tA'. We may as well assume that tA=0, so that:
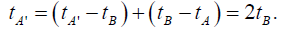
For these points and clocks in the rest system and l the distance between A and B, we have:
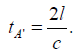
If, on the other hand, these points and clocks are in the moving, with velocity u, system, by various arguments, the same equation, rewritten, identically, as:
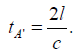
holds.
By Einstein’s second postulate, we can obtain this result, but we have previously shown that the second postulate is false. By not assuming it here, and subsequently showing that it is false, we avoid the unnecessary step of assuming it to be true and we show that the equation holds any way [1-5].
In the moving system, measuring rods and lengths to be measured change, from the rest system to the moving one, by the same factor; clocks and clock periods behave in the same way. By the principle of relativity, Einstein concludes the length to be discovered by operation (a) — “The observer moves together with the given measuring-rod, and measures the length of the rod directly by superposing the measuring-rod, in just the same way as if all three were at rest.” — “we will call it ‘the length of the rod in the moving system’—must be equal to the length l of the stationary rod.” We, on the other hand, arrive at this result, and the corresponding one involving clocks and clock period analytically, by reflecting that the measuring instrument and that which is to be measured change by the same factor, which depends on the case.
Einstein’s “Principle of Relativity,” that “…the same laws of electro dynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good”, suggests that the equations of mechanics hold in certain, possibly the empty set, frames of reference. This suggestion evidently applies to the system moving with a constant velocity u and the equation that the length of the rod in the moving system equals its measured value, which is l, the same value obtained if the rod is in the rest system; yet, there is no conceivable application of this principle or postulate to this case [6-8].
The experimental, thought experiments included, result for the length, as measured by measuring rods in the rest system, of a rod, oriented lengthwise, parallel to the direction of motion, in the moving system is that:
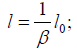
The result for the period, as measured by clocks in the rest system, of a clock in the moving system is that:
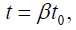
Where, in each case,
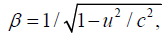
And 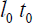 are the measured values in the rest system for the rod and clock in the rest system. In the case of the light clock
between two points A and B, with synchronous clocks at A and B, its period is the time:
are the measured values in the rest system for the rod and clock in the rest system. In the case of the light clock
between two points A and B, with synchronous clocks at A and B, its period is the time:
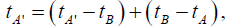
The natural unit of time for this clock.
Since clocks in the moving system move more slowly than clocks in the rest system by the factor 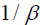 , the period, as
measured in the moving system, of a clock in the moving system, is
, the period, as
measured in the moving system, of a clock in the moving system, is 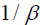 times the value as measured in the rest system; thus,
times the value as measured in the rest system; thus,
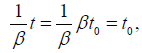
Which is the same value as the period of the clock in the rest system as measured in the rest system [9-11].
Similarly, since the length as measured in the moving system of a rod, oriented lengthwise, parallel to the direction of motion, in the moving system is greater, by a factor of β, than the length of the rod as measured in the rest system, we have:
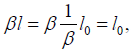
Which the same value as the length of the rod is in the rest system as measured in the rest system.
Thus, for a light clock, oriented lengthwise, parallel to the direction of motion, in the moving system, the average velocity, round-trip, as measured in the moving system, of the light is just c, the same value for this velocity as measured in the rest system for the same light clock at rest in the rest system; we have,
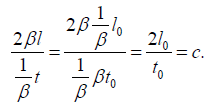
The one-directional velocity, as we showed in The Material Point Universe Revisited, as measured in the moving system, of light in the light clock so-oriented is not c. For light moving in the opposite direction as the moving rod, we have, as measured in the rest system,
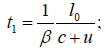
for light moving in the same direction as the moving rod, we have, as measured in the rest system,
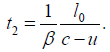
Thus, as measured in the rest system, the period of the moving light clock is just:
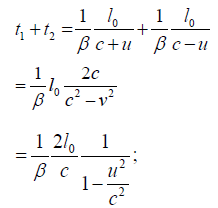
thus, as measured in the moving system, where the clocks move more slowly by the factor 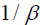 . this period is:
. this period is:
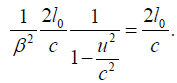
In the moving system, for light moving in the opposite direction as the moving rod, we have for the velocity:
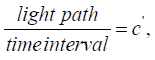
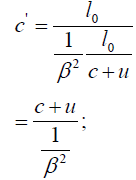
for light moving in the same direction as the moving rod, we have:
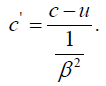
In measuring the average velocity of light in the parallel light clock, we only need one clock, the one at the endpoint where the light begins. For the period in the moving system, we have,
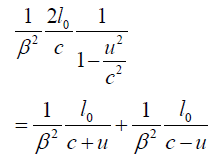
This allows us to consider the times, corresponding to t1 and t2 , in the moving system as 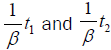 .
.
This analysis is correct provided we have made no errors in assumptions or logic; in effect, it is a conditional proof. Einstein assumes, via the second postulate, that the velocity of light is c. To derive the equations of the Lorentz transformation, Einstein assumes that clocks in the moving system are synchronous. For the period, as measured in the moving system, of the light clock, parallel to the direction of motion, determined by two synchronous clocks at points A and B in the moving system, we have:
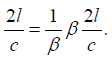
Since clocks in the moving system move more slowly by the factor 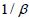 , the period of this clock as measured in the rest
system is:
, the period of this clock as measured in the rest
system is:
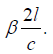
Thus, this clock in the moving system has a period which is greater, by a factor of β, than the period as measured in the rest system of the same clock at rest in the rest system. Here, we have used the result, of what Einstein calls operation (a), that the measurement, in the moving system, of the length of a rod in the moving system is the same as the measurement, in the rest system, of the length of the same rod at rest in the rest system.
Since, by assumption, clocks in the moving system are synchronous, the time in each direction for light to travel from A to B or B to A must be:
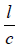
in the moving system; in the rest system,
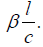
Thus, as viewed in the rest system, the parallel light clock has length, by the Lorentz contraction,
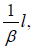
and does not move with velocity u. In order that the parallel light clock slow down by a factor of:
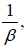
The light in the parallel light clock must slow down by a factor of:
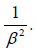
Thus, we obtain two contradictions, the second of which is that the light in the parallel light clock must slow down by a factor of:
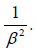
That clocks in the moving system move more slowly by the factor 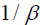 follows from the assumption of synchronous clocks
and the second postulate. Given a clock at the point A and a point
follows from the assumption of synchronous clocks
and the second postulate. Given a clock at the point A and a point 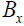 a distance X from A, a clock at
a distance X from A, a clock at 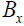 synchronous with the
one at A must read:
synchronous with the
one at A must read:
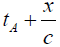
When a light ray, emitted at A at time 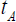 , reaches
, reaches 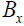 . Since
. Since 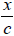 is the time, according to the clock at A, for the light to reach
is the time, according to the clock at A, for the light to reach 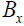 , this extends the clock at A to any point
, this extends the clock at A to any point 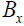 . By the second postulate, the time for light to travel from
. By the second postulate, the time for light to travel from 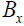 to A is also
to A is also 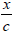 and,
hence, the clocks are synchronous.
and,
hence, the clocks are synchronous.
In deriving the equations of the Lorentz transformation, Einstein assumes that clocks in the moving system are synchronous,
but he footnotes that “the equations of the Lorentz transformation may be more simply deduced directly from the condition
that in virtue of those equations the relation 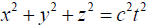 shall have as its consequence the second relation
shall have as its consequence the second relation 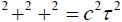 .” Illogically, this suggests that p is true if
.” Illogically, this suggests that p is true if 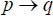 is true and q is true, where p is the assertion that the equations
of the Lorentz transformation hold and q is the assertion that the relation
is true and q is true, where p is the assertion that the equations
of the Lorentz transformation hold and q is the assertion that the relation 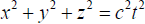 shall have as its consequence the
second relation
shall have as its consequence the
second relation 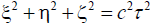 .
.
Nevertheless, armed with the assumption of synchronous clocks and the, evidently, equivalent, assumption of the second postulate, Einstein derives the equations, which are good for giving coordinates in the moving system such that the second postulate is true, of the Lorentz transformation.
We have proved, contradicting the second postulate, that the velocity of light as measured in the moving system is not c; this, in turn, implies that the equations of the Lorentz transformation are false.
The experimental result for the velocity of light in the parallel direction in the moving system is obtained by multiplying the experimental value of the wavelength by the experimental value, given by the Doppler. Effect, of the frequency, the value so obtained, if the light is moving in the direction of the moving system, is:
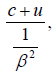
the result we obtained by analysis. The evidence thus contradicts Einstein’s second postulate and, hence, the equations of the Lorentz transformation.
If the evidence contradicts the Einstein’s theory, then the theory is false. There are no experiments that obtain the value c for the velocity of light in the moving system. Even if the proponents of relativity were to give valid arguments that contradict the analysis that we offer here, Einstein’s theory is false because of the evidence. The analysis, which is the correct one, is false only if there is a false assumption or there is a logical error.
Richard Sonnenfeld’s claim that we must be wrong because the theory has been proved is false because the theory is false. James Binney’s claim that contradictions are to be expected because we stepped outside of Einstein’s framework puts the framework, which Binney does not define, as non-falsifiable since considering the framework itself is not permissible.
Further consideration of the equations of the Lorentz transformation is not necessary, but the equations cannot by our analysis be true: something must be wrong with the equations. In the case of the distance coordinate along the direction of motion, the equation is:
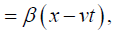
where ξ is the distance coordinate in the moving system. In Einstein’s derivation of the equation’s of the Lorentz transformation, the distance coordinate x ' of a point at rest in the moving system k along the direction of motion is given by:
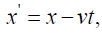
where x is the coordinate of the moving point in the rest system:
“. . . it is clear that a point at rest in the system k must have a system of values x', y, z independent of time.” He sets out to define τ as a function of x', y, z, and t, noting that “we have to express in equations that τ is nothing else than the summary of data of clocks at rest in system k, which have been synchronized according to the rule given in § 1.”
Einstein’s use, in the expression, a point at rest in the system k, of the phrase, at rest, turns for him the coordinate of a point at rest in the moving system k into the coordinate of a point in the rest system. The coordinate x' is not the coordinate of a point in the moving system k since it does not move; hence it is not the coordinate of a point at rest in the moving system either. In stating that x' is the coordinate of a point at rest in the moving system k, Einstein makes a false statement, which allows him to consider x' as both the coordinate of a point in the rest system and the coordinate of a point in the moving system k without stating this.
At face value, the expression,
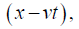
gives the rest system coordinate x' of a point in the moving system when 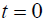 .
.
Since lengths in the moving system are Lorentz contracted by a factor of 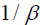 , the coordinate x ' is, assuming the origin
of the distance coordinates of the rest system and the moving system coincide when
, the coordinate x ' is, assuming the origin
of the distance coordinates of the rest system and the moving system coincide when 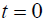 ,
, 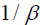 times the length x '' of the
measuring rod, which when placed in the moving system the right endpoint of which is x ' and the left endpoint of which is 0, in
the rest system. Thus:
times the length x '' of the
measuring rod, which when placed in the moving system the right endpoint of which is x ' and the left endpoint of which is 0, in
the rest system. Thus:
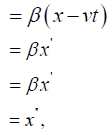
and the length of the moving measuring rod in the distance coordinate of the moving system is just the length of the measuring rod at rest in the rest system.
For the time coordinate τ in the moving system, the Lorentz transformation from the time coordinate t in the rest system is given by:
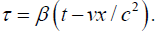
Einstein’s clock in k, expressing “in equations that τ is nothing else than the summary of data of clocks at rest in system k, which have been synchronized according to the rule given in § 1,” is just the clock with period one half the period of the light clock between two synchronous clocks:
“From the origin of system k let a ray be emitted at the time Τ0 along the X-axis to x', and at the time Τ1 be reflected thence to
the origin of the co-ordinates, arriving there at time Τ2; we must then have 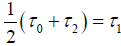 , or, by inserting the arguments of the
function τ and applying the principle of the constancy of the velocity of light in the stationary system :
, or, by inserting the arguments of the
function τ and applying the principle of the constancy of the velocity of light in the stationary system :
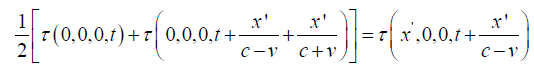
The ordered quadruple (x,y,z,t), with each coordinate in the stationary system K, has X-coordinate x' for the point the light ray reaches along the X-axis. It should be apparent, by looking at the X-coordinate x and the time coordinate t, that Einstein considers a point at rest in the system k to be both in the moving system and the rest system. We note this confusion, which amounts to a logical error; here if only to point out that we caught it. A second confusion lies in that there are two rest systems.
Ironically, in the same way, clocks in the moving system become clocks in the rest system since, distance-coordinate wise, the rest system is obtained by subtracting vt from a point x in the moving system as measured in the rest system. On the other hand, it should be clear that Einstein’s t gives the time according to clocks in the rest system K.
Now, suppose that clocks in the moving system are synchronous and that clocks in the rest system have the same property.
Suppose further that 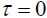 when
when 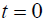 . Since clocks in the moving system move more slowly by a factor of
. Since clocks in the moving system move more slowly by a factor of 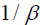 , we have:
, we have:
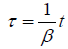
This last expression, intentionally bold, for τ is independent of x.
For the parallel light clock between two synchronous clocks in the moving system, the times 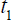 and
and 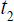 in the moving system
are just what we obtained previously:
in the moving system
are just what we obtained previously:
For light moving in the opposite direction as the moving rod, we have, as measured in the rest system,
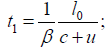
for light moving in the same direction as the moving rod, we have, as measured in the rest system,
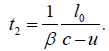
For the corresponding times in the moving system, simply multiply these times by 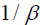 ; the resulting times in the moving
system are not equal contradicting the assumption that clocks in the moving system are synchronous.
; the resulting times in the moving
system are not equal contradicting the assumption that clocks in the moving system are synchronous.
Now, to indicate where we are going with this, no matter how flawed Einstein’s derivation of the equations of the Lorentz transformation, the equations themselves are false. When Einstein needs to show that:
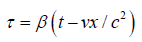
gives a slower clock in the moving system, he sets 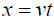 , so that:
, so that:
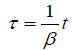
which, of course, is the same, just given, equation that contradicts the assumption that clocks in the moving system are synchronous.
If the hilarity of the situation were not obvious, Einstein has two equations, one of which is the Lorentz transformation, good for showing that the velocity of light in the moving system is c, for the time coordinate and the other of which, obtained from the Lorentz transformation as described, good for demonstrating a slower clock.
The last equation, obtained by setting 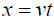 , holds when the latter condition is met; whereas, the previous, identical
equation, holds for all x. By Einstein’s setup, where τ is the time in k for a light ray emitted at time
, holds when the latter condition is met; whereas, the previous, identical
equation, holds for all x. By Einstein’s setup, where τ is the time in k for a light ray emitted at time 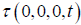 to travel to x',
to travel to x',
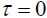
if t=0 and 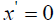 . Thus, Einstein’s result does not give a slower clock. Even if
. Thus, Einstein’s result does not give a slower clock. Even if 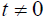 when the light ray is emitted from
when the light ray is emitted from 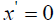 , Τ has the same value at
, Τ has the same value at 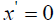 as when it left
as when it left 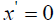 .
.
If we try to ignore Einstein’s setup and argue that the equations of the Lorentz transformation hold, Einstein’s setup follows from the definition of x and the assumption that clocks in the moving system are synchronous. After all, Einstein’s clock in k expresses “in equations that τ is nothing else than the summary of data of clocks at rest in system k, which have been synchronized according to the rule given in § 1.”
Suppose in what follows that 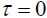 when
when 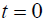 and that
and that 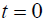 when
when 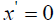 and
and 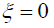 coincide.
coincide.
The final discovery, which we knew all along or should have known all along, following from the constancy of the velocity of light c in the moving system, is that:
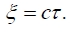
We have:
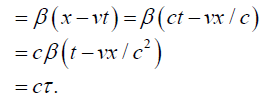
Thus, working backwards,
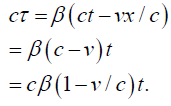
This gives:
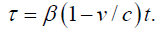
When we re-examined the Bender’s Rods example in Bender Goes to Oxford to see how Michael Bowler evaluates ξ and τ to show, when he needed to show that the times, for light to go from one end of each rod to the other, were equal, that the velocity of light is c in each case, we find that Bowler unnecessarily replaces x and t by their respective values, Remarking, “This is getting monotonous but I may as well finish up,” Bowler nevertheless calculates ξ and τ for “Event 4 is where the light pulse emitted in event 1 catches up the right hand end of the right moving rod,” obtaining unwieldy expressions to show that:
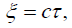
which we already knew.
In the final blow to Einstein’s theory, for the rod moving to the left, with velocity –v , and x positive, we have:
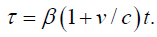
Clearly,
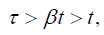
contradicting the experimentally verified slower clock in the moving system.
Bowler’s calculation for light reaching the right endpoint of the left moving rod, obtaining:
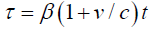
for 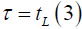 and
and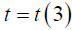 , is as follows:
, is as follows:
“Event number 3 is light launched at event 1 reaching the right hand end of the left moving rod. First work out the coordinates in frame S.
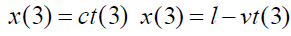
because the right hand end of the rod at rest in 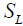 has moved to the left by
has moved to the left by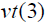 when it meets the oncoming light pulse.
Solve to obtain:
when it meets the oncoming light pulse.
Solve to obtain:
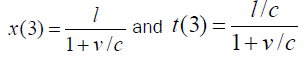
and of course light has travelled at speed c between event 1 and event 3 as measured in S.
Now calculate the coordinates measured in 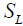 for event 3, by substitution of
for event 3, by substitution of 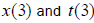 into the transformations from
S to
into the transformations from
S to 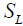 :
:
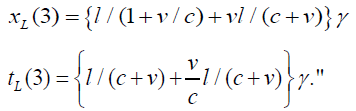
We began by considering the light clock between two synchronous clocks and found that:
1. The clock at A determines the time of all clocks that are synchronous with it. And,
2. The time of the clock at the point A is extended to all points with clocks synchronous with the clock at A.
For the measured velocity of light in the moving system, we obtain:
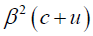
if the light is moving toward the system and:
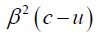
if the light is moving away from the system.
We have proved, contradicting the second postulate, that the velocity of light as measured in the moving system is not c; this, in turn, implies that the equations of the Lorentz transformation are false.
The experimental result for the velocity of light in the parallel direction in the moving system is obtained by multiplying the experimental value of the wavelength by the experimental value, given by the Doppler effect, of the frequency. The value so obtained, if the light is moving in the direction of the moving system, is:
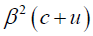 ,
,
the result we obtained by analysis. The evidence thus contradicts Einstein’s second postulate and, hence, the equations of the Lorentz transformation.
No matter how flawed Einstein’s derivation of the equations of the Lorentz transformation, the equations themselves are false. When Einstein needs to show that:
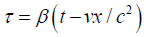
gives a slower clock in the moving system, he sets 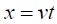 , so that:
, so that:
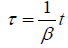
The last equation, obtained by setting 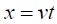 , holds when the latter condition is met; whereas, the previous, identical
equation, holds for all x. By Einstein’s setup, where τ is the time in k for a light ray emitted at time
, holds when the latter condition is met; whereas, the previous, identical
equation, holds for all x. By Einstein’s setup, where τ is the time in k for a light ray emitted at time 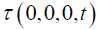 to travel to
to travel to 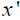 ,
,
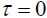
if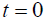 and
and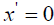 . Thus, Einstein’s result does not give a slower clock. Even if
. Thus, Einstein’s result does not give a slower clock. Even if 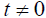 when the light ray is emitted from
when the light ray is emitted from 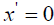 , τ has the same value at
, τ has the same value at 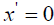 as when it left
as when it left 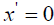 .
.
Finally, as stated in the abstract, we argue as follows:
Suppose in what follows that 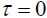 when
when 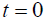 and that
and that 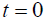 when
when 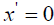 and
and 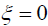 coincide.
coincide.
The final discovery, which we knew all along or should have known all along, following from the constancy of the velocity of light c in the moving system, is that:
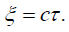
For the time coordinate τ, this gives:
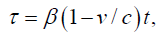
which is equivalent to the Lorentz transformation for the time coordinate τ.
In the final blow to Einstein’s theory, for the rod moving to the left, with velocity –v, and x positive, we have:
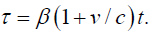
Clearly,
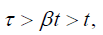
Contradicting the experimentally verified slower clock in the moving system.
Conclusion: the final blow. Of the handful of ways that we show that the second postulate and the equation for the time coordinate of the Lorentz transformation are false, the last argument follows directly from the second postulate and the equation for the time coordinate of the Lorentz transformation.
Thus, in a blow to James Binney’s claim that we step outside the framework, we clearly do not. The argument that we are incorrect because Einstein’s theories have been proved is false because we just proved, here and elsewhere, that the theory is false. The argument that since all the great minds have looked at Einstein’s theories and found them to be true, the theories are true is false since we just proved, here and elsewhere, the theories to be false. The great minds are phony and so is the theory.