ISSN: 2320-2459
ISSN: 2320-2459
Tohid Sedghi1*, Yashar Zehforoosh1 and Mahdi Jalali2
1Department of Electrical Engineering, Urmia Branch, Islamic Azad University, Urmia, Iran.
2Department of Electrical Engineering, Naghadeh Branch, Islamic Azad University, Naghadeh, Iran.
Received date: 03/01/2013 Revised date: 27/03/2013 Accepted date: 10/04/2013
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
This paper is a preliminary study of None-Stationary Transformed signals viewed as Fusioned nonlinear dynamical remote sensing systems. A class of recursively defined None-Stationary Transformed signals is introduced, and one specific signal is considered. It will be shown that such None-Stationary Transformed signals can exhibit complex dynamics in phase space. This means that they experience sensitive dependence on initial conditions. Using the spread multi Spectral spectrum, we determine the stability of this signal. We will also investigate whether such signal is of practical use in remote sensing by examining its ambiguity functions
Ambiguity, Function, Multi Spectral Spectrum, Remote Sensing,
Fusion, Telemetry, Spatial, spectral information.
This paper is a preliminary investigation of a class of remote sensing None-Stationary transformed signals generated by Fusion defined functions. None-Stationary Transformed signals are of fundamental importance in remote sensing, since a remote sensing system uses transmitted and returned None-Stationary Transformed signals from the environment to decide on the presence of signal, as well as their range, bearing and speed. The issue of an appropriate choice of signal is complex, and application dependent. There are many types of None-Stationary Transformed signals, including linear frequency modulation (LFM), pseudorandom codes, step frequency continuous waves, step frequency pulse trains, single frequency pulse trains and random noise. This paper is a brief examination of a new generation and new class of None-Stationary Transformed signals, known as None-Stationary Transformed signals. Such None-Stationary Transformed signals may be of importance in remote sensing for a number of reasons. The first is that they are generated from a deterministic map, but can be made to appear as noise. This would be useful from an electronic protection point of view. Secondly, since these None-Stationary Transformed signals can be generated from a single dynamical system, with different control parameters and initial conditions, it may be possible to reduce the need for a comprehensive library of None-Stationary Transformed signals in a remote sensing system. The generation of such None-Stationary Transformed signals, as a discrete time dynamical system (DDS), will be outlined. We investigate the stability of such None-Stationary Transformed signals, using the Remote sensing multi Spectral spectrum.
The purpose of this paper is to consider a class of Fusion defined None-Stationary Transformed signals that exhibit complex dynamics in phase space. This work arose out of an interesting remote sensing signal in [1]. This signal exhibits sensitive dependence on initial conditions, and has an unusual self replicating feature in phase space. The main issue to be addressed in this paper is whether such None-Stationary Transformed signals are of practical use in remote sensing. None-Stationary Transformed signals are of paramount importance in remote sensing. Remote sensing systems use different types of None-Stationary Transformed signals for specific applications in varying situational contexts [2]. There are hence many different classes of remote sensing None-Stationary Transformed signals[2] describes four classes of remote sensing None-Stationary Transformed signals, based upon their characteristics and ambiguity functions. Linear frequency modulation, single frequency pulse trains, step frequency continuous waves, step frequency pulse trains, pseudorandom codes and random noise are examples pointed out in [3]. Relatively new classes of None-stationary transformed signals are those which have None-Stationary dynamics [3,4]. Such a class of None-Stationary Transformed signals exhibits a phenomenon known as sensitive dependence on initial conditions. A None-Stationary dynamical system is a nonlinear dynamical system whose output has sensitive dependence on initial conditions. Chaos theory is the analysis of the behavior of such systems. As such, chaos theory is not really a theory of chaos, but is more concerned with understanding the complex behavior of nonlinear dynamical systems. We will introduce briefly the study of such systems, and in particular, will be interested in determining under what conditions such a system becomes None-Stationary. A class of remote sensing None-Stationary Transformed signals will be introduced. We will investigate one signal in this class, and apply the ambiguity function to see whether they are of practical use in remote sensing [5,6].
Let S be the class of all real-valued remote sensing None-Stationary Transformed signals, including both those defined on a discrete and continuous time domain. In order to motivate the work to follow, we consider a subclass of S that can be defined through a dynamical system. Assume 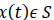 , is continuous and differentiable within a domain. From a physical point of view, the derivative of this signal, dx(t)/dt, is the rate of change of it in a propagating medium. We may hence analysis the signal via this rate of change, so assume that
, is continuous and differentiable within a domain. From a physical point of view, the derivative of this signal, dx(t)/dt, is the rate of change of it in a propagating medium. We may hence analysis the signal via this rate of change, so assume that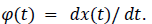 In addition to this, we may assume that in some cases, φ(t) can be expressed as a nonlinear composition of the signal x(t). Thus, there may exist a function ψ such that
In addition to this, we may assume that in some cases, φ(t) can be expressed as a nonlinear composition of the signal x(t). Thus, there may exist a function ψ such that 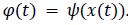 Hence, equivalently,
Hence, equivalently, 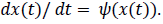 To show this class of None-Stationary Transformed signals is nonempty, consider the signal
To show this class of None-Stationary Transformed signals is nonempty, consider the signal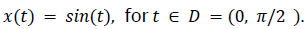 Its derivative is
Its derivative is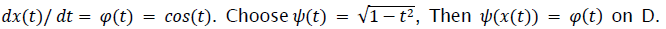 Hence, we can define the class of None-Stationary Transformed signals
Hence, we can define the class of None-Stationary Transformed signals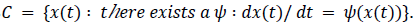 As in [10], we can consider fusioned time, since None-Stationary Transformed signals are often fusioned so they can be processed by digital computers.
As in [10], we can consider fusioned time, since None-Stationary Transformed signals are often fusioned so they can be processed by digital computers.
Hence we can further restrict attention to the subclass 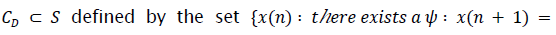
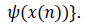
The function Ψ defined in the set CD will be referred to as a generator of a signal. We specialize the discussion to one dimensional discrete maps, since we will be exclusively studying None-Stationary Transformed signals from the class CD. A dynamical system is a physical system which is described by a deterministic set of rules that change with time. Suppose the variables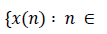 IN} describe the states of the system at each discrete time point n. Then we assume there is a generator function Ψ ,defined on the range of x(n), such that :
IN} describe the states of the system at each discrete time point n. Then we assume there is a generator function Ψ ,defined on the range of x(n), such that :
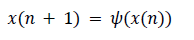 (1)
(1)
The generator Ψ in (Eq.1) determines the evolution of the system, and in general will be nonlinear. We refer to the system’s state space as the fusion space M where the functions x(n) take values. In the context of the discrete None-Stationary Transformed signals considered here, the state fusion space will be subsets of the real line. As an example, the well-known Logistic Map has generator 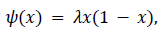 and the corresponding map, defined through (1) has initial value
and the corresponding map, defined through (1) has initial value  We will show that this map becomes unstable as λ changes, using its Remote sensing multi Spectral spectrum. It is not difficult to write down the general solution to (1). Let
We will show that this map becomes unstable as λ changes, using its Remote sensing multi Spectral spectrum. It is not difficult to write down the general solution to (1). Let 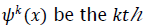 composition of Ψ with itself. By a simple recursion, it is not difficult to show that is the solution to (Eq.1).
composition of Ψ with itself. By a simple recursion, it is not difficult to show that is the solution to (Eq.1).

The path in the state fusion space that a dynamical system, defined through (Eq.2) , traces out is called its trajectory or orbit. A dissipative dynamical system is characterized by convergence of trajectories in its state fusion space. An attractor is defined to be a set of points to which all neighboring trajectories converge in phase fusion space. The attractor set consists of all limit points of the discrete map defined by (Eq.1). A point attractor is a single point to which trajectories converge, also known as a stable fixed point. A dynamical system may have a set of points which are visited periodically. Such points are referred to as a stable limit cycle, with periodic orbits. An attractor is also an invariant set, meaning that when a trajectory starts in it, it remains in the set forever. The largest subset of an attractor set, consisting of the largest set of points to which all nearby orbits converge, is called the basin of attraction. In a nonlinear dynamical system, where orbits in an attractor move apart with increasing time, the system is said to possess a strange attractor. Such dynamical systems are referred to as being none-Stationary. Chaos is often defined to be the a periodic long run behavior in a deterministic dynamical system that exhibits sensitive dependence on initial conditions. There are three so-called signatures of chaos:
a) Aperiodicity in limiting behavior, meaning that the fusion system does not converge to a single point as discrete time increases without bound;
b) It is a deterministic fusion system, with no stochastic component, but is nonlinear;
c) The fusion system exhibits sensitive dependence on initial conditions, meaning arbitrarily close trajectories will diverge apart exponentially fast.
This multi Spectral spectrum is invariant in a basin of attraction, and so will only vary in different regions of stability. In the current case, the signal is entirely None-Stationary, and then undergoes periodic transitions from chaos to stability, as λ increases. Fig. 1 is a plot of the signal as a function of λ. In the plot, λ ranges from 0.1 to 2, in increments of 0.001. The starting value for each iteration is x(0)=2. For each λ iterations have been used to generate each point of the signal. The plot shows the stability of the solution as a function of λ, and then its transition to unstable and None-Stationary behavior. An interesting feature of the transition to that the signal has a single stable solution, which evolves to a cone-like structure. A closer examination of the plot shows this behavior occurs frequently. Fig. 2 contains a number of plots of the absolute value of the ambiguity function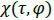 for this signal, with λ = 2. Note that the signal under consideration is defined in terms of discrete time, and consequently the plot does not have the same resolution. The first two plots show the magnitude of the function, in
for this signal, with λ = 2. Note that the signal under consideration is defined in terms of discrete time, and consequently the plot does not have the same resolution. The first two plots show the magnitude of the function, in 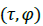 fusion space, using color-contour plots. The third plot shows the function
fusion space, using color-contour plots. The third plot shows the function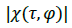 as a surface in Fusion fusion space. The final plot shows the absolute value of the normalised auto correlation function :
as a surface in Fusion fusion space. The final plot shows the absolute value of the normalised auto correlation function :
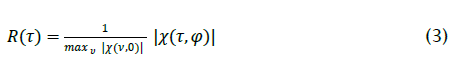
The scale used for τ is discrete time units, while φ is in radians. The autocorrelation plot is over a larger range of values of τ in contrast to the three other plots. The ambiguity function in this case is almost a spike at the origin, with ripples of volume spread out from the origin  =(0,0). Reference [2] class such None-Stationary Transformed signals as irregular or noise-like. Such None-Stationary Transformed signals are a periodic and uncorrelated with themselves except on small intervals. The aperiodicity of the signal under consideration is inherently related to its None-Stationary nature.
=(0,0). Reference [2] class such None-Stationary Transformed signals as irregular or noise-like. Such None-Stationary Transformed signals are a periodic and uncorrelated with themselves except on small intervals. The aperiodicity of the signal under consideration is inherently related to its None-Stationary nature.
Fig.2 shows it has the expected autocorrelation property. Due to the shape of the ambiguity functions in Fig.2, the corresponding signal should have an ability to resolve signal in both time delay and Fusion space shift. However, it would be expected that such a signal may not provide a remote sensing with a sufficient ability to differentiate signal in noisy with a low Remote sensing Cross Section (RCS), due to the extensive high side-transform response in the ambiguity function.
We describe the plots from the top down. The first plot shows the absolute value of the ambiguity function’s concentration in terms of a color multi Spectral spectrum. The second plot shows a colored contour version of the first. The third plot shows the absolute value of the ambiguity function as a surface in fusion space. Finally, the fourth plot shows the normalized autocorrelation function. Since the corresponding signal is in discrete time, the time delay , (τ ) axis values are in discrete time units. Better graphical resolution is achieved by extending this axis. The Fusion space axis is in units of radians, while the time delay is measured in seconds. The absolute value of the ambiguity function is in a linear scale. The autocorrelation plot is shown over a larger multi Spectral spectrum of values of τ than used in the previous three subplots, and also is in a linear scale.
Figure 3: Ambiguity function plots for the signal with generator as in Fig.1, except the plots are over larger time delay and Fusion space shift intervals. The top plot is of the absolute value of the ambiguity function, again as a surface, while the second plot shows the contours and corresponding ambiguity function values using a color bar. The ambiguity function is in a linear scale.
Their stability was analyzed using a multi Spectral spectrum. These None-Stationary Transformed signals are members of a class of irregular/noise like None-Stationary Transformed signals described in [2]. Based upon the shape of the absolute value of their ambiguity functions, we can conclude that they should have an ability to resolve signal in both time delay and Fusion space shift. The disadvantage of such None-Stationary Transformed signals is that they have relatively high range and Fusion space side transforms in the ambiguity diagram, which will limit their ability to discriminate small signal against noisy and small signal in the vicinity of larger signal.
This paper is the result of a research project approved by research committee at Islamic Azad University, Urmia Branch, Urmia, Iran.