Magneto-Electric Effect and Topological Insulators

Opinion

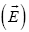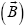The end of the 19^th century marked the birth of an interesting phenomenon in which an applied electric field was able to induce magnetization and an applied magnetic field was able to induce polarization (electric). The phenomenon was later named as the magneto-electric effect. After few nice findings, rigorous research started on the magneto-electric effect to properly understand the effect. Although, the coupling between these two electrostatic fields was noticed earlier, however, it took a long time to experimentally observe the underlying phenomenon in Cr₂O₃. In light of the foreseen conclusion, that the freedom to induce polarization (magnetization) with externally applied magnetic (electric) field, might enable researchers to make useful practical devices, a lot of work was carried out that ranges from single phase materials to the composite materials [1].

In our research, we have focused on the tensorial magneto-electric (ME) effect. Keeping in view the importance of the magneto-electric effect in Physics and the correlation of the uniaxial anisotropic media with the fundamental optical effects, we have developed the theory in such a media, and have considered the propagation of the electromagnetic waves. By ignoring the higher order terms, we have transformed the Maxwell's equation under the linear magneto-electric effect. For the definition of our tensorial media, the permittivity tensor, the permeability tensor, and the magneto-electric tensor are considered as constant tensors. In addition, the anisotropic axes are introduced as an additional axes and the role of vectors is emphasized. The anisotropic magneto-electric coupling coefficient is defined as β’, and after the transformation of the Maxwell's equation it appears at the off diagonal place in the final result (matrix).

Due to the continuity, the parallel component of the wave vector remains unchanged, however, the perpendicular component of the wave vector changes. In order to find the dispersion relation for our case, we have imposed additional constraints on our final result, and have concluded that when an electromagnetic wave propagates through a tensorial uniaxial anisotropic magnetoelectric media it gives rise to the double Jones birefringence. The analytical solutions are plotted in Mathematica and for some special condition on the incident angle, it leads to the D'yakonov surface wave which decays with the magneto-electric parameter and travels on to the plane z=0. In addition, the surface wave proposed herein will be observable experimentally at an angle of 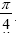. In developing the theory, we have also discussed the AC and DC dependence of frequency, where the developed theory principally works for all frequencies. The parameters such as 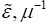, and the matrix notation of α normally used in experiments have been compared to the prior published findings of Hehl and coauthors, and in conclusion, the theory developed herein supports the Dzyaloshinskii's theory. The magneto-electric parameter is very significant from experiments and simulations point of view. It can be controlled and varied to study topological insulators, therefore, currently, this is our research direction.

References

1. Mahmood W, Zhao Q. The double Jones birefringence in magneto-electric medium. Sci Rep 5: 2015: 1-15.