Microwave Dielectric Properties of Water Saturated Carbonate Rocks

Abstract

The electromagnetic properties of forty water saturated limestone samples were measured at 9.54 GHz and reported. Measured average relative permittivity of the water saturated rocks was approximately (11.12, 0.0985). In addition to the dielectric measurements, the bulk density (ρT) and porosity (ΦT) were measured for all the 40 limestone samples. The porosity of the samples varies between 2% and 15%. The dielectric data (ε′ and ε″) were strongly correlated with ФT and ρT. The measured dielectric data were fitted with Bottcher, Looyenga, Maxwell, Bruggeman mixture formulae and TP model. There is a good correlation between the observed data and the data calculated from the models. The potential of using microwave tomography on limestone rock was examined based on the resulting properties.

Keywords

Limestone; Porosity; Bulk density; Electromagnetic characterization

Introduction

Rocks are multiphase systems consists of crystals as well as amorphous solids, liquids and gases. This confounds the investigation of physical properties, while the primary constituents of a stone are the strong minerals: properties, for example, the dielectric porousness and electrical conductivity are resolved primarily by the water substance, surface, and porosity. Their pores contain salt solutions of difference concentration and possibly gas and petroleum. The dielectric response of rocks whose pore is saturated with brine and oil is of great interest in oil exploration [1]. It is of great interest in applied physics to determine whether water- and –oil saturated rocks can be distinguished on the basis of ε′ values. More recent studies on a variety of materials such as calcite, dolomite and limestone are given in references [2-13]. There are few published data relating dielectric constant directly to porosity (Φ) for carbonate rocks [2,14]. Measurements of density and ε′ have been made on rocks and their corresponding powders by many researchers [15-17]. A considerable fraction of the volume of sedimentary rocks is composed of unoccupied space between the contacts of irregular grain boundaries i.e. pore space. When such rocks are fully saturated by a conducting fluid, such as brine, their conductivity will be related to porosity (Φ) empirically as, σ/σ_o=a Φ-m, where σ is the measured rock conductivity, σo is the conductivity of the saturating fluid [18]. a and m are empirical constants that vary with lithology of the rock formation. Quite often a is assumed to be unity and m found to vary a great deal in carbonates [6]. Focke and Munn have measured values ranging from 1.5 to 5.4 in carbonates from Middle Eastern reservoirs [19]. The pore structure in sedimentary rocks is however, very complex, and though a number of theoretical models for Archie’s law [20] and the corresponding porosity dependence of the permeability have been suggested [21]. Several studies have been reported in the literature on the dielectric properties of rocks but in most of them the reported experimental measurements had been made either at MHz or lower frequencies. The motivation behind this study is to explore the dielectric and electrical properties of sedimentary limestone tests regarding porosity, mass thickness, water immersion, and saltiness at microwave recurrence. This paper also provides statistical analyses relating ε′ and ε″ of a rock sample to its density, porosity and salinity of the saturating fluid (NaCl).

Experimental Methods

40 natural limestone samples were studied from Tamil Nadu state, India in this work. Samples each of three different thickn esses with the same cross sectional area have been cut from the same batch. The values of ε′ and ε″ at 9.54 GHz were determined using X-band Microwave Test Bench operated with Klystron oscillator and equipped with rectangular waveguide. Different components for X-band microwave bench were procured from M/S Vidyut Yantra Udyog, Modi nagar, India. The shortcircuited waveguide method for rectangular waveguide operating in TE10 mode at room temperature was employed. All the samples were shaped to a rectangular waveguide dimensions (2.2 cm × 1 cm). For accurate measurements of dielectric constant width at the twice minima method was used [22]. The sample was heated in a muffle furnace at 110°C for a period of 12 hours and then soaked in water for 24 hours. The sample was removed, the excess water was wiped off and its dielectric properties were determined.

Sample Porosity Measurements

The porosity of the limestone samples was determined using the procedure described in ASTM standard C20 (20). Three samples were prepared from a piece of each of the original rocks. Each specimen were weighed and then placed in deionized boiling water for a period of five hours. The process of boiling facilitated the displacement of trapped air and the saturation. After boiling, the samples were cooled at room temperature while still submersed. The samples were weighed while suspended in water and then removed and weighed in air. Finally, the samples were oven dried at a temperature of 90°C for approximately 12 hours, and 180°C for four additional hours and then weighed. The density and the porosity were calculated using the measurements described above. Sample density (ρ_T) were determined by the relation,

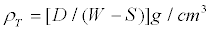      (1)

Where D is the oven dried weight, W is the weight of the saturated sample in air and S is the weight of the sample while submersed. The apparent porosity (Φ_T) was determined using the expression

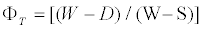      (2)

And the results obtained for 40 limestone samples have been reported in Table 1.

Table 1: Representative chemical compositions (wt. %) for samples in this study.

Measurement Accuracy and Precision

The measurement accuracy of the width at twice minima method was evaluated by comparing the dielectric constant measured by this method with the dielectric constant of standard materials. The reference materials are homogeneous, thick blocks of solid materials, such as fused silica and glass, whose dielectric constants had been accurately known. The dielectric constants of the silica and the glass were measured as 3.845 and 6.21 respectively. Agreement between our data and those of the literature value is quite good. Based on such comparisons, the wave guide measurement accuracy was found to be better than ± 0.04 of the measured values.

Results and Discussion

The representative chemical analysis report of the samples and the measured values of density (ρ_T), porosity (Ф_T), dielectric constants (ε′ and ε″), relaxation time (τ) and attenuation constant (α) for water saturated samples were presented in Tables 1 and 2. Each data point represents the average of four measurements corresponding to four orientations of samples within the waveguide. The variability among measurements made for a given rock sample is an indicator of the sample’s spatial inhomogeneity. Such variations may be due to density variations or to variations in chemical composition and crystalline structure among mineral constituents. In order to verify whether the absorbed water is distributed over the total volume of the specimens, we applied the same hydration procedure to three limestone specimens, having the same cross-sectional area, but different thickness, i.e. 3.98, 5.68, and 7.15 mm. It was found that the measure of water assimilated is relative to the volume of the examples, which demonstrates that water particles are appropriated through the main part of the materials.

Table 2: Measured values of bulk density (ρ_T), total porosity (Φ_T), dielectric constant (ε′), dielectric loss (ε"), attenuation (α) and relaxation time (T) for water saturated samples of carbonate rocks.

Dependence of Dielectric Permittivity on Water Saturation

The measured dielectric constant increased by about 1.44 times from ambient conditions (as received state, ARS). The loss more than doubled as the sample changed from ambient to saturated conditions. Figure 1 serves to illustrate the important of measuring Φ_T and ρ_T. Values of Φ_T plotted against ρ_T should produce a linear trend with y-axis intercept (T) of 1 and x-axis intercept (ρ_T) of ρ_s, the true density of the solid with no porosity. Different carbonate rock suites will have different x-axis intercepts because they have intrinsically different compositions and hence densities. The data forms a well-defined trend, but, because most samples have low porosity, it does not extrapolate precisely to a y-axis intercept (Φ_T) of 1 (corresponding to 100% air when the rock has no mass). The dielectric constant of wet rocks is a function of the dielectric constant of rock grains and the porosity. Comparison of dielectric constant with porosity indicates that dielectric constantly increases with the decrease of porosity (Figure 2a). This is to be expected because with lower porosity, the inter particle hindrance to dipolar motion increases giving rise to the higher values of ε′ and ε″ [4]. The dielectric constant of water is ≈ 80 and that of air is ≈ 1. Water in the pores is a chemical solution involving conductive mineral grains. Because these ions contribute to the apparent dielectric constant in an applied electric field, the dielectric constant of the solution in the pores is a little higher than ≈ 80.The dielectric constant of dried solid rock also is small compared to water. Therefore the apparent dielectric constant of rock strongly depends on the water saturation. This tendency is observed in the experimental results shown in Figure 2a. The data from all the suites form a smooth and definite pattern in ε′- Φ_T space of increasing dielectric constant with decreasing porosity. However further discussions concentrates only on the ALA-RC data. Various authors have proposed a variety of such mixing formulas for brine-saturated rocks and for other composite media. Five popular mixture formulae [23] were used in the present study for this study. The water is considered to be the conducting spherical particles uniformly dispersed in a limestone matrix. The resulting parameters show trends that should be close to those exhibited by the actual measurements. The permittivity of water used in the determination of the effective permittivity was (76.92, 6.64) for a temperature of 25°C. Both real and imaginary parts of the permittivity matched with the measured values quite well. From Figure 2b, the Looyenga formula has different trend, however, all the other four models have the same trend. In the present investigation, appreciable agreement between the theoretical values obtained by these methods and the experimentally observed values, it may be predicted that the rocks are having large cohesion in its particles and may serve as a continuous medium. These models fit with the data well and a plot of residuals shows a linear relationship with the porosity.

Figure 1: Values of Φ_T are plotted against ρT. Measured values have been fitted to model lines that extrapolate to values of solid density of 2.7 and 3.0 g /cm³.

Figure 2: Experimental data from this study are plotted as ε' vs. ΦT for all the suites. (b) Plot of ε' vs. ΦT compared to model fitted curves for ALA-RC data. (c) Plot of residuals on five fits to the ALA-DC data.

Microwave Conductivity and Formation Factor

The main interest in conductivity measurement is to determine the formation factor F as a function of porosity to test Archie’s law and the results are summarized in Figure 3. The porosity (Φ_T) ranges from 0.0186 to 0.1574. Po-Zen [24] established that for high porosity rocks correspond to m=1.5 and the low porosity correspond to m=2. i.e. m is higher for low porosity. In the present study, the value of m is calculated to be 1.78, which is in agreement with the Po-Zen [24] results Figure 4. There have been many attempts to understand this behavior, two simple models such as shrinking tube model and a grain consolidation model have been proved to be most illuminating. Archie’s law comes from the fact that the porosity and conductivity are influenced by different parts of a skewed pore size distribution. A large value of the exponent m implies that there are pores that contribute little to the conduction. There are two possible ways to characterize the low porosity data. First, it can be approximated by the solid line in Figure 5 which corresponds to a ≈ 1 and m ≈ 2 i.e., both a and m are constants over a large porosity. The low porosity data points correspond to m ≈ 2.26. Since the pore-space distribution changes continuously with Φ_T, it is perhaps more reasonable to think of m as also continuously varying with Φ_T, rather than being constant over a wide range of ΦT [24].

Figure 3: (a) Experimental data from this study are plotted as ε″ vs. ΦT for all the suites. (b) Plot of ε″ vs. ΦT compared to model fitted curves for ALA-RC data. (c) Plot of residuals on five fits to the ALA-DC data.

Figure 4: Experimental data from this study are plotted as (a) ε' vs. ρ_T (b) ε″ vs. ρ_T for all the suites.

Figure 5: Formation Factor of rock samples as obtained by conductivity measurements. The solid line is with a =1, m = 2, the dashed line corresponds to m = 2.26

Dependence of Relaxation Time on Porosity and Density of Wet Rocks

The values of relaxation time determined by the relation τ=ε″/ω ε′ are also reported in Table 1 for all the samples under investigation. The decrease in relaxation with water saturation is due to increasing hindrance to the process of polarization. The relaxation observed in fully saturated rocks at high frequencies may be caused by Maxwell-Wagner interlayer polarization, that is, by charge accumulation at the phase separation boundary [5]. Ions contained in pore solutions carry these charges. Figure 6 shows decrease in relaxation time with porosity and take the regression equation.

Figure 6: Values of are plotted against T.

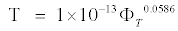      (3)

The decrease in relaxation time with increasing porosity can be caused by an increase in the amount of the saturating solution per unit volume of the sample, which increases the number of charge carriers. This speeds up the process of charge accumulation at pore boundaries. As a result, the value of dielectric constant due to Maxwell-Wagner effect increases.

Depth of Penetration

The depth of penetration into a material is governed by the propagation constant which in turn depends on the frequency of the electromagnetic energy and on the constitute parameters of the material. The propagation constant (γ) for a dielectric material is given by the expression Figure 7.

Figure 7: Values of α plotted against Φ_T.

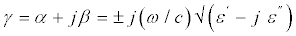      (4)

Where ω is the radiation frequency, ε′ and ε″ are the real and imaginary parts, respectively, of the complex permittivity of the material, α and β are attenuation and phase constants. The plus sign is used for the propagation in the positive direction. An expression for the attenuation constant in terms of the complex permittivity is found by expanding out the radical sign and taking the real part of the resulting expression. The attenuation constant is thus given by,

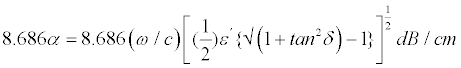      (5)

As the wave propagates in the material, the amplitude will decrease by the factor (e^-αz), where Z is the distance of the wave travels into the material. For a distance of (1/α), the wave will be attenuated by a factor of e^-1 or 0.368. The attenuation constant, therefore provides a measure of the practical depth of penetration into the material. The presence of absorbed water in the sample dramatically increases the dielectric loss component. As the above equation indicates, the attenuation is dominated by the imaginary term and thus, a corresponding increase in ε″ will result in an increase in the attenuation constant. For example, at 9.54 GHz, the complex permittivity for the saturated sample was measured to be ε*=(8.54, 0.26447) (sample code: ALA-1). These values lead to a calculated attenuation constant value of 0.2693 dB/cm. Therefore, in this case, as the loss term is increased by a factor of 4.8, there is a corresponding increase in the attenuation constant by a factor of 4.76. The penetration depth is likewise decreased from 6.07 to 1.274 cm, again by a factor of 4.76.

Influence of the Saturating Solution Salinity

The change in dielectric permittivity with salinity is defined by the porosity of the sample and the frequency of the electromagnetic field. When the rock porosity is low and the frequency of the electric field is high, then the dielectric permittivity is weakly dependent on the salinity [5]. Figure 8 illustrates the relationship of dielectric permittivity measured at 9.54 GHz to the porosity of carbonate rocks with C=300 g/L and C=150 g/L. The increase of dielectric permittivity ε′ with porosity for samples with C=150 g/L is more abrupt than with C=300 g/L and can be described by the following linear equation,

Figure 8: Dielectric constant versus porosity (%) for rock samples with various salinity solutions.

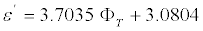      (6)

For samples with C=300 g/L the regression equation takes the form,

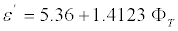      (7)

Figure 8 shows that ε' increases linearly with an increase in salinity. It corresponds to the change in the conductivity of NaCl solution with concentration. For higher concentrations of solution, the dependence of ε' on concentration is weakened, as shown by the changing slope of the curves. At high porosities, ε' increases more sharply (Figure 9). With an increase in salinity for a given porosity or an increase in porosity for a given salinity, there is an increase in the number of charges per unit volume, which causes an increase in dielectric constant ε'. Figure 10 shows the nonlinear decrease τ with concentration of solution for limestone samples of various porosity. The decrease in τ with an increase in salinity of the saturating solution can be attributed to an increase in the rate of change accumulation on pore boundaries due to better solution conductivity. Samples with high porosity usually have smaller τ values, which decline more sharply. It was found that [1,7] the parameters of relaxation process in the high frequencies are determined by the sample porosity and the salinity of the saturating solution and depend less on lithologic type. As shown in Figures 10 and 11 for various limestone samples, the relaxation time decreases hyperbolically with time. The correlation for all limestone samples with C=300 g/L can be described by the regression equation

Figure 9: Dielectric constant versus salinity solution for rock samples with various porosities.

Figure 10: Relaxation time versus salinity of solution for rock samples with various porosities.

Figure 11: Relaxation time versus porosity (%) for rock samples with various salinities of the solution.

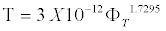      (8)

For samples with C=150 g/L, the τ=F (Φ_T) is higher and can be described by the regression equation

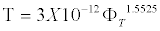      (9)

Conclusion

The results of the study suggest that the heterogeneity influences significantly the permittivity. Going from dry to highly hydrated samples, the absorbed water molecules lead to an enhancement of the complex permittivity ε*, and after the conductive mechanism of the rock matrix. The mixing theory was used to predict the change in the permittivity as a function of volume percent absorbed water. The predicted dielectric constant (ε′ and ε″) values were very close to the actual measured values. The depth of penetration into the water-saturated samples was calculated.

References

1. Levitskaya TM and Sternberg BK. Polarization process in rocks 2. Complex dielectric permittivity method. Radio Sci. 1996;31:781-802.
2. Kenyon WE. Texture effects on megahertz dielectric properties of calcite rock samples. J. Appl.Phys. 1984;55:3153-3162.
3. Ulaby FT, et al. Microwave dielectric properties of dry rocks. IEEE Trans. Geosci.RemoteSensing. 1990;28:325-336.
4. LesmesDP and Morgan FD. Dielectric spectroscopy of sedimentary rocks. J. Geophys.Res.106 (B7). 2001:13329-13346.
5. Levitskaya TM and Sternberg BK. Polarization process in rocks 1. Complex dielectric permittivity method. Radio Sci.1996;31:755-779.
6. Sen PN. et al. Formation factor of carbonate rocks with microporosity: model calculations. J. Petro.Sci.Engg. 1997;17:345-352.
7. Levitskaya TM andNosava YE. Dependence of dielectric permittivity in dolomites upon mineralization of a saturating solution. Earth Phys. 1986;22:512-514.
8. Nelson SO. Coal and limestone by measurements on pulverized samples. J. Microwave power and Electromagnetic energy. 1996;31:215-220.
9. Garrouch A, et al. The influence of clay content, salinity, stress, and wettability of the dielectric properties of brine-saturated rocks: 10Hz-10MHz. Geophysics. 1994;59:909-917.
10. Sharma MM, et al. Effects of wettability, Pore Geometry, and Stress on Electrical conduction in Fluid-Saturated Rocks. The Log Analyst. 1991;32:511-525.
11. Frasch LL, et al. Electromagnetic properties of dry and water saturated basalt rock, 1-110GHz. IEEE Trans.Geosci. Remote Sensing. 1998;36:754-765.
12. Taherian MR, et al. Measurement of dielectric response of water-saturated rocks. Geophysics. 1990;55;1530-1541.
13. Sen LC, et al. Dielectric properties of reservoir rocks at ultra-high frequencies. Geophysics. 1985;50:692-704.
14. CambpellMJ andUlrichs J. Electrical properties of rocks and their significance for lunar radar observations. J. Geophys. Res. 1969;25:5867-5881.
15. Frisnillo AL, et al. Effects of vertical stress, temperature and density on the dielectric properties of lunar samples 72441,12,15301,38 and terrestrial basalt. Earth Planet. Sci. Lett. 1975;24:345-356.
16. Frasch LL. Electromagnetic properties of Dry and Water Saturated BasaltRock, 1-110 GHz. IEEE Trans. Geosci. Remote sensing. 1998;30:754-766.
17. ArchieGE. The electrical resistivity log as an aid indetermining somereservoir characteristics. Trans. AIME. 1942;146:54-67.
18. Focke JW and Munn D. Cementation components (m) in Middle Eastern Carbonate reservoirs presented at Middle Eastern oil show.Bhahrain, Soc.Pet. Eng, Pap. 1985;SPE 13735:431-442.
19. NigmatullinRR,et al. A fractal pore model for Archie’s law in sedimentary rocks. J. Phys. D:Appl. Phys. 1991;25:32-37.
20. ArchieGE. The electrical resistivity log as an aid indetermining somereservoir characteristics. Trans. AIME. 1942;146:54-67.
21. Lance AL. Introduction to Microwave Theory and Measurements, MC Graw Hill Co, New York.1964.
22. Maxwell–Ganett JC. Colours in metal glasses and in metal films. Trans R. Soc. Lond. 1904;203:385-420.
23. Wong, et al. Conductivity and Permeability of rocks.Phys. Rev. 1984;30:6606 -6614.
24. Frisnillo AL, et al. Effects of vertical stress, temperature and density on the dielectric properties of lunar samples 72441,12,15301,38 and terrestrial basalt. Earth Planet. Sci. Lett. 1975;24:345-356.