Neutronic Calculations of Ghana Research Reactor-1 LEU Core

Abstract

Presenting neutronic calculations relating to the Ghana Research Reactor-1 (GHARR-1) LEU core is the goal of this article. These are key factors for maintaining safe and reliable core operations of the reactor. The neutronic parameters are: multiplication factor (keff), clean cold core excess reactivity (ρex), control rod worth (CRW), neutron flux distribution in the inner and outer experimental channel and the delayed neutron fraction. A Monte Carlo-N-Particle (MCNP5) neutronic simulation code was employed in this study. These calculations were done before the final core loading and the subsequent experimental Zero Power Test (ZPT) of the GHARR-1. The excess reactivity of the LEU core was calculated to be 4.03 ± 0.05 mk. This study indicates that, the reactor is operated under safe and reliable condition.

Keywords

Low enriched uranium, Miniature neutron source reactor

Introduction

Ghana Research Reactor-1 is a miniature neutron source reactor (MNSR), developed by the Chinese Institute of Atomic Energy (CIAE). The reactor is a compact research reactor designed to mimic the Canadian SLOWPOKE reactor design Figure 1. The MNSR is favored all over the world because of its inherent safety [1]. The reactor has simple auxiliary facilities, reliable cooling systems and shielding. The MNSR which is a 34 kW power tank-in-pool type of research reactor that uses low enriched uranium (13.0% U-235) as fuel, beryllium as reflector and light water as coolant, moderator and as a biological shielding. Primarily, the MNSR is used for teaching and learning and the neutron source for research activities such as neutron activation analysis (NAA) [2,3]. The reactor core consist of the fuel cage, the control rod guide tube which houses the only control rod, fuel rods, dummy rods and tie rods. Heat generated during reactor operation is removed by natural convection. The MNSR has five inner experimental channels, four reactivity regulators and two fission chambers which are located inside the annulus beryllium reflector while five outer experimental channels are located outside, as shown in Figure 2.

Figure 1: Vertical cross-section view of GHARR-1 MNSR

Figure 2: Horizontal cross-section view of GHARR-1 MNSR

Technical summary of the reactor is presented in Table 1.

Table 1. Technical summary of GHARR-1 MNSR [CIAE].

Maximum thermal neutron flux is obtained in the inner experimental sites that correspond to clean cold excess reactivity of approximately 4 mk (mk=10^-3 (Δk/k)). To compensate a long-term reactivity of the reactor, one or more beryllium shim is added to the top shim tray. A Monte Carlo-N-Particle (MCNP5) code was employed to simulate the excess reactivity (ρ_ex), shutdown margin (SDM), average flux distribution in the inner and outer experimental sites, control rod worth (CRW) and delayed neutron fraction.

Methodology

A 3-D Monte Carlo transport code of GHARR-1 LEU-core reactor was modified to reflect the changes in the equipment. Nuclear data for fissile and non-fissile isotopes associated with components of the physical model were selected from a number of evaluated data libraries; ENDF/B-VI, ACTL, ACTI, etc. A special scattering, S(α,β) was applied specifically to treat thermal scattering in the metallic beryllium reflector and in light water for water regions of GHARR-1 [4]. Neutronic analysis were performed using condensed three-group energy structure; 0 – 0.55 eV, 0.55 eV – 0.1 MeV and 0.1 MeV – 20 MeV for thermal, epithermal and fast neutrons respectively. The computations were performed using 600000 source neutrons per cycle for a total of 530 k_eff cycles and an initial k_eff guess of 1.004 was chosen for which 30 k_eff cycles were skipped to allow source neutrons to adjust to equilibrium before final k_eff was estimated. The criticality source card with initial criticality was used to estimate the k_eff and its corresponding excess reactivity ρ_ex with all the fuel elements as fission source points. TOTNU NO card was also used to estimate the criticality for average prompt neutrons for all the fissionable nuclides. The model also provided for the simulation of average neutron flux distribution in the inner and outer irradiation sites by evoking the F4 tally which calculates the flux distribution using the track length within the specified energy ranges in a unit volume [5]. The out-put data were then normalized using the expression in equation 1.

Theory

Normalization Expression

The un-normalized out-put obtained after the MCNP simulation was normalized to get the actual neutron fluxes. This is accomplished by utilizing some parameters like loss to fission ratio, neutron fission q-value provided in the MCNP code.

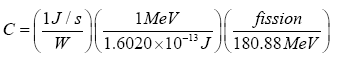(1)

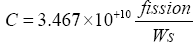
Then the normalization factor for the un-normalized tallies obtained from the MCNP simulation was calculated by the expression below [3];

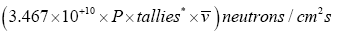(2)

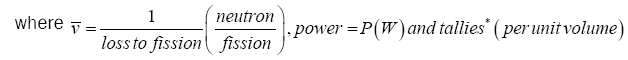
Delayed Neutron Fraction

In Monte Carlo calculations, consider the introduction of a neutron with properties 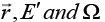in a critical reactor system with zero power. This neutron will induce fission thereby producing other neutrons and these neutrons will in turn cause another fission which lead to further neutrons production. The number of fission produced in this way will approach a limit, which is given by the iterated fission probability which is proportional to the adjoint function.

Using the prompt method,

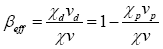(3)

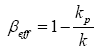(4)

Where k and k_p are the eigen-values for all neutrons and only prompt neutrons respectively.

Shutdown Margin

The shutdown margin characterizes the core multiplication capabilities in the shutdown state and also relates to the rate at which the power level may be reduced in an emergency shutdown. Shutdown margin ρ_sm can be obtained from the relation [6].

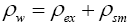(5)

where ρ_w, control rod worth, ρ_ex the excess reactivity and ρsm the shutdown margin, k_in and k_out being the eigenvalues for total rod insertion and withdrawal respectively. Hence,

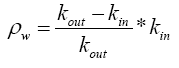(6)

which gives,

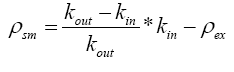(7)

Results and Discussion

The result obtained for the nuclear criticality, core excess reactivity and the control rod worth of the LEU are presented in Table 1. The table shows some eigenvalues with its associated errors for GHARR-1 LEU core when the control rod is fully withdrawn from the core and when it is fully inserted into the core. The worth of the control rod was found to be 7.13 mk which is close to the value reported by other authors. The core excess reactivity was calculated to be 4.03 mk.

The TOTNU NO card was used with the control rod withdrawn to estimate the effective delayed neutron fraction as presented in Table 2.

Table 2. Calculated neutronic parameters for GHARR-1 LEU core.

Shutdown margin of 3.09 mk was obtained for the control rod of the LEU core. Again, the average neutron flux distribution in the inner and the outer irradiation sites of GHARR-1 LEU core is similar to those reported by other authors (Figures 3 and 4).

Figure 3: Average Neutron flux distribution in inner irradiation channels.

Figure 4: Average neutron flux distribution in outer irradiation channels.

Conclusion

In this work, neutronic calculations have been performed for the Ghana Research Reactor-1 LEU core using MCNP5 simulation code. The results showed that the criticality calculations of the LEU are in good agreement with the HEU.

References

1. Zhou Y. IAEA-TECDOC-384, Technology and use of low power research reactors, Report of IAEA Consultants Meeting, Beijing, China. 1986;89-98.
2. Odoi H, et al. Conversion of International MNSR-Reference Case of Ghana MNSR. In 34th International Meeting on Reduced Enrichment For Research and Test Reactors 2012;2-5.
3. Birikorang SA, et al. Feasibility study of photo-neutron flux in various irradiation channels of Ghana MNSR using a Monte Carlo code. Annals of Nuclear Energy 2011;38:1593-1597.
4. Rose PF. ENDF-201, ENDF/B-VI Summary Documentation, BNL-NCS-17(Brookhaven National Laboratory) 1991.
5. Brewer R. Criticality Calculations with MCNP: A Primer. Retrieved from http://www.osti.gov/energycitations/product.biblio.jsp?osti_id=10171566
6. Ibrahim YV, et al. Annals of Nuclear Energy Monte Carlo simulation of additional safety control rod for commercial MNSR to enhance safety. Annals of Nuclear Energy 2012;44:71-75.