On the Disservice of Theoretical Physics (Work on the Bugs)

Abstract

One should not think that the fundamental scientific knowledge can be harmful. Most of theoretical physicists adequately reflects the physical reality and forms the basis of our knowledge of nature. However, some physical theories arised in the twentieth century are not supported by experimental data. At the same time impression of their credibility masked by a very complex mathematical apparatus is so great that some of them are even awarded the Nobel Prize. However, the fact it does not change a number of generally accepted theories created in the twentieth century are not supported by the experience and therefore should be recognized as pseudoscientific and harmful.

Keywords

Physics of star, Terrestrial magnetism, Superconductivity, Superfluidity, Thermo-magnetic effect, Neutron, Deuteron.

Introduction

The twentieth century ended and removed with every year further and further from us. Already possible to summarize its scientific results. The past century has brought great discoveries in the field of physics. At the beginning of the XX century was born and then rapidly developing nuclear physics. It was probably the greatest discovery. It radically changed the whole material and moral character of the world civilization. In the early twentieth century, the radio was born, it gradually led to the television, and radiotechnics gave birth to computers. Their appearance can be compared with the revolution that occurred when people have mastered fire. The development of quanta physics led to the emergence of quantum devices, including the lasers shine. There is a long list of physical knowledge, which gave us the twentieth century.

Experimentalists and Theoreticians

The important point is that the twentieth century has led to the division of physicists on experimentalists and theorists. It was a natural process caused by the increasing complexity of scientific instruments and mathematical methods for constructing theoretical models. The need for the use of the vacuum technics, the low-temperature devices, the radio-electronic amplifiers and other subtle techniques in experimental facilities has led to the fact that the experimenters could be the only people who can work not only with your head but can do something their own hands. On the contrary, people are more inclined to work with the mathematical formalism could hope for success in the construction of theoretical models. This led to the formation of two castes or even two breeds of people. In only very rare cases physicists could be successful on the both experimental and theoretical “kitchen”. The most striking scientist of this type was Enrico Fermi. He was considered as their own in the both experimental and theoretical communities. He made an enormous contribution to the development of quantum and statistical mechanics, nuclear physics, elementary particle physics, and at the same time created the world’s first nuclear reactor, opening the way for the use of nuclear energy. However, in most cases experimentalists and theorists is very jealous of each other. There are many legends about what theorist is sad sack. So there was a legend about the Nobel Prize winner - theorist Wolfgang Pauli, according to which there was even a special “Pauli effect”, which destroyed the experimental setup only at his approach. One of the most striking instances of this effect, according to legend, took place in the laboratory of Frank in Gottingen. Where a highly complex experimental apparatus for the study of atomic phenomena was destroid in a completely inexplicable reason. Frank wrote about the in cident Pauli in Zurich. In response, he received a letter with a Danish mark, in which Pauli wrote that he depart to see on the Niels Bohr, and during a mysterious accident in the J. Frank laboratory he was in the train which just made a stop in Gottingen. At the same time, of course, theorists began to set the tone in physics, because they claimed they can understand all physics wholly and to explain all of its special cases. Outstanding Soviet theorist of the first half of the twentieth century was Ya. Frenkel. He wrote a lot of very good books on various areas of physics. Even some anecdote went about his ability to explain everything. Supposedly once some experimenter caught his at a corridor and showed some experimentally obtained curve. After a moment of thinking, Ja.Frenkel gave an explanation of the curve course. That it was noted that the curve was accidentally turned upside down. After this rotating it in place and a little reflection, Ja. Frenkel was able to explain this dependence too.

On the Specifics of the Experimental and the Theoretical Working

The features of relations of theoreticians and experimentalists to their work are clearly visible on the results of their researches. These results are summarized for illustrative purposes in Table 1. The situation with experimental studies is simple. At these studies, various parameters of samples or the properties of the physical processes are measured. If such measurements are not supplemented by a theoretical description of the mechanisms that lead to these results, this study can be regarded as a purely experimental. It can be placing in the box 1 in the table. If an experimental study is complemented by a description of the theoretical mechanism that explains the experimental data, it’s just good physical research. Put such work in the box 2. Also the different situation is possible when the theoretical study of the physical effect or object is brought to the “numbers” which is compared with the measured data. That is essentially to think, that these studies are of the same type as the studies in box 2. However, as there is an emphasis on the theory of physical phenomena, these studies can be placed in the box 3. As a result of this classification, the theoretical studies which have not been confirmed experimentally must be placed in box 4.1. If the theoretical studies are not brought to the numerical results, which can be tested experimentally, they are placed in this box too. Surprisingly, there are quite a few of these theoretical compositions. For example, the description of the super-phenomena-superconductivity and superfluidity (eg [2] - [4]) - abounds with complex derivation of formulas giving the generalized characteristics and general properties of superconductors, but their descriptions are never reaches the “number” which is characterizing the properties of separate superconductor. Despite the obvious speculative nature of such theories, some of them received full recognition in the physics community.

Naturally, the question arises how bad the theoretical approach which is used to describe these phenomena, because it violates the central tenet of natural science (Table 1)

Table 1: The Systematics of Physics Research

The Central Principle of Science

The central principle of natural science was formulated more than 400 years ago by William Gilbert (1544-1603). One might think that this idea, as they say, was in the air among the educated people of the time. But formulation of this postulate has come down to us due to Gilbert’s book [1]. It formulated simply: “All theoretical ideas claiming to be scientific must be verified and confirmed experimentally”. Until that time false scientific statements weren’t afraid of an empirical testing. A flight of fancy was incomparably more refined than an ordinary and coarse material world. The exact correspondence of a philosophical theory to a experiment was not necessary. That almost discredited the theory in the experts’ opinion. The discrepancy of a theory and observations was not confusing at that time. In the course there were absolutely fantastic ideas from our point of view. So Gilbert [1] writes that he experimentally refuted the popular idea that the force of the magnet can be increased, rubbed with garlic. Moreover one of the most popular questions at the religious and philosophical debates had the quantitative formulation: how many angels can stay on the tip of the needle?

Galileo Galilei (1564-1642) lived a little later Gilbert [1] had develop this doctrine and formulated three phase of testing of theoretical propositions:

(1) To postulate a hypothesis about the nature of the phenomenon, which is free from logical contradictions;

(2) On the base of this postulate, using the standard mathematical procedures, to conclude laws of the phenomenon;

(3) By means of empirical method to ensure, that the nature obeys these laws (or not) in reality, and to confirm (or not) the basic hypothesis.

The use of this method gives a possibility to reject false postulates and theories.

The Characteristic Properties of Pseudo-theories of XX Century

In the twentieth century, there were several theories that do not satisfy to the general postulate of science.

Many of them simply are not brought to ensure that their results could be compared with the measurement data of the objects [2]. Therefore it is impossible to assess their scientific significance. These pseudo-theories use always complicated mathematical apparatus, which tends to replaces them the required experimental confirmation. Simplistically the chain of reasoning, which can be formed, for example, by a student at his acquaintance with these theories may be as the next sequence:

• Theory created by the author is very complex;

• This means that the author is very smart and knows a lot;

• So smart and well-trained theorist should not be mistaken;

• It means his theory is correct.

All links in this chain of reasoning may be correct. Except the last. Theory is valid only if it is confirmed by experiments. It is essential that pseudo-theories cannot be simplified for obtaining of an approximate, but correct and simple physical constructions. The correct approach to the explanation of the object can be mathematically difficult, if it aimed on an accurate description of the properties of the object. This approach should allow getting a simple estimation on the order of value. Another feature of pseudo-theories consists in substitution of experimental proofs [3]. All objects under consideration of physical theories have main individual properties that can be called paramount. For stellar physics they are individual for each star radius, temperatures, and masses. For superconductors - individual for each critical temperatures and magnetic fields, for superfluid helium - the transition temperature and the density of atoms near it, and so on. Quasi-theories are not able to predict the individual paramount properties of considered objects. They replace the study of the physical mechanisms of the formation of these primary parameters on a describing of general characteristics of the physics of the phenomenon and some of its common properties. For example, the theory of XX-th century substituted the explanation of the properties of specific superconductors by the prediction of the observed temperature dependence of the critical field or the energy gap which are characteristic for this phenomenon. As a result, it appears that there is an agreement between theory and experiment, although the general characteristics of the phenomenon can usually be called thermodynamic. Let consider some specific pseudo-theory by theoretical physics in the twentieth century [4].

The Theory of the Internal Structure of Hot Stars

Some theoretical constructs could be built only speculatively, since desired experimental data was not existed.

Astrophysicists in the twentieth century were forced to create a theory of the internal structure of stars, using a special method. The foundation of the theory of the internal structure of stars in the twentieth century was not the observational data, which at the beginning of the century it was not simple. Instead of the measurement data, the general amount of astrophysical knowledge and models of stars was used as base of this theory. The self-consistency of this information gave the impression of an objective correctness of this theory.

Eddington, et al. They formulated first the basic ideas of the theory of stars. Conservatism of this approach lies in the fact that some very important scientific achievements remain “over- board” if they were obtained by physical science after the formulation of the canons. This happened with the laws of physics of hot dense plasma, which were formulated much later, than foundations of astrophysics. They were not included in its base. This is crucial because this plasma forms stars.

The modern astrophysics continues to use a speculative approach. It elaborates qualitative theories of stars that are not pursued to such quantitative estimates, which could be compared with the data of astronomers [5,6]. The technical progress of astronomical measurements in the last decade has revealed the existence of different relationships that associate together the physical parameters of the stars. To date, these dependencies are already accumulated about a dozen. The temperature-radiusmass- luminosity relation for close binary stars, the spectra of seismic oscillations of the Sun, distribution of stars on their masses, magnetic fields of stars (and etc.) have been detected. All these relationships are de- fined by phenomena occurring inside stars. Therefore, a theory of the internal structure of stars should be based on these quantitative data as on boundary conditions. Of course, the astrophysical community knows about the existence of dependencies of stellar parameters which was measured by astronomers. However, in modern astrophysics it is accepted to think, that if an explanation of a dependency is not found, that it can be referred to the category of empirical one and it need no explanation. It seems obvious that the main task of modern astrophysics is the construction of a theory that can explain the regularity of parameters of the Sun and stars which was detected by astronomers. The reason that prevents to explain these relationships is due to the wrong choice of the basic postulates of modern astrophysics. Despite of the fact that all modern astrophysics believe that the stars consist from plasma, it historically turned out that the theory of stellar interiors does not take into account the electric polarization of the plasma, which must occur within stars under the influence of their gravitational field. Modern astrophysics believes that the gravity-induced electric polarization (GIEP) of stellar plasma is small and it should not be taken into account in the calculations, as this polarization was not taken into account in the calculations at an early stage of development of astrophysics, when about a plasma structure of stars was not known. However, plasma is an electrically polarized substance, and an exclusion of the GIEP effect from the calculation is unwarranted. Moreover without of the taking into account of the GIEP-effect, the equilibrium stellar matter cannot be correctly founded and a theory would not be able to explain the astronomical measurements. Accounting GIEP gives the theoretical explanation for the all observed dependence [7]. So the figures show the comparison of the measured dependencies of the stellar radius and the surface temperature from the mass of stars (expressed in solar units) with the results of model calculations, which takes into account the effect GIEP (Figures 1 and 2).

Figure 1: Theoretical dependence of the surface temperature on the mass of the star in comparison with the measurement data. The theory takes into account the presence of the gravity induced electric polarization of stellar plasma. Temperatures are normalized to the surface temperature of the Sun (5875 K), the mass - to the mass of the Sun.

Figure 2: Theoretical dependence of the radius of the star on its mass in comparison with the measurement data. The theory takes into account the presence of the gravity induced electric polarization of stellar plasma. Radius expressed in units of the solar radius, mass - in units of mass of the Sun.

The calculations with accounting of the GIEP-effect are able to explain the observed spectrum of seismic solar oscillations (Figure 3) and measurements of the magnetic moments of all objects in the solar system, as well as a number of stars (Figure 4). In general, the accounting of GIEP effects gives the explanation to all the data of astronomical measurements by building the star theory, in which the radius, mass, and temperature are expressed by the corresponding ratios of the fundamental constants, and individuality of stars are determined by two parameters - by the charge and mass numbers of nuclei, from which a stellar plasma is composed. The important feature of this stellar theory, which is built with the GIEP accounting, is the lack of a collapse in the final stage of the star development, as well as “black holes” that could be results from a collapse. Only by relying on measurement data, physics of stars can get rid of speculations and obtain a solid foundation on which must be built any physical science [8].

Figure 3: (a) The measured power spectrum of solar oscillation. The data were obtained from the SOHO/GOLF measurement [8]. (b) The theoretical spectrum calculated with taking into account the existence of electric polarization induced by gravity in the plasma of the Sun [7].

Figure 4: The observed magnetic moments of cosmic bodies vs. their angular momenta. On the ordinate: the logarithm of the magnetic moment over Gs • cm³. On the abscissa: the logarithm of the angular momentum over erg • s. The solid line is according to Blackett’s dependence.

The Theory of Terrestrial Magnetic Field

The modern theory of terrestrial magnetism try to explain why the main magnetic field of the Earth nears the poles is of the order 1 Oe. According to the existing theoretical solution of this problem, there is a special mechanism of hydro-dynamo which generates electric currents in the region of the Earth’s core [9]. This model was developed in the 1940’s -1950’s. At present it is generally adopted. Its main task - to give an answer: why the main magnetic field of the Earth near the poles is of the order of 1 Oe? Such statement of the basic problem of terrestrial magnetism models nowadays is unacceptable. Space flights, started in 1960’s, and the further development of astronomy have allowed scientists to obtain data on magnetic fields of all planets of Solar system, as well as some their satellites and a number of stars. As a result, a remarkable and earlier unknown fact has been discovered. It appears that the magnetic moments of all space bodies (those which have been measured) are proportional to their angular momenta. The proportionality coefficient is approximately equal to G^1/2/c, where G is the gravitational constant; c is the velocity of light (4). Amazing is that this dependence remains linear within 20 orders of magnitude! This fact makes it necessary to reformulate the main task of the model of terrestrial magnetism. It should explain, first, why the magnetic moment of the Earth, as well as of other space bodies, is proportional to its angular momentum and, second, why the proportionality coefficient is close to the above given ratio of world constants. As the pressure in the Earth’s core is large enough to break the outer electron shells of atomic substances, this core should consist of electron ion plasma. The action of gravity on such a plasma lead to its electric polarization into the Earth core. The rotation of electrically polarized core (along with the entire planet) induces the terrestrial magnetic moment. The magnetic moment and the moment of the rotation of Earth can be calculated in the framework of the model of the Earth at a minimizing its total energy the results of these calculations are in good agreement with measured data [10]. This mechanism, which is a consequence of the law of universal gravitation, is workable in the case of all other (large) celestial bodies.

Superconductivity and Superfluidity

Superfluidity and superconductivity, which can be regarded as the superfluidity of the electron gas, are related phenomena. The main feature of these phenomena can be imagined, if to assume that into superconductors as well as into superfluid helium a special condensate is formed from particles which are interconnected by attraction energy. This mutual attraction does not allow a scattering of individual particles on defects and walls, if the energy of this scattering is less than the energy of the attraction. Due to the lack of scattering condensate acquires the ability to move without a friction. Superconductivity was discovered over the century ago, and the superfluidity of about thirty years later. However, despite the attention of many scientists to the study of these phenomena, they was long been the most mysterious in condensed matter physics. This mystery was attracting for the best minds of the last century. About it V.Ginzburg said directly in his Nobel speech. The mystery of the superconductivity phenomenon has begun to drop in the middle of the last century when the effect of magnetic flux quantization in superconducting cylinders was studied. This phenomenon was predicted even before the war by brothers London and London, but its measurements were made only after two decades. At about the same time it was observed that the substitution of one isotope of the superconducting element to another leads to a changing of the critical temperature of superconductors - the so-called isotope effect. This effect was interpreted as a proof of the main role of phonons in the formation of the superconducting state. Phonon mechanism was the basis of the Bardeen-Cooper-Schrieffer theory (BCS), which gets universal recognition, and in fact is generally accepted theory of superconductivity up to now.

However at this, the link between superconductivity and superfluidity was as if to disrupted there are no phonons into liquid helium for a combining of atoms. Coincidence of two regularities the changing of critical temperature at the isotope effect and the upper boundary of the phonon spectra of crystals - is not evidence of the role of phonons in the mechanism of the onset of superconductivity. To proof of the role of phonons must be shown that the result of the calculation of the phonon mechanism of superconductors is in accord with the measurement data. It seems natural to consider that the main property of the superconductor is its critical temperature (and the critical field). Therefore the proof of the reliability of a theory should be in the correct description of the critical parameters of superconductors. But it is failure: the theory based on the electron-phonon interaction, cannot calculate the critical temperature of the superconductor. More precisely in the BCS-theory, the expression for the critical temperature of superconductor obtains an exponential form the exponent of which contains the intractable in measurement factors, and this formula has no a practical interest. So the BCS theory does not give any clear predictions of the critical parameters of superconductors and there is nothing to compare with experiment. This can be seen as a consequence of the fact that the BCS-theory is focused on the mechanism of association of electrons in the bosonic pairs. But this association is not sufficient for the occurrence of superconductivity. The association to pairs is only a necessary condition. Couples born unifying mechanism are not identical. They differ in phase and polarization of uncorrelated zero-point oscillations. For the appearance of the superconducting state, these zero point oscillations must be ordered by means of additional forces of mutual attraction. On the other hand, the BCS theory can be attributed to complex mathematical theories. Only the presentation of its mathematical apparatus requires several lectures. At this it’s important feature is that it cannot be simplified so that its mechanism could be give approximations and estimates. It seems that the opportunity to do the calculations of the investigated phenomenon with varying degrees of complexity and accuracy should be a key feature for any workable theory of physical phenomena. Ya. Frenkel can be considered as the largest pre-war Soviet physicist. He often argued that mathematics is only a technology in the kitchen theorists. He was speaking that often modern theorists were losing a physical meaning of phenomena through overabundance of formulas. It can be attributed to the BCS-theory as this theory defies simplification. Besides seems unacceptable that the BCS-theory breaks the obvious connection between superconductivity and superfluidity in liquid helium no phonons combining atoms. More than fifty years of a study of the BCS has shown that this theory successfully describes the general features of the phenomenon, but it cannot be developed in the theory of superconductors. It explains general laws as the emergence of the energy gap, the behavior of specific heat capacity, the flux quantization, etc., but it cannot predict the main parameters of the individual superconductors their critical temperatures and critical magnetic fields. Something similar happened with the description of superfluidity. Soon after its opening, LD Landau in his first papers immediately showed that this phenomenon should be considered as a result of formation of a condensate, which consists of a macroscopic number of atoms in the same quantum state and obeys quantum laws. It gives the possibility to describe the main features of this phenomenon - the temperature dependence of the superfluid phase density, the speed of sound, etc. but it does not give an answer to the question of which physical mechanism leads to the unification of the atoms in the superfluid condensate and what is the critical temperature of the condensate. On the whole the description of both super-phenomena-superconductivity and superfluidity in their condition to the beginning of the XXI century induced a some feeling of dissatisfaction primarily due to the fact that there was not assumed a common mechanism of their occurrence. With regard to the proposition which was accepted in the last century that the phonon mechanism is the only possible mechanism of superconductivity, more recent experiments have shown that this proposition is incorrect. Experiments have shown that the zero-point oscillations of ions into lattices of superconducting metals are harmonic. As a result, the replacement of one isotope to another leads to a change in the amplitude of these oscillations, i.e. there is a influence of isotope mass on the interatomic distances in a metal lattice. As a consequence, the change of the isotope has a direct impact on the Fermi energy of a metal, i.e. directly on its electronic system, and phonons do not play any role in this effect. At very low temperatures, in which there is superfluidity in helium and superconductivity in metals all movements of particles are freezed except their zero-point oscillations. Therefore, as an alternative, we should consider the interaction of super-particles through electromagnetic fields of zero-point oscillations. This approach proves fruitful. At the consideration of super-phenomena as consequences of the zero-point oscillations ordering, one can construct theoretical mechanisms enabling to give estimations for the critical parameters of these phenomena which are in satisfactory agreement with measurements [10]. In a result, one can see that the critical temperatures of superconductors as I-type, well as II-type are equal to about 10⁻⁶ from the Fermi temperature superconducting metal, which is consistent with data of measurements (Figure 5).

Figure 5: The comparison of the calculated values of critical temperatures of superconductors with measurement data. Circles relate to type-I superconductors, squares show type-II superconductors. On the abscissa, the measured values of critical temperatures are plotted, on ordinate, the calculated estimations are plotted.

At this the destruction of superconductivity by application of critical magnetic field occurs when the field destroys the coherence of zero-point oscillations of electron pairs. This is in good agreement with measurements also (Figure 6).

Figure 6: The comparison of the calculated energy of superconducting pairs in the critical magnetic field with the value of the superconducting gap. Here, the following key applies: filled triangles - type-II superconductors, empty triangles – type - I superconductors. On vertical axis - logarithm of the product of the calculated value of the oscillating dipole moment of an electron pair on the critical magnetic field is plotted. On horizontal axis - the value of the gap is shown.

A suchlike mechanism works in superfluid liquid helium. The problem of the interaction of zero-point oscillations of the electron shells of neutral atoms in the s-state was considered yet before the war by London. He has shown that this interaction is responsible for the liquefaction of helium. The closer analysis of interactions of zero-point oscillations of helium atoms shells shows that at first at the temperature of about 4K only one of the oscillation modes becomes ordered. As a result, attraction forces appear between atoms which are need for helium liquefaction. To create a single quantum ensemble it is necessary to reach the complete ordering of atom oscillations. The calculation shows that the temperature of complete ordering of zero-point oscillations depends on the universal constants only [10]:

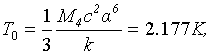(1)

Where M4 is mass helium atom, α is the fine structure constant. This value is a very good agreement with the measured value of the superfluid transition temperature T_λ = 2:172K.

Also in this case it is possible to calculate the density of the superfluid condensate in liquid helium. It turns out that the density of particles in the condensate, as well as T0, depends on the ratio universal constants only [10]:

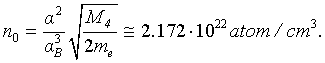(2)

(where a_B is the Bohr radius).

Since all helium atoms pass into condensate at a low temperature, then it is possible to calculate the density of the liquid helium:

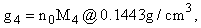(3)

which agrees well with the measured density of liquid helium equal to 0.145 g/cm³.

In helium-3 for the forming of the superfluid quantum ensemble, not only the zero-point oscillations should be ordered, but the magnetic moments of the nuclei should be ordered too. For this is necessary to lower the temperature below 0.001 K. This is also in agreement with experiment. Thus it is possible to show that both related super-phenomena superconductivity and superfluidity are based on the single physical mechanism the ordering of zero-point oscillations.

The Physics of Metals Thermomagnetic Effect

Among the theories of the twentieth century, there is another, which is based on an erroneous understanding of the mechanism of the considered phenomenon. The main subject of study of the physics of metals is the behavior of a gas of conduction electrons. The characteristic properties of metals their high thermal and electrical conductivity are due to the existence of free conduction electrons. In considering the mechanism of heat conduction in metals, it is assumed that the heat transfer is carried out by flow of hot electrons moving from the heated area of a metal in the cold one. This hot stream displaces the cold electrons, which are forced to flow in opposite direction. Since we are considering a homogeneous metal, the theory of this phenomenon assumes that these counter-currents flow diffusely. A flow of two diffuse counter-currents of equal magnitude suggests a complete absence of induced magnetic fields. This point of view on considered process established in the early twentieth century. On their basis, the theory of thermoelectric phenomena in metals was developed, which predicted full absence of thermomagnetic effect in metals. However, the thermomagnetic effect in metals exists [11], it is quite large and it can be easy found with the help of modern magnetometer.

The theoretical mistake arose from the fact that even in a completely homogeneous metal sample the counter-currents repel each other. As a result of the repulsion of opposite flows of hot and cold electrons in a metal arises their convection. It induces a magnetic field inside and in the vicinity of the sample. The corrected theory takes into account the thermomagnetic effect [12], fits well into the overall picture of thermal phenomena in metals.

Elementary Particle Physics

It is assumed that the basis of modern elementary particle physics is the quark model. The formation of this theory seems quite natural in the chain of sciences on the structure of matter: all substances consist of atoms and molecules. The central element of atom is nucleus. Nucleus consists of protons and neutrons, which in turn are composed of quarks. The quark model assumes that all elementary particles are composed of quarks. In order to describe all their diversity, the quarks must have a fractional electric charge (equal to 1/3 e or 2/3 e) and other discrete properties, referred to as flavor, color, etc. In the 60 years after the formulation of the foundations of the quark model, many experimenters sought to find particles with fractional charge. But to no avail. After that was coined by the confinement, ie property of quarks, prohibiting them in any way to express themselves in a free state. Once something like that happened in the European history. To some extent, this situation is reminiscent of the medieval concept of angels. Nobody doubted in an existence of angels, but they were attributed a property of the full indetectability. In modern physics, there is a handy method when nonexistent in nature particles are entered for convenience of description of certain phenomenon. For example, the phonons in crystals well describe many phenomena, but they are only the best method for studying these phenomena. Phonons are quasi-particles, ie, they do not really exist, but they are successful and convenient theoretical abstraction. If one treats the quarks also as quasi-particles, their existence does not require experimental evidence. At that the convenience and the accuracy of the description come to the fore for them. Really, the quark model aptly describes some experiments on the scattering of particles at high energies, for example, the formation of jets or a feature of the high-energy particles scattering of without their breaking. However, that is not very strong argument. The basic quarks of the first generation (u and d) are introduced in such a way that their combinations could explain the charge parameters of protons and neutrons. Naturally, the neutron is considered at that as an elementary particle in the sense that it consists of a different set of quark than a proton. In the 30s of the 20^th century, theoretical physicists have come to the conclusion that a neutron must be an elementary particle without relying on the measurement data, which was not at that time. Are there currently required measurements? Yes. The neutron magnetic moment and the energy of its beta-decay were measured and they can be calculated based on some model. Let us assume that a neutron is composed particle, and, as well as the Bohr’s hydrogen atom, it consists of a proton, around which on a very small distance, an electron rotates. On a very small distance from the proton, the electron motion becomes relativistic. As a result, the radius of the electron orbit is dependent only on the universal constants:

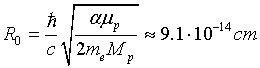(4)

Where 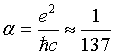is the constant of fine structure,

μ_p is magnetic moment of proton in Bohr magneton,

m_e and M_p are electron and proton masses.

In the result, the calculated value of the magnetic moment of a neutron depends only on the universal constants, and therefore it can be calculated with high precision [12]:

μ_n ≈ −1.91352. (5)

It’s great that the obtained estimation of the neutron magnetic moment is in very good agreement with its measured value:

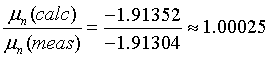(6)

Additionally, this result is supported by other calculation. In this approach, the interaction energy of a proton and an electron inside the neutron is found to be:

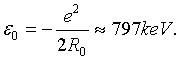(7)

At the decay of a neutron, this energy must go into the kinetic energy of the emitted electron (and antineutrinos). That is in quite satisfactory agreement with the experimentally determined boundary of the spectrum of the decay electrons approximately equal to 782 keV. This concept changes the approach to the problem of nucleon-nucleon scattering. The full nucleon-nucleon scattering consists of nuclear and Coulomb components with different angular dependencies. Given the fact that a neutron consists of a proton and surrounded it a relativistic electron cloud, nuclear component in all possible scattering combinations proton-proton, proton-neutron, neutron-neutron should be the same, the difference may consist only in the presence or an absence of the Coulomb contribution that is consistent within the errors with the measurement data. These arguments are irrelevant to other elementary particles and quarks with other properties. The obtained consent of the considered model with measurements says only that the proton and neutron must be described by the same set of subparticles.

Theoretical nuclear physics

With all the distinctive features of modern theoretical nuclear physics, it has something in common with the above disciplines astrophysics and theory of superconductivity. Nuclear physics in its present form explored many common patterns of nuclei. For example, the structure of shells, revealing the magic and nonmagic nuclei, etc. But just as the theory of superconductivity and astrophysics, nuclear physics is not taken for the prediction of the main properties of objects it studies. The most important property of an individual nucleus is their binding energy. The conduct of quantitative calculation of the binding energy of even the simplest nucleus fails. An alternative approach to the calculation of the binding energy of nuclei can be developed on the basis of the electromagnetic model of a neutron, discussed in the previous section. The first model of nuclear forces apparently was offered by Tamm IE [13] back in the 30s of the last century. He suggested that the occurrence of attraction between nuclear particles can be explained by an electron exchange. However, later in nuclear physics, the model of π-meson exchange has become the dominant. The reason for this is clear. To explain the value and range of the nuclear forces needs a heavy particle with a small own wavelength. An non-relativistic electron does not fit for it. However, on the other hand, the model π-meson exchange was not too productive. It cannot give a quantitative explanation of the binding energy of even simple nuclei. The quantummechanical model of the system in which the attraction force between two protons was arisen due to the electron exchange has been well studied. The solution to this problem was considered by F.London W.Heitler back in the late 20’s of the last century [14]. They showed that the exchange by electron between protons in the molecular ion of hydrogen caused forces of attraction of purely quantum-mechanical nature, which does not exist in classical physics. Naturally the attraction force between protons in the molecular ion in the Heitler-London model appeared at a distance of the order of the Bohr radius. The energy of this interaction has the order of the energy of an electron in a hydrogen atom. This theory can be easily reformulated for the case of exchange of relativistic electron in a pair of proton-neutron [12]. In this case, the range of this quantum force should be approximately equal to the characteristic radius of the neutron R₀ (4), and the energy of this interaction is of the order of ε₀ (7). In accordance with the London-Heitler theory, the electron exchange in the neutron-proton pair should lead to their attraction with the energy depends on the distance between the protons R. If to enter this distance in dimensionless form x = R/R₀, the London-Heitler exchange energy is equal to:

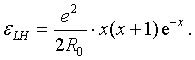(8)

Differentiation of this function with respect to x indicates on the existence of its maximum at x ≈1.62 and the maximum energy of attraction:

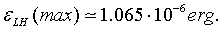(9)

To compare this energy with the experimental data, we must calculate the binding energy of all the particles, which causes the mass defect of the deuteron:

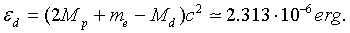(10)

One must subtract the neutron binding energy En from the full binding energy, because at the theoretical estimation we were interesting by the energy of proton-neutron pair. The binding energy is carried away at the neutron β-decay, i.e. ε_n = 782.32 keV. In result

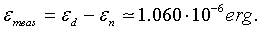(11)

This good agreement between the theoretical estimation ε_LH and measurement data is a clear proof that the so called strong interaction (at least in the case of the deuteron) is a manifestation of the attraction between protons produced by the exchange of relativistic electrons.

Conclusion

Thus, if, in principle, experimenters can carry out their measurements without regard to the theory, but theoretical studies must necessarily be based on data experimenters. Discussed above quasi-theories, are not confirmed by experiment, have some common features. Usually they use complicated mathematical apparatus, which cannot be simplified in order to obtain a simple, but physically accurate consideration of phenomenon in order of value. The main drawback of quasi-theories is that they cannot give an explanation of paramount individual properties of the objects. They try to explain the general characteristics of the phenomenon as such and reach agreement with experiment for properties, which can be often attributed to the thermodynamic. A lot of pseudo-theories exist now and a blame on that lies on special scientific journals in particular. It would seem to be all clear to them since they do not satisfy the main principle of the natural sciences. One might think that the editorial boards of scientific physics journals can be blamed in it. The most of reviewers in these journals are theorists naturally. Often they developed their own criterion of the correctness of a particular article. They believe in their own theories, and not allowed to publish articles that are not consistent with these theories, even if it is obvious that the models in these studies are consistent with the measured data. As these pseudo-theories violate the Gilbert’s-Galileo’s basic principle and, apparently, the editors of these journals need more strictly relate to them. Probably it makes sense to open special sections in journals which can be called, for example, as “Theoretical studies that do not yet satisfy at these their stages to the general principle of natural science.” In this case, readers and the Nobel Committee could easily develop a cautious attitude to these theories.

References

1. Gilbert W.De Magneto MagneticisqueCorporibusEt De MagnoMagneteTellure. There is the Russian edition. 1956.
2. Carroll BW, Ostlie DA. An Introduction to Modern Astrophysics. Reading.1996.
3. Padmanabhan T. Theoretical Astrophysics.2000; 1.
4. Vasiliev BV. Physics of Stars and Measurement Data Part I. Universal Journal of Physics and Application. 2014; 2: 257-262.
5. http://sohowww.nascom.nasa.gov/gallery/Helioseismology
6. Campbell WH. Earth Magnetism. AcademicPress. 2001.
7. Sirag SP. Nature.1979; 275: 535.
8. Blackett PMS. Nature. 1947; 159: 658.
9. Vasiliev BV.IlNuovoCimento B. 1999; 114B: 291-300.
10. Vasiliev BV.Superconductivity and Superfluidity. Science PG. 2015; 129.
11. Vasiliev BV. The New Thermo-magnetic Effect in Metals. Universal Journal of Physics and Application. 2014; 2: 221-225.
    
12. Vasiliev BV. About Nature of Nuclear Forces.Journal of Modern Physics.2015; 6: 648-659.
13. Tamm IE. Neutron-Proton Intaraction. Nature. 1934; 134: 1011.
14. Heitler W and London F. Wechselwirkung neutralerAtome und homopolare Bindung nach der Quantenmechanik. Zeitschrift fr Physik. 1927; 44: 455-472.