Proof of Legendre’s Conjecture

Abstract

A method is presented to prove Legendre’s conjecture based on identity that holds true for all numbers

Keywords

Legendre’s conjecture, Hypothesis

Introduction

The properties of prime numbers have been studied for many centuries. Euclid gave the first proof of infinity of primes. Euler gave a proof which connected primes to the zeta function. Then there was the Gauss and Legendre’s formulation of the prime number theorem and its proof by Hadamard and de la Vallee Poussin. Riemann further came with some hypothesis about the roots of the Riemann-zeta function [1,2].

Many others have contributed towards prime number theory.

Legendre’s conjecture, proposed by Adrien-Marie Legendre states that there is a prime number between n2 and (n+1)2 for every positive integer n. The conjecture is one of Landau’s problems (1912) on prime numbers. The conjecture has not been proved to the time of writing of this paper [3,4].

The Goldbach conjecture was proved in a paper entitled “a simple proof of Goldbach conjecture.

In this research a method will be presented of proving Legendre’s conjecture.

Methodology

From Legendre conjecture:

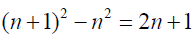(1)

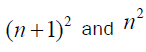are composite numbers with exceptional case where n=1.

Consider a prime number:

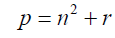(2)

Such that:

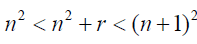(3)

From 3:

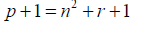
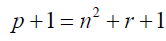(4)

When one is added to a prime number the result is an even number (e).

e = n² + r +1 (5)

According to Goldbach conjecture (proved) every even number greater than two is a sum of two prime numbers.

Therefore:

e ≥ 4 (6)

n =1 (7)

We consider the limit case n =1 and e ≥ 4 , then by equation 4, ( e ≥ 4 ).

For e ≥ 4

For odd primes p₂ and p₂ then interpreting equation 4 using Goldbach conjecture:

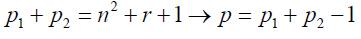(8)

From equation 2:

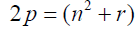(9)

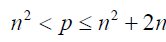
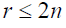
Goldbach conjecture states that every prime number greater than two is the sum of two prime numbers. Equation 9 borders on Goldbach conjecture. For the purpose of the present analysis we will rewrite the equation to suit our proof method [5-8].

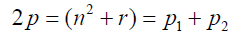(10)

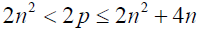(11)

Existence of a prime number between 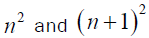also means existence of an even number twice the prime in the range ( 2n2 < 2 p ≤ 2n2 + 4n ). This implies in this range there should also be an even number that is twice a prime number. The effectively means if n is even r should be odd and versa [9,10].

Legendre’s conjecture implies the maximum gap between primes for numbers between 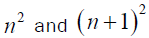is given by:

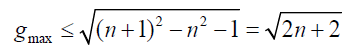(12)

This means the minimum number of primes from 1 to is given by:

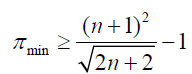(13)

Thus between 1 and 4:

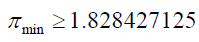
Between 1 and 9:

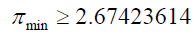
Between 1 and 100:

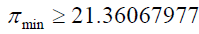
For numbers between 1 and one million:

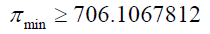
This means the minimum number of primes between 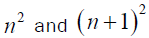is given by:

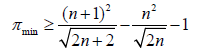(14)

For numbers between 1 and 4 the minimum number of primes is:

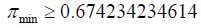
A positive fraction greater than zero would here implies that the number of primes between 1 and 4 is at least 1.

For numbers between 4 and 9 the minimum number of primes is given by:

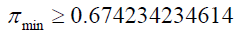
The number of primes is at least one.

For numbers between 81 and 100:

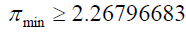
The number of primes is at least 3.

From equation 14 we can establish that there is at least one prime number between every consecutive pair of square numbers. This verifies Legendre’s conjecture.

References

1. (n.d.). Retrieved from http://www.math.dartmouth.edu/ euler/correspondence/letters/OO0765.pdf.
2. Conrey JB. (2003, March). Riemann Hypothesis. Retrieved 12 20, 2017, from https://www.aimath.org/WWWNrh/Lehman DJ. On Primality tests. SIAM Journal on Computing . 1982;374-375.
3. Manindra ANK. (Sep). Primes in P. Annals of Mathematics.2004;160,781-793.
4. Shanks WA. Strong Primality tests that are not sufficient. Math Comp.1982; 39:255-300.
5. Sinisalo MK. Checking Golbach conjecture upto 4×10¹¹. Math.Comp. 1993; 61:931 - 934.
6. Veisaidal J. (2016, August 22). Medium. Retrieved December 19, 2017, from Medium.com: https:/medium/com/@JorgenVeisal?source=Post
7. Veisdal J. (2015, August 22). Retrieved January 2017, from Medium: https://medium.com@JorgenVeisdal/the-riemann-hypothesis-explained-fa01c1f75d3f
8. Wang,Y. The Golbach Conjecture. World scientific vol. 2002;4 .
9. Weiststeien EW. (n.d.). Goldbach conjecture. Retrieved 11 22, 2017, from From MathWorld- AWolfram Web Resource: http://mathworld.wolfram.com/GoldbachConjecture..html