Research & Reviews: Journal of Pure and Applied Physics
MenuISSN: 2320-2459
ISSN: 2320-2459
Patricio Corbalan Campos1*, Luciano E. Chiang1
1Department of Mechanical & Metallurgical Engineering, Pontifical Catholic University of Chile, Santiago, Chile
Received: 10-May-2022 Manuscript No. JPAP-22-63918; Editor assigned: 13-May-2022 Pre QC No. JPAP-22-63918(PQ); Reviewed: 27-May-2022, QC No. JPAP-22-63918; Revised: 3-June-2022, Manuscript No. JPAP-22-63918(A) Published: 10-June-2022, DOI:10.4172/2320-2459.10.4.002
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
An effective method based on current signal (of stator current) monitoring in time is applied to diagnosis rotor unbalanced or eccentricity fault. This method can also determine the degree of severity of the fault, which is determined in eccentric mass or eccentric radius. The experiment consisted in amplitude of current signal monitoring for various masses and radius that were applied. The eccentricity fault was simulated through a mass that was fixed in a shaft fixed to pulley solidarity to the turbine shaft, in this way, the health condition was evaluated for different position of the mass and different masses. The results were analyzed in curve between current amplitude and eccentric mass or current amplitude and eccentric radius. In both cases, the obtained tendency was a linear model, which verified the physical model of this situation. Bayesian method can estimate the current signal amplitude associated with a specific combination of mass and radius, determining the severity of the fault. Bayesian method can isolate the signal and the noise. The Bayesian method permits to prognosis the state of the turbine through amplitude of the current signal monitoring. This method was studied in stationary conditions.
• This research studies rotor unbalance fault in wind turbines through current signal monitoring. Various eccentric masses were applied to the pulley of accomplishing of the motor and generator (PMSG) shafts with various eccentric radiuses. The fault was studied for various conditions and the results were summarized in a curve between current amplitude versus mass or current amplitude versus eccentric radius.
• A method based on Bayesian Inference (Metropolis-Hasting) is presented and evaluated in this research. The Bayesian methods permit to prognostic the state of the turbine through by posterior distribution of the current signal amplitude for specific mass and eccentric radius. Bayesian method provides information about uncertainty quantification in estimation of parameters.
• One of the most important contributions of this work is the estimation of signal noise through the application of the Bayesian Inference method.
• The frequency of generator shaft rotation is also determined by the application of the method. This magnitude can be compared with the measurement.
The renewables energies have acquired great interest since various years ago [1]. Particularly, the wind energy is one of the most important resources of renewable energy. Wind energy is based on energy transformation from the wind to electrical energy through a turbine. Wind turbine is a device which transforms energy from wind to mechanical energy (movement of the blades) and then, to electrical energy trough a generator, in this case PMSG. The geographical location of a wind turbine has a great impact in energy conversion process because the conversion process is given by wind conditions of the location. For this reason and others such as safety and minimization of the impact of noise pollution, wind turbines are usually found in remote locations. The turbines can be installed both onshore and offshore. In this context, the maintenance become very important since access to the turbines is very limited and it is determined by location, therefore, a corrective maintenance approach-replacement of the component after occurrence of a failure [2] could be not the most convenient approach. On the other hand, maintenance involves repair and replacement costs, for example, these associated with the unavailability of the turbines to generate energy. Preventive maintenance proposes a scheduled maintenance in which the replacement of component is linked with the hours of operation. In this case, it may be not necessary to replace or repair them; therefore, there is an unnecessary cost. Other way to overcome this challenge is a condition based on monitoring methodology. This methodology indicates when a component must be replaced or repaired before it fails and when it is close to doing so, thus avoiding unnecessary replacement of components [3].
In general terms, there are not many applications of Bayesian inference in determination of rotor unbalance. A method based on Markov Chain Monte Carlo was presented by Tyminski, et al. [4] in which the researchers studied a fault located on bearing through a mathematical model and the application of the method based on MCMC. In this research the same concept is applied but it is applied on rotor unbalance fault not on bearing fault. Taherkhani and Ahmadian [5] applied the same concept to diagnosis bearing fault. This paper adopts selection parameter procedure and sampling strategy for stochastic model updating to investigate variability in the dynamic behavior of a complex turbo compressor rotor-bearing-support system. Lawrence, et al. [6] presented a work in which bearing condition is estimated using Markov Chain Monte Carlo trough adaptive Metropolis-Hasting Method. In this camp there are few applications and the most of them applied to bearing condition, in this research a method based on Metropolis-Hasting algorithm of MCMC is applied to determine the severity of the rotor unbalance fault or eccentricity fault.
If the research is focused in the concept of eccentricity fault detection, there are many works. However, none of them applied MCMC to diagnosis eccentricity fault detection or rotor unbalance. Faiz and Moosavi [7] presented a complete review of eccentricity fault detection in induction machines. This publication exposes three types of eccentricity faults, static eccentricity, dynamic eccentricity, and mixed eccentricity. In the first one, rotational axis coincides with the rotor shaft, but it is displaced from stator shaft. In second, the rotational axis coincides with stator shaft, but not with rotor shaft. In the last one, the axis of rotation is different not coincides with none of them (rotor and stator shafts). In the case of this research, the eccentricity is a dynamic eccentricity because the description of this kind of fault is accomplished.
Ebrahimi and Faiz [8] proposed a technique to extract frequency pattern from magnetic field analysis to accuracy the fault recognition of eccentricity in a synchrony generator of permanent magnets (PMSG). In this analysis, the impact of slots, saturation and dynamic and static eccentricity are considered. Abu-Elhaija and Faiz [9] proposed an analytic approach to predict torque curves and instantaneous velocity of three-phase motor subjected to mixed eccentricity failure. This approach can be used to predict type and degree of eccentricity using electromotive forces of the three phases for a failure of mixed eccentricity in which slot and saturation effects are considered. The calculation is based on analytic solution of equations of field of cylindrical coordinates using Laplace and Poisson equations. Torkaman and Afjei [10] determined the degree of freedom for eccentricity fault in switched reluctance motor based on non-linear function of static torque to minimize the wave of torque for maximum performance in the monitoring operation. An algorithm of a non-linear torque function versus rotor position and percentage of eccentricity of the motor to operation of switched reluctance motor was introduced. The switched motor reluctance was analyzed first through three-dimensional finite element method to estimate non-linear torque function and then, the function is approximated by least squared, cubic spline and Hermitian cubic methods. The minimization is performed through a search algorithm and genetic algorithm. Ebrahimi, et al. [11] presented an approach to detect dynamic eccentricity in a rotor of a synchrony motor. This objective is reached through an efficiency index based on torque processing by a method based on data mining in time series. Faiz and Ojaghi [12] introduced an index to diagnosis eccentricity fault in squirrel cage motors. Babei, et al. [13] proposed a detailed model of synchrony generator of salient poles over dynamic eccentricity, which is capable of accuracies the magnetic saturation effects, relevance of shoes of pole of the rotor, and the spacing of distribution of the stator phases and rotor winding. The variation of result of the air gap distribution in presence of eccentricity fault in accuracy calculated and the function of the air gap is computed using Fourier series. Mirimani, et al. [14] studied the effects of static eccentricity in axial flux machines of permanents magnets applying the finite element method. Samaga and Vittal [15] modeled an eccentricity fault of the induction motor air gap applying multiple circuit approach and theoretical function of winding 2D modified. A novel method of detection of fault severity based on covariance analysis was presented to predict the degree of deterioration of health state of a machine by eccentricity of air gap. Akar [16] developed a new method to detect static eccentricity fault in a closed loop operating an induction motor controlled by inverter. In this methodology the phase current and velocity of the rotor were monitored for several velocities and load levels in the health condition and in the fault condition of static eccentricity in close loop of induction motor. The principal innovation of this study is that the AD-OT method was implemented in the current signal for first time. Torkaman and Afjei [17] presented an exhaustive method to diagnosis eccentricity faults in a reluctance machine switched during offline and repose modes. This methodology employed a transient finite elements method to analyze the situation and the results are validated through experimental tests on a prototype machine in laboratory. This method permits to estimate severity of fault. Halem, et al. [18] proposed that the amplitude of components of characteristic frequency with low degree of static eccentricity is detected using flux magnetic analysis of airgap. Karami, et al. [19] studied static eccentricity in a three-phase motor. The analytical expression of permeability and the components of non-uniform air gap flux due to static eccentricity failure were discussed. Ebrahimi, et al. [20] computed novel index to diagnosis eccentricity fault (dynamic and static) in permanent synchronous magnet motors. The index is a linear combination of energy, shape factor, peak, angle of head of peak, area below peak, gradient of peak, wavelet decomposition of signals, and coefficients of autoregressive model, which are obtained from stator current. This method uses vectorial supported machine to classify the results. This methodology applied the finite element method to model PMSM with eccentricity fault and to calculate the current of stator signal. Finally, this method estimated the severity of the fault, which always has been ignored in previous studies. Mirimani, et al. [21] researched an online method to detect static eccentricity of machines of single axial flux of rotor. This methodology permits both the estimation of static eccentricity factor and the calculation of minimum position of air gap. Siddiqui, et al. [22] proposed a technique to diagnosis early faults of air gap. The air gap failure can be diagnosed in transient condition before to become a catastrophic fault. In this research, a model of induction motor actioned by an inverter has been proposed. This methodology permits to diagnosis eccentricity fault of air gap in transient condition in time domain and frequency domain. Naderi, et al. [23] analyzed the torque wave, considering both the opening of the slot and the winding effect for a machine of synchrony reluctance of 4 poles and 60 slots in healthy and eccentricity conditions. This paper proposed ma method to diagnosis dynamic and static eccentricity faults using the vibration signal. Faiz, et al. [24] performed three-dimensional modeling of induction motor using magnetic equivalent circuit. Ounmaar, et al. [25] presented an alternative method based on analysis of neutral line of voltage to detect the eccentricity of air gap, and to highlight the classification of all harmonics RSH in the neutral line of voltage. This is a model of squirrel cage induction motor based on geometry of the rotor and in the design of winding. This model was used to analyze the impact of static eccentricity of air gap through prediction of relative frequencies in the neutral line of voltage spectrum. Li, et al. [26] proposed a technique of intelligent harmonic synthesis to perform an incipient fault detection of air gap eccentricity in induction motors. Safa, et al. [27] proposed an index to detect static eccentricity, dynamic eccentricity, and mixed eccentricity in permanent magnet three-phase generator (PMSG). The proposal index is the amplitude of the component of side band with pattern of frequency which is extracted from the stator voltage spectrum. Finite element method is applied to model PMSG with eccentricity fault and to compute the voltage of stator as appropriate signal for processing. In this publication, finite element method is used to study the magnetic field in the PMSG using a wind turbine. The main advantage of this method over other methods in the literature is that is capable to diagnosis eccentricity fault in a non-load state before that generator presents damage. Hassanzadeh, et al. [28] presented a modeling method of static eccentricity effects, dynamic eccentricity and mixed eccentricity based on electromotive force in the mounted surface in permanent magnet. In this work, the impact of eccentricity fault in magnetic flux distribution is addressed.
In this research, a generator of wind turbine under dynamic eccentricity in stationary conditions is studied. The fault is simulated through different masses in different positions (radius) in the system. The system permits the change of the mass and position of the mass. The eccentricity fault and its severity are diagnosed by acquisition and processing of the current signal, specifically amplitude of current signal. Current signal in eccentricity condition is a sinusoidal signal. The current signal is modeled by mathematical model that consists in linear relationship between current amplitude and mass and radius. This research applies Bayesian inference method to calculate the amplitude of the current for first time and provides information about uncertainty quantification in the estimation of the parameters of the model. The principal contribution of this research is that is possible to obtain the degree of severity of the rotor unbalance or eccentricity fault. For each combination of mass and radius was obtained amplitude of current characteristic with linear relationship between current amplitude and independents variables (mass and radius). Other contribution is that is possible to isolate the noise of the signal and to estimate the magnitude of noise (Table 1).
 |
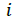Current of stator rectified |
 |
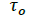Stationary component of torque (provided by the motor) |
 |
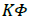Parameter of the generator (relationship between torque and current) |
 |
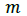Eccentric mass |
 |
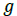Gravity acceleration |
 |
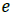Eccentric radius |
 |
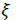Factor of difference between oscillatory component of torque in motor |
 |
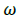Angular frequency of rotation of eccentric mass (angular velocity of the system) |
Table 1. Nomenclature used.
Experimental design
The experiment has a simple structure. PMSG characteristic are described in Hernández, Chiang and Corbalán [29]. The most important characteristic for this configuration is that the parameter KΦ is 0.219 (Vs). This value is close to 0.23 (Vs) (the measured value in the experiment). The experiment consists in PMSG which contains a shaft in which the eccentric mass can be displaced through the shaft fixed to pulley Figure 1. The mass is fixed by nuts to the shaft, which is fixed to pulley. The eccentric mass can be displaced trough the shaft; therefore, the device can be evaluated in different positions of the mass. PMSG is connected to electrical motor through a strap as is observed in the picture. The rotational velocity is measured on pulley through a sensor that reads reflective paper fixed on the pulley and it is a constant value close to 90 rpm approximate in each measurement. Different masses can be added in the device at different radius. These are the independent variables, and the current signal is the dependent variable.
Figure 1: PMSG with eccentricity mass.
Voltage signal is measured by oscilloscope whose terminals are connected to resistor terminals Figure 2 and current signal is obtained by Ohm’s law through resistor value. The resistor is connected to rectifier dc terminals. The rotor of the generator rotates with constant rotational velocity in this research. In this situation the torque provided by air in the turbine, is provided by the electric motor, therefore, the torque has stationary component and oscillatory component provided by eccentricity effect.
Figure 2: Circuit of the system.
Mathematical model for detection of eccentricity failure
The proposal model is based on physics of the system which represents the output current of the system (current generated by generator) and its relationship with electrical torque. The advantage of this model is that accounts the physics of the system using a simple mathematical relationship between the main variables, reducing the number of sensors, and increasing reliability of the system which is rotating with constant speed. The parameters of the model are computed by Bayesian inference method. The model is applied in stationary conditions.
The mathematical model involves current signal of the stator of PMSG, electric torque signal, eccentric mass and eccentric radius. In a wind turbine the torque of air is generated by the movement of the blades. In this research the torque of wind is generated by electrical motor, and for this reason the torque is an electrical torque. The electrical torque generates the movement of the turbine shaft, therefore, generates electrical torque of the turbine provided by current flowing in the system. Furthermore, there is a contribution of mass and radius of eccentricity. The mathematical formula which involves these variables is
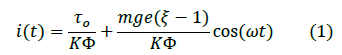
Bayesian inference method (MCMC Metropolis-Hasting)
The amplitude of the current in model (1) is computed through a Bayesian inference method based on Markov Chain Monte Carlo, specifically through Metropolis-Hasting algorithm. This method permits to perform uncertainty quantification in the parameters, give some data. This uncertainty quantification can be performed using Bayes theorem:
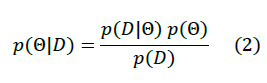
Where θ represents the model parameters and D represents the data. The terms of Bayes theorem are the following:.
• 
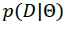: Likelihood probability. This function contains the information about how likely is that some model parameters explain the data.
• 
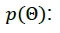The prior probability. This probability contains the information a prior knowledge about the model parameters.
• 
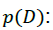The prior probability. This probability contains the information a prior knowledge about the model parameters.
• 
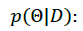Posterior probability. This probability provides information about the parameters given the data.
Metropolis-Hastings computes the posterior probability in relative terms:
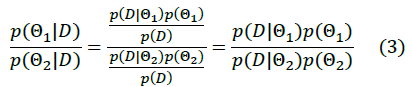
In this way, the algorithm avoids the computation of the evidence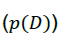 
which is difficult and expensive. The algorithm starts with an initial guess, a new sample could be generated and add it if has more posterior probability than the current sample. These methods require includes samples in other directions because with this approach we will soon reach the maximum a posteriori and will get stuck there. To achieve this, we will define an acceptance probability.
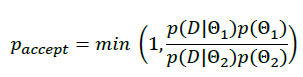
The next sample will be accepted randomly according to this probability. Note that if the new sample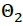 
has higher posterior probability than 
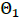, then 
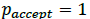and this sample always will be included.
The last part is how to generate a new sample, we will apply Markov Chain. The most common approach is to use Gaussian step.
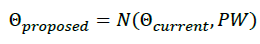
Where is the proposal width, which is a parameter that will influence the performance of the method.
For simplicity, the equation (1) will be written as:
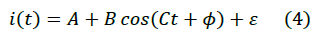
Figure 3 shows the signals for various rotational velocities without eccentric mass. The signals are planes in this case. On the other hand, Figure 4 shows the signals with eccentric mass (0.5 kg) at 0.17 m and at various rotational velocities. The comparison between both figures shows that signals with eccentric mass added are sinusoidal and it is possible describe them through an amplitude and a frequency.
Figure 3: Current signal for different velocities without eccentricity. 
Figure 4: Current signal for different velocities with eccentricity of 0.5 kg and 0.17 m. 
Figures 5-9 shows the estimation of parameter in each case. The estimated parameters are offset, amplitude, frequency, and noise. The current amplitude varies linearly with the eccentric mass. The frequency parameter is relatively fixed because the angular velocity of the electric motor was constant and the same (90 rpm). The offset parameter is the constant in which is displaced the function from X axis. This parameter is a constant because is given by the velocity of system. Finally, it was possible to estimate the noise of the signal.
Figure 5: Estimated parameter for current signal at 0.012 kg, 90 rpm and 0.170 m.
Figure 6: Estimated parameter for current signal at 0.192 kg, 90 rpm and 0.170 m
Figure 7: Estimated parameter for current signal at 0.400 kg, 90 rpm and 0.170 m.
Figure 8: Estimated parameter for current signal at 0.600 kg, 90 rpm and 0.170 m.
Figure 9: Estimated parameter for current at 0.800 kg, 90 rpm and 0.170 m.
Figures 10-14 shows data and model approximation in each case with respective estimated parameters. In each case the picture shows the sinusoidal function associated with the signal. It is possible to observe that the current amplitude grows with the mass at intervals of 0.200 kg this is clear. The model employed to approximate the signal (4) is sinusoidal, but the signal is not perfectly sinusoidal, for this reason the approximation of amplitude is not perfect, and this method estimates minor amplitude than the signal amplitude in Figures 12-14.
Figure 10: Current model evaluated at 0.012 kg, 90 rpm and 0.170 m.
Figure 11: Current model evaluated at 0.192 kg, 90 rpm and 0.170 m.
Figure 12: Current model evaluated at 0.400 kg, 90 rpm and 0.170 m. 
Figure 13: Estimated parameters for current signal at 0.600 kg, 90 rpm and 0.170 m. 
m=0.600 kg
Figure 14: Estimated parameters for current signal at 0.800 kg, 90 rpm and 0.170.
m=0.800 kg
Figure 15 shows the group of approximated signals for each mass at 0.170 m. This picture shows clearly that the current amplitude is influenced directly by the mass added to the system. In this picture also can be appreciated the frequency which is practically the same and the offset that is practically the same. On Figure 16, theses combinations of parameters are the red points, theses points form practically a linear model. The green points on Figure 16 are intermediate points. These points have a linear tendency with the growth of eccentric mass, but this tendency is minus pronounced that the tendency of the red points. This fact is explained in part because the signal is not perfectly sinusoidal, and the model employed in Bayesian inference is perfectly sinusoidal and there is a difference of accuracy in this case. The second reason is that the signal has not a pronounced change as red points. The transition of the stated is not pronounced for intermediate masses chosen.
Figure 15: Comparison between model with different mass at 0.170 m and 90 rpm.
Figure 16: Summary of current amplitude for different masses at 0.170 m. 
Model
On Figure 17 is viewed the relationship between current amplitude and eccentric radius at 0.192 kg. It is viewed that the tendency verifies the model (1) because is a linear dependency. Some points manifest the problem of accuracy given by difference between the signal and perfectly sinusoidal model, but they are fewer than Figure 16.
Figure 17: Current amplitude for different radius at 0.192 kg. Note:
The first conclusion is that the tendencies of variation of the current amplitude with the eccentric mass and eccentric radius confirm the model (1), in which the current amplitude depends linearly in both variables.
The method proposed in this research can estimate the current parameters. It was possible to estimate the noise of the signal in each case which is very important because the signal is very noisy. Both things mentioned before permit to diagnosis the fault and the degree of severity. Futures works will be incorporate to improve the accuracy of this method.