Research & Reviews: Journal of Pure and Applied Physics
MenuISSN: 2320-2459
ISSN: 2320-2459
Marieam Ghreeb Jasim and Qusay Adnan Abbas*
Department of Physics, College of Science, University of Baghdad, Baghdad, Iraq
Received Date: 18/09/2018; Accepted Date: 23/10/2018; Published Date: 30/10/2018
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
Laser-induced breakdown spectroscopy of CuO plasma in the presence and absence of magnetic field has been investigated. The plasma was generated by employing Nd: YAG laser (532 nm, 9 ns) at various pulse laser energy ranging from 100 to 400 mj in a vacuum. The increasing of pulse laser energy in the presence and absence of the magnetic field had shown increasing in electron density while the electron temperature was decreases. The presence of the magnetic field cause to a rising the electron density but it reduces the electron temperature comparison with the case of absence of the magnetic field. According to theβ value distribution along the target, the results shows in the central region of the target the plasma plump that produced by laser is in a good confinement in this region in contrasted with edge region of the target region.
Laser-induced breakdown spectroscopy (LIBS) is an analytical technique based on the application of one or more high power laser pulses on a reduced region of the sample surface, promoting ablation and excitation of the specimen with the formation of a transient plasma. In the technique, the emitted radiation is associated with the sample chemical composition and is monitored by means of an appropriate detection system (wavelength selector and detector) [1]. Laser-produced plasma is transient in nature with characteristic parameters that evolve quickly and are strongly dependent on irradiation conditions such as incident laser Intensity and pulse duration, laser wavelength, irradiation spot size, ambient gas composition, and ambient pressure [2,3]. In recent years, the use of the magnetic field to confine the laser-produced plasma has become significantly important. The magnetic field can be used to control the dynamical properties of transient and energetic plasmas inefficient ways. The high-intensity pulsed magnetic fields have been found useful in enhancing the emission from laser-induced breakdown plasma [4]. The expansion of laser-induced plasma in the presence of magnetic field may initiate several physical phenomena including plume confinement, Joule heating effect, conversion of plasma thermal energy into kinetic energy, plasma instabilities, emission enhancement [5]. Dynamics of laser-produced plasma play an important role in deciding the characteristics of the plasma [6-8]. The degree of plasma confinement was in good agreement with simple magnetohydrodynamic (MHD) modeling [9]. Optical Emission Spectroscopy (OES) has been used for years to determine the plasma parameters such as electron density (ne), electron temperature (Te) and plasma frequency ωp [7]. The electron density in general, specifies the state of thermo- dynamical equilibrium of the plasma, while the temperature determines the strength of the different distribution functions describing the plasma state. The electron temperature of plasma was calculated using Boltzmann plot method [8]:
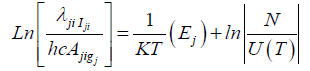(1)
where Iji is the relative intensity (in arbitrary units) of the emission line between the energy levels i and j, λji its wavelength (in
nanometres), gi is the degeneracy or statistical weight of the emitting upper level i of the studied transition, and Aji is the transition probability for spontaneous radiative emission from the level i to the lower level j. Finally, Ej is the excitation energy (in eV) of level
i, k is the Boltzmann constant, N state population densities. The electron temperature can be calculated from the slope of best
linear fit in the plot between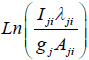 
versus Ej. This plot called Boltzmann plot.
In optical spectrum the line broadening can be explained by many fundamental such as the Stark broadening, Doppler broadening, and pressure broadening. The Doppler broadening and ionic broadening is so small that can be neglected. So the electron density can be calculated, using stark broadening relation, assuming it is the dominant effect for broadening [9]:
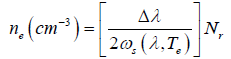(2)
Where Δλ is the FWHM of the line, and ωs is the Stark broadening parameter, that can be found in the standard tables Nr is the reference electron density which equal to 1016 (cm–3) for neutral atoms and 1017 (cm–3) for singly charged ions.
The Plasma frequency can be given as [10]:
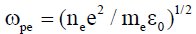(3)
Where ε0 is the electric constant, me is the electron mass, ne is the electron number density and e is electron charge. One of the important plasma parameter β, which is the ratio of plasma thermal pressure (kinetic energy) and magnetic field pressure (magnetic energy), is also evaluated:
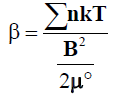(4)
Where K is the Boltzmann constant, ne is the electron density, B is the magnetic field intensity and Te is the electron temperature [11].
Figure 1 illustrated the experimental setup of LIBS system used for the detection and identification of spectral lines of laserproduced CuO plasma in the presence and absence of magnetic field. The target was bombarded by Nd: YAG pulses laser (9 ns duration time, 6 Hz frequency, and wavelength of 532 nm) with pulse energy ranging from 100 to 400 mJ which was used as an irradiation target for the generation of CuO plasma, at an angle of 45°. The laser was focused on target by using the convex lens of focal length 10 cm to produce plasma plume. The circularly shaped pellet of the copper oxide target with diameter 3 cm is placed inside a vacuum chamber. Argon gas was filled the chamber at a pressure at different pressure (from 0.2 and 0.4 Torr) which was measured by aprecisionable pressure gauge. The vacuum chamber consisted from a cylindrical stainless steel tube. The two ends closed by Pyrex windows, by two stainless steel flanges, and with small quartz window fixed in it is center, that allows for a laser pulse to shoot the CuO target. Two small pipes connected to pumping systems, while the other was used to deliver the argon gas (with purity of 99.9%).Two types of the permanent magnetic located under the target; the first one is the outer and the second is the inner which is located inside the outer circular permanent to get on the magnetic field intensity [12].
Figure 1: The experimental setup of LIBS system.
Figure 2 shows the radial profile of the magnetic field distribution along the CuO target. One can observe from this figure, the magnetic field intensity has nonuniform distribution along the target. It is clear from this figure the radial profile on the magnetic field along the target is non-uniform. The magnetic field intensity has two peaks which has the maximum value is approximately 41 mT.
Figure 2: The magnetic field distribution as function along the CuO target.
Effect of Magnetic Field on the Electron Temperature
The values of Te is calculated by using the Boltzmann plot method (Equation (1)) and are plotted in Figure 3. Many features can be observed from this figure which are; the electron temperature decreasing with increasing of gas pressure in the presences and absence of a magnetic field.The electron temperature increase in the presence of a magnetic field. The increasing of inelastic collisions of an electron with Ar atoms with increasing of gas pressure is responsible for decreasing of Te with increasing of pressure. While the increasing of Te in the presence of a magnetic field can be explained as, the magnetic field will traps the electrons in the region near the target surface. Therefore, the electron will gain the energy from the laser pulse and this will continue increases the electron temperature.
Figure 3: The variation of electron temperature as a function of pressure in the presence and absence of magnetic field.
Effect of the Magnetic Field on the Electron Density
Figure 4 had shown the variation of electron density (ne) versus gas pressure at different pulse laser energy in the presence and absence of the magnetic field. One can observe in this figure that the electron density increasing with increasing of gas pressure with higher rate in the presence of magnetic field for all pulse laser energy. The increasing of ne with increasing of gas pressure may be due to the inelastic collisions of electrons with Ar atoms which generated more electrons. On the other hand, the arising of the value of ne in the presence of magnetic field may be caused by the magnetic field will confinement the electrons and these electrons will suffered inelastic collision with Ar atoms then the secondary electrons will be generated more.
Figure 4: The variation of electron density versus gas pressure in the presence and absence of magnetic field.
Variation of β Value with Laser Energy
The values of β are evaluated by using eqn. (4) with Figures 3 and 4. Figure 5 illustrated the radial profile of the β value at different pulse laser energy and gas pressure. Many features can be observed in this figure; the values of β are less than on in all radial point in the region near the target surface. The maximum values of β occur at the edge of target. The increasing of pulse laser energy causes to increasing of β values. While the increasing of gas pressure causes to decreasing of β values. So that, one can concluded that from these results the fact that; according to the magnetic field configuration the magnetic field has a good confinement in the central region of the target (region of low β region) where the magnetic field pressure greater than plasma pressure.
Figure 5: The beta plasma profile aloge the Copper oxide target at different pulse laser energy.
The plasma characteristics that produced from the interaction of Q-Switching Nd: YAG laser at wavelength of 532 nm with solid CuO target in vacuum was studied. this work included the influence of pulse laser energy on the electron temperature, electron density and β parameter. One can observe in the presence and absence of magnetic field, when the pulse laser energy was increased the electron temperature was decreased while the electron density increased. While according to the β value distribution along the CuO target the results show the fact that the magnetic field has a good confinement in the central region of the target (region of low β region) where the magnetic field pressure greater than plasma pressure.