Stochastic Local Operations and Classical Communication (SLOCC) Entanglement Classification for 4n Qubits via Integer Partitions: A Commentary

About The Study

Quantum entanglement is a crucial quantum mechanical resource in quantum information theory. For example in quantum computation, quantum communication, quantum teleportation, quantum cryptography, quantum dense coding and so on. Many efforts have contributed to studying the different ways of entanglement. An important task of the entanglement theory is to classify different types of entanglement, for example LOCC, SLOCC and LU classification. It is well known that states belonging to the same SLOCC class can be used to do the same tasks in QIT with non-zero success probabilities. It is also well known that two-qubit states were divided into two SLOCC classes, and three-qubit states were classified into six SLOCC classes [1]. Though the entanglement for two and three qubits is deeply studied, it is hard to classify multipartite entanglement. In four-qubit states are classified into nine families under SLOCC [2].

For SLOCC classification of n qubits, it is important to find a SLOCC invariant which is used to classify states into a finite number of families. The previous articles proposed many SLOCC invariants: for example, the concurrence for two qubits, 3-tangle and local ranks of reduced densities for three qubits [1]. The degeneracy configuration for a symmetric state, ranks of matrices whose entries are coefficients of states: the entanglement polytopes, Jordan normal forms and spectra of coefficient matrices.

For entanglement classifications and measures for n qubits, recently, many efforts have been devoted to find SLOCC invariant polynomials. The SLOCC invariant polynomials of degree 2 for even n qubits and of degrees 4 and 6 for n≥ 4 qubits were proposed.

This commentary is made for SLOCC entanglement classification of 4n Qubits via integer partitions in [3].

It is well known that n-qubit pure state 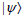and 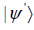are SLOCC equivalent if and only if there is an invertible local operator such that[1]

Let 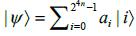be any pure state of 4n quibts, where 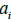are coefficients. Let 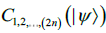be the 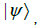coefficient matrix of 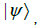where qubits 1,2,…, (2n) are chosen as row bits while qubits (2n+1), …., (4n) are chosen as column bits. Clearly,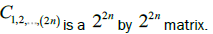

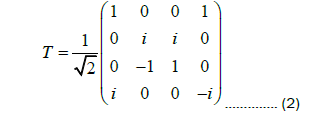
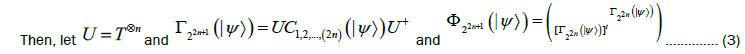
Here, we define that two Jordan normal forms 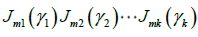and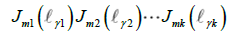 where 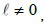are proportional. For example, 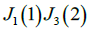and 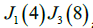are proportional. Then, we conclude the following form [3].

If the states 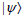and 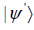of 4n qubits are equivalent under SLOCC, then spectra and Jordan normal forms of 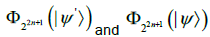are proportional, respectively.

For 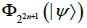, under SLOCC, its algebraic multiplicities, geometric multiplicities and sizes of Jordan blocks of are invariant.

We can classify spectra of matrices 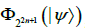and pure states of 4n qubits via integer partitions as follows. It is not hard to see that the spectra of 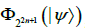are of the following form: 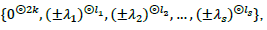where 2k, 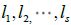are the algebraic multiplicities. Clearly, 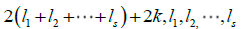.One can see that 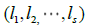is just an integer partition of the number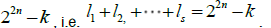

We define that spectra of matrices 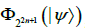belong to the same type if the spectra have the same algebraic multiplicities. By letting states with the same type of spectra of 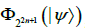belong to the same group, then SLOCC entanglement classification of 4n qubits is reduced to integer partitions of the number 2²ⁿ-k for each k, where 0≤ 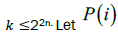be the number of integer partitions of i . For all k, there are 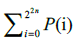different integer partitions. It means that we can classify pure states of 4n qubits into 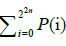different groups under SLOCC.

For example, spectra of 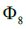and pure states of four qubits can be classified via integer partitions of 4-k as follows. First compute integer partitions of 4-k for each k, where 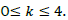for example, for k=1, integer partitions of 3 are 1+1+1, 2+1+3. Thus, for four qubits there are 12 integer partition, 12 types of spectra of 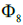and 12 groups of pure states without considering permutations of qubits.

We next show how to classify Jordan normal forms of matrices 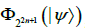via integer partitions of algebraic multiplicities. Let 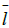stand for a set of all the integer partitions of l. for example,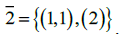Then, for each integer partition 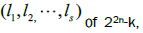we compute integer partitions 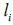and 2k. Let 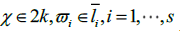Then, the list of partitions 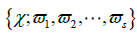is related to a collection of sets of sizes of Jordan blocks of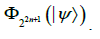

We next demonstrate that pure states of 4n qubits can also be classified via integer partitions of algebraic multiplicities. By letting states with the same type of Jordan normal forms of 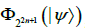belong to the same family, then SLOCC classification of 4n qubits is reduced to computing integer partitions of algebraic multiplicities.

References

1. Dür W, et al. Three qubits can be entangled in two in- equivalent ways. Phys Rev A. 2000;62:062314.

   [Crossref] [Google Scholar]

2. Verstraete F, et al. Four qubits can be entangled in nine different ways. Phys Rev A 2002;65:052112.

   [Crossref] [Google Scholar]

3. Li D Entanglement classification via integer partitions, quantum information processing Quantum Inf Process. 2020;19:21 .

   [Crossref] [Google Scholar]