Structural properties of ZnxCd1-xTe (x= 0.25, 0.50 and 0.75) ternary nanorods: Molecular Dynamics Simulations

Abstract

The structural properties of ZnxCd1-xTe ternary nanorods for (x= 0.25, 0.50 and 0.75) have been investigated by performing classical molecular dynamics simulations at various temperatures. An atomistic many-body potential energy function has been used to represent the interparticle interactions. It has been found that the structural properties of ZnxCd1-xTe ternary nanorods show a dependence on stoichiometry and temperature.

Keywords

ZnCdTe nanorods; atomistic potential; molecular dynamics.

Introduction

ZnCdTe, a ternary II-VI compound semiconductor that is used in a variety of technologies has been given much attention in recent years due to its adequate properties. The crystal which has excellent photoelectric properties and an high atomic number is promising semiconductor material used in space astronomy, environmental monitoring, homeland security and high resolution x-ray and γ-ray detectors for medical imaging applications at room temperature [1,2,3,4]. Moreover, the ZnxCd1-xTe alloy crystals have widely attracted among semiconductor materials with higher resistivity, which renders low noise level due to its applications in optoelectronic devices [5,6] and solar cells [7]. CZT nanowire sensors have been studied for detection of low energy γ-ray detection [8]. Zn_xCd_1-xT_e alloyed nanocrystals with different compositions have been synthesized in an aqueous solution with thioglycolic acid (TGA) as a stabilizer [9].

One-dimensional nanostructures, such as nanowires, nanorods and nanobelts, have received a great deal of attention over the past few years, especially ZnxCd1-xTe and ZnTe and CdTe strusctures. Recently, the optical properties of the obtained CZT nanorods have been investigated by photoluminescence (PL) spectroscopy with different refluxing times [10]. CdxZn1-xTe nanowires have been performed through control of growth temperature and using vapor-liquid-solid (VLS) method [11]. A VLS approach and template synthesis techniques have been reported for the preparation of ZnTe nanowires [12,13,14]. The electrical properties of ZnTe nanowires have been also measured at temperature range 15–100 °C [15]. Moreover, various liquid phase and template-assisted synthesis techniques have been reported for the preparation of CdTe nanowires [16,17,18]. Presently, it has been observed that ZnCdTe crystal will be the future technology that will allow the development of the next-generation of x-ray inspection and imaging systems that are required for a number of applications such as non-destructive inspection and testing of manufactured goods, as well as x-ray food inspection and x-ray fluorescence. Therefore, it is important to understand the structural properties of the material at various temperatures.

Molecular dynamics (MD) simulation is a powerful method used to study the properties at the macroscopic level based on information at the microscopic level. A computer simulation offers a route to investigate the material behavior at extreme temperatures which are difficult to realize in experiments. In this study, we have investigated theoretically mixed ZnxCd_1-xT_e nanorods representing solid solutions of the (ZnTe)_x and (CdTe)_1-x compounds for three compositions with x = 0.25, 0.50 and 0.75 using classical moleculardynamics simulations at different temperatures with the aid of atomistic many-body potential energy functions (PEFs). These compounds form a complete series of solid solutions with a cubic Zinc Blende structure with a direct energy gap. Zn_xCd_1-x Te nanorods are formed by the replacement of some of the Zn atoms in the ZnTe lattice with Cd atoms. The Zn and Cd concentration profiles determine the homogeneity of these mixed crystals. The present study is expected to be useful for understanding the influence of material structure on its properties and to offer relevant information for both experimental and theoretical research.

The method of calculations

In the molecular dynamics (MD) calculations, a many-body PEF, which is a linear combination of a two-body and three-body interactions, has been considered to perform total energy calculation. The two-body interactions U_ij are described by the Lennard–Jones function [19], whereas the three-body interactions (W_ijk) are described by the Axilrod-Teller triple-dipole function [20]. The explicit form of the total interaction potential energy of the system considered is given by

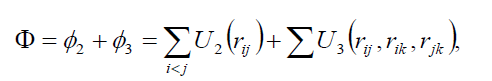      (1)

where U₂ and U₃ are the total two and three-body interaction potential energies, respectively,

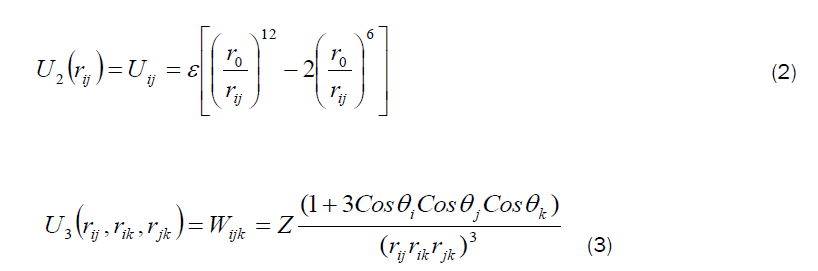
A similar PEF with a different set of parameters has been used to study the structural properties and energetics of Zn, Cd, and ZnCd clusters [21,22,23] and also to simulate the bulk, surface, and cluster properties of Si, GaAs and AlGaAs, SiGaAs, AuGaAs, SiC and SiO [24, 25,26,27,28,29], the cluster properties of AlTiNi systems [30,31], the structural properties of silicene nanoribbons (SiNRs) [32] and also the structural properties of Si nanorods [33].

The potential parameters used in the present study are shown in Table 1. The parametrization of the present PEF is given in detail in Ref. [21] for Zn, Cd, ZnCd. In addition to this, in the present study we have determined the potential parameters for Te, ZnTe, and CdTe systems to investigate the structural properties and energetics of Zn_xCd_1-xTe nanorods. The aim of the present study is, therefore, to investigate the structural properties and energetics of Zn_xCd_1-xTe nanorods for (x= 0.25, 0.50 and 0.75) at various temperatures. The simulations were carried out using the Nordsieck–Gear algorithm [37, 38] and predictor-corrector method [39]. The simulation initially started at 1K. Simulation cells of a size corresponding to an 1×1×1 unit cell consisting of 8 atoms were created. ZnxCd1-xTe ternary nanorods possess a cubic structure with a lattice constant of 5.708 Å (see Figure 1). Particle velocities were generated according to Maxwell-Bolztmann velocity distribution. In order to solve the equation of motion, the Nordsieck-Gear algorithm with a time step of 1.0 fs were used. The cut-off radius of 7.0 Å was used for maximum interaction range. A periodic boundary condition was imposed along the rod axis (z-axis in our case). The temperature ranges are as the follows: 1 K and 1500 K for Zn_0.25Cd_0.75Te, 1 K and 1800 K for Zn_0.50Cd_0.50Te, and 1 K and 2100 K for Zn_0.75Cd_0.25Te. The systems are relaxed until they reach equilibrium energetically. Depending on the composition and temperature the range of relaxation time varies as follows: Initially, Zn_0.25Cd_0.75Te, Zn_0.50Cd_0.50Te and Zn_0.75Cd_0.25Te nanorods were equilibrated in 45000, 30000 and 40000 time steps at 1K respectively. After that, time steps for Zn_0.25Cd_0.75Te, Zn_0.50Cd_0.50Te and Zn_0.75Cd_0.25Te are obtained by time averaging 300.000, 160.000 and 250.000 between 300K and 2100K separately. The initial cell sizes (x,y,z) of three ZnCdTe nanorod models considered in the present study are 10.6, 10.6 and 33.5 Å respectively. Cross section and side views of the initial structures of the three ZnCdTe nanorod models are shown in Figure 2.

Figure 1: Unit cells for the three nanorod models of Zn_xCd_1-xTe.

Figure 2: Side and cross section views of the generated structures of three ZnCdTe nanorod models.

Results and Discussions

In this section, the method of calculation described above has been applied to compute structural properties of Zn_xCd_1-xTe ternary alloys nanorods with Zn concentrations for x= 0.25, 0.50 and 0.75. CdTe and ZnTe have the cubic Zinc Sulfide, or Zinc Blende structure [40]. The Zn_xCd_1-xTe ternary alloys were obtained by means of a ZnTe crystal with Cd atoms substituted for a fraction x of the Zn atoms.

Figure 3 shows side and cross-section views with the corresponding total interaction energies of the Zn_0.25Cd_0.75Te nanorod at different temperatures. As can be seen from Figure 2, the structure of the Zn_0.25Cd_0.75Te nanorod changes depending on temperature. When the temperature reaches 900 K, the energy of the system begins to rise and after reaching 300 K, Zn atoms start to separate from the composition up until 1500 K, where they then disappear completely. The number of atoms remaining in terms of different temperatures for the three ZnCdTe nanorod models is given in Table 2. Figure 4 shows the number of Zn atoms variation with temperature for ZnCdTe nanorod models.

As temperature increases, a uniformly distributed Zn0.25Cd0.75Te nanorod becomes a more random distribution. The cross sections as well as the top view of the nanorods simulated are displayed in Figure 3. As seen in the figures the change from the nanorod structure to the tubular structure takes place as a result of increasing temperature.

Figure 3: The structures of Zn_0.25Cd_0.75Te nanorod at different temperatures. Pictures show side and cross-section views with the corresponding total interaction energies.

Figure 5 shows side and cross-section views with the corresponding total interaction energies of the Zn_0.50Cd_0.50Te nanorod at different temperatures. As can be seen from the figure the structure of the Zn_0.50Cd_0.50Te nanorod shows a dependence on temperature increase and stochiometry. When the temperature reaches 900 K, the energy of the system begins to rise. Zn atoms evaporate completely at a temperature of 1800 K and CdTe atoms remain and display a uniform structure. After reaching a temperature of 300 K, the nanorod starts to form a tubular structure as clearly seen from the cross section of the side view. In addition to this, Zn atoms show a tendency to separate from the nanorod with temperature increase like the other composition (Zn_0.25Cd_0.75Te). However, Zn0.25Cd0.75Te and Zn0.50Cd0.50Te nanorods have different structural characteristics than each other.

Side and cross-section views with the corresponding total interaction energies of the Zn_0.75Cd_0.25Te nanorod at different temperatures are displayed in Figure 6 for x=0.75. Zn atoms in this model decrease significantly from 72 atoms to 0 atoms when the temperature increases from 1 to 2100 K. After reaching a temperature of 1800 K, only Cd and Te atoms remain in the nanorod. Unlike the other compounds, a three-dimensional Zn_0.75Cd_0.25Te nanorod becomes a two-dimensional structure between 1200 K and 1800 K. Figure 6 clearly shows both sides and cross section views. It is interesting to note that after reaching 1800 K a 2D structure changes to become 3D in some sort of capsule like structure connected with an atom chain.

Figure 4: The number of Zn atoms variation with temperature for ZnCdTe nanorod models.

Figure 5: Same as Figure 2 but for Zn_0.50Cd_0.50Te.

Figure 6: Same as Figure 2 but for Zn_0.75Cd_0.25Te. Pictures for 1200, 1500 and 1800 K have two different side views.

Table 1: Potential parameters used in the calculations.

Table 2: Number of atoms in the ZnCdTe nanorod models at different temperatures. At 1 K there is no missing atom in all the models.

Conclusions

Classical molecular dynamics simulations using an atomistic many-body potential energy function (PEF) for Zn_xCd_1-xTe (x= 0.25, 0.50 and 0.75) nanorods have been performed. The calculations clearly showed that the Zn_xCd_1-xTe nanorods simulated at various temperatures and stoichiometry have different structural properties. After reaching a temperature of 300K, Zn_0.25Cd_0.75Te and Zn_0.50Cd_0.50Te nanorods change from a nanorod to a tubular structure as a result of temperature increases. On the other hand, the Zn0.75Cd0.25Te nanorod changes to become 2D (nanoribbon like structure) at 1200 K, it changes again to become 3D (capsule like structure) and a 1D (atom chain) structure at 2100 K. In all three nanorod structures, Zn atoms start to separate from the system after reaching 300 K. After Zn evaporation the total energy of the systems show an increasing trend as seen from the Figures 3, 5 and 6. We hope that the outcomes of the present study will provide useful information in understanding the structural properties of Zn_xCd_1-xTe (x= 0.25, 0.50 and 0.75) nanorods at various temperatures for both experimental and theoretical efforts.

References

1. KC Mandal, SH Kang, M Choi, J Bello, L Zheng H. Zhang M, et al. Simulation, Modeling, and Crystal Growth of Cd0.9Zn0.1Te for Nuclear Spectrometers. J Electron Mater. 1996;35:1251-1256.
2. KC Mandal, SH Kang, M Choi, J Wei, L Zheng, H Zhang, et al. Component Overpressure Growth and Characterization of High-Resistivity CdTe Crystals for Radiation Detectors. J Electron Mater. 2007;36: 1013-1020.
3. KC Mandal, SH Kang, M Choi, A Mertiri, C Noblitt, A Smirnov. Crystal Growth and Characterization of CdTe and Cd0.9Zn0.1Te for Nuclear Radiation Detectors. Proc Mat Res Soc Symp. 2008;1038:39-49.
4. UN Roy, A Gueorguiev, S Weiller, J Stein. Growth of spectroscopic grade Cd0.9Zn0.1Te: In by THM technique. J Cryst Growth. 2009;312:33-36.
5. Y Eisen, A Sho, I Mardor. CdTe and CdZnTe gamma ray detectors for medical and industrial imaging systems, Nucl. Instrum. Methods Phys Res A. 1999;428:158-170.
6. AA Melnikov. CdZnTe radiation detectors. J Cryst Growth. 1999;197:663-665.
7. A Gupta, V Parikh, AD Compaan. High efficiency ultra-thin sputtered CdTe solar cells. Sol Energ Mat Sol C. 2006;90:2263-2271.
8. T Gandhi, KS Raja, M Misra. Cadmium zinc telluride (CZT) nanowire sensors for detection of low energy gamma-ray detection. SPIE 6959 (2008), pp. 695904-1-13.
9. Y Wang, Y Hou, A Tang, B Feng, Y Li, J Liu, F Teng. Synthesis and optical properties of composition-tunable and water-soluble ZnxCd1-xTe alloyed nanocrystals. J Cryst Growth. 2007;308:19-25.
10. Y Wang, Y Hou, H Cui, C Sun, Y Lu. Controllable Synthesis and Electroluminescence Property of Water-Sol ZnCdTe Alloy for Light-emitting Diodes. IJAPM . 2011;1:167-170.
11. K Davami, J Pohl, M Shaygan, N Kheirabi, H Faryabi, I Cuniberti, JS Lee and M. Meyyappan, Bandgap engineering of CdxZn1-xTe nanowires. Nanoscale. 2013; 5:932-935.
12. S Li, Y Jiang, D Wu, L Wang, H Zhong, B Wu, X Lan, Y Yu, Z Wang and J Jie, Enhanced p-Type Conductivity of ZnTe Nanoribbons by Nitrogen Doping. J Phys Chem C. 2010;114:7980-7985.
13. K. Davami, D. Kang, J-S. Lee and M. Meyyappan, Synthesis of ZnTe nanostructures by vapor-liquid-solid technique. Chem Phys Lett. 2011;504: 62-66.14. T Gandhi, KS Raja and M Misra, Synthesis of ZnTe nanowires onto TiO2 nanotubular arrays by pulse-reverse Electrodeposition. Thin Solid Films. 2009;517:4527-4533.
14. H Faryabi, K Davami, N Kheirabi, M Shaygan, JS Lee and M Meyyappan Post-growth modification of electrical properties of ZnTe nanowires. Chem Phys Lett. 2013;543 :117-120.
15. X Wang, CS Ozkan. Multisegment Nanowire Sensors for the Detection of DNA Molecules. Nano Lett. 2008; 8:398-404.
16. HW Liang, S Liu, QS. Wu and SH Yu, An efficient templating approach for synthesis of highly uniform CdTe and PbTe nanowires. Inorg Chem. 2009; 48:4927-4933.
17. Z Hackney, L Mair, K Skinner and S Washburn. Photoconductive and polarization properties of individual CdTe nanowires. Mater Lett. 2010; 64: 2016-2018.
18. JE Lennard-Jones. Perturbation problems in quantum mechanics, Proc. Roy. Soc. London, Ser. A 129 (1930), pp. 598-615.
19. BM Axilrod and E Teller. Interaction of the Van der Waals type between three atoms. J Chem Phys. 1943; 11:299-300.
20. L Amirouche and S Erkoç. Structural features and energetics of ZnkCdl microclusters. J Mod Phys C. 2003;14: 905-910.
21. L Amirouche and S Erkoç. Structural features and energetics of Znn-mCdm (n=7,8) microclusters, and Zn50, Cd50 and Zn25Cd25 nanoparticles: Molecular-dynamics simulations. Phys Rev A. 2008;8:043203-1-6.
22. L Amirouche and S Erkoç, Molecular-dynamics simulations of surface and bulk properties of Zn, Cd, and ZnCd systems. Phys Stat Sol. 2004;(b)241:292-297.
23. E Pearson, T Takai, T Halicioglu, WA Tiller. Computer modeling of Si and SiC surfaces and surface processes relevant to crystal growth from the vapor. J Cryst Growth. 1984;70:33-40.
24. DK. Choi, T Takai, S Erkoç, T Halicioglu, WA Tiller. Free Surfaces and Multilayer Interfaces in the GaAs/AlAs System. J Cryst Growth. 1987;85:9-15.
25. DK Choi, MS Koch, T Takai, T Halicioglu, WA Tiller. Simulation of GaAs cluster formation on GaAs(001), AIAs(001), Si(001), and As1/Si(001) surfaces. J Vac Sci Technol. 1988;B 6:1140-1144.
26. S Erkoç, T Halicioglu, WA Tiller. Adsorption of Gold Adatoms on GaAs (110) Surface: A Molecular Dynamics Simulation. Phys Stat Sol 1989;(b)156:K105-K107.
27. T Takai. Computer Simulation of Silicon, Carbon, Silicon Carbide and Gold: Surface Processes and Energetics [Ph.D. Thesis]. Stanford University; 1984.
28. C Lee. Configurations of Small Si/O Clusters. Phys Stat Sol. 1987 ;(b)139: K93-K97.
29. H Oymak, S Erkoç. Structural and electronic properties of AlkTilNim microclusters: Density functional theory calculations. Phys Rev. 2002; A 66 : 33202-1-10.
30. S Erkoç, H Oymak. AlTiNi ternary alloy clusters: molecular-dynamics simulations and density-functional-theory calculations. J Phys Chem. 2003;B 107: 12118-12125.
31. A Ince, S Erkoç. Silicene nanoribbons: Molecular-dynamics simulations. Mater Chem Phys. 2011; 50: 865-870.
32. B Ozdamar, S Erkoç. Structural properties of silicon nanorods under strain: Molecular dynamics simulations. J Comput Theor Nanos. 2013; 10:1-9.
33. S Kr Bhattacharya, A Kshirsagar. Ab initio calculations of the structural and electronic properties of CdTe clusters. Phys Rev. 2007;B 75: 35402 -1-10.
34. KP Huber, G Herzberg. Molecular Spectra and Molecular Structures: Constants of Diatomic Molecules: Van Nostrand Reinhold Co., New York; 1979.
35. O Babaky and K Hussein, Molecular constants of 128Te2. Can J Phys. 1991;69:57-61.
36. A Nordsieck. On Numerical Integration of Ordinary Differential Equations. Math Comput. 1962; 16: 22-49.
37. CW Gear, Numerical Initial Value Problems in Ordinary Differential Equations: Prentice-Hall, EnglewoodCliffs,NJ;1971.
38. DJ Evans, GP Morris, Non-Newtonian molecular Dynamics. Comp Phys Rep. 1984;1:297-243.
39. J Steiniger, AJ Strauss, RF Brebrick. Phase Diagram of the Zn-Cd-Te Ternary System. J Electrochem Soc. 1970;117:1305-1309.