ISSN: 2322-0066
ISSN: 2322-0066
Mathematics/Physics teacher at Ngao girls, Secondary School, Kenya
Received Date: 20/06/2017; Accepted Date: 29/06/2017; Published Date: 21/06/2017
Visit for more related articles at Research & Reviews: Research Journal of Biology
I presented a method of solving the Bring-Jerrard quintic equation by converting it to a solvable factorized form. That is, I seek to present a factorized form into which the Bring-Jerrard quintic equation can be reduced. In so doing, I show that the Bring-Jerrard quintic equation is reducible. This means that the Bring-Jerrard quintic equation can be solved in terms lower degree polynomials. The Bring-Jerrard quintic is the trinomial form of the quintic equation. By presenting a reducible form of the BringJerrard quintic I also demonstrate that the quintic equation is in general reducible to solvable lower degree polynomials.
Bring-Jerrard quintic equation, Algebra, Factorial design, Polynomials
Quintic equations are part of polynomial equations. Polynomial equations have many real world applications. The aim of this contribution is to further contribute to understanding of methods of solving quintic equations.
The general quintic equation takes the form 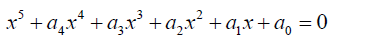 0.1
0.1
From literature (e.g. Cajori [1] and Struik [2]) polynomial equations were first investigated more than four thousand years ago.
The general quintic equation takes the form 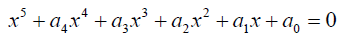 0.1
0.1
Abel and Ruffini showed that proved that it impossible to solve over a field of rational numbers, see Rosen [3]
Bring [4] and Jerrard [5] have shown that the equation can be reduced to a simple form with two parameters. That is, x5 + px + q = 0=0 0.2
The equation 0.2 above is now called the Bring-Jerrard quintic equation.
Glashan [6], Young [7], Runge [8] showed that some form of the Bring-Jerrard quintic equation is solvable in radicals. Spearman and William [9] came with similar results.
Many others contributed in various ways:
Motlotle [10], in his master’s thesis managed to present a formula for solving the Bring-Jerrard quintic equation using the Newton’s sum formula. In his contribution Motlotle convincingly argued that Abel’s impossibility proof has been misconstrued by many as meaning that no general algebraic solution of the quintic equation is attainable. He showed that such a formula in unattainable only within a field of Rational numbers. He then moved on to deriving a formula.
In this contribution I present a solvable factorized form to which the Bring- Jerrard quintic equation can be converted to make it solvable. That is I will seek to reduce the Bring-Jerrard quintic equation to quadratic and cubic factors. To achieve a general solution will seek to establish a functional relationship between the parameters of the lower degree auxiliary factors and those of the Bring-Jerrard quintic equation.
Consider the Bring-Jerrard quintic equation:
x5 + px + q = 0 0.1
Factorized form selected:
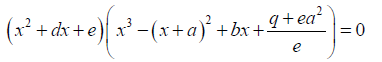 0.2
0.2
The form selected above is similar to that used by Buya SB [11] in his attempt to present a method to solve the general quintic equation.
If in the expansion of 0.2:
1) The x4 coefficient equated to zero then
d=1 0.3
2) The x3coefficient is equated to zero and substituting 0.3 into the resulting equation:
e=2a-b + 1 0.4
3) The x2 coefficient is equated to zero and substituting 0.3 then we obtain the equation:
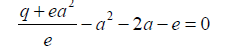 0.5
0.5
0.5 can be simplified to:
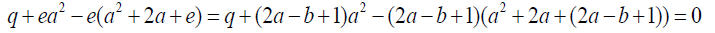 0.6
0.6
Equation 0.6 further simplifies to:
q - (2a-b+1) (4a-b+1)=0 0.7
4) Equating the x coefficient to p and simplifying:
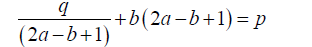 0.8
0.8
Let:
2a-b+1=u 0.9
4a-b+1=v 1.0
From 0.8:
q=uv 1.1
From 0.9 and 1.0:
b=2 u- v + 1 1.2
Substituting 0.9, 1.0, 1.1 and 1.2 into 0.8 and simplifying:
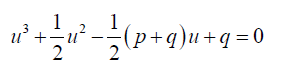 1.3
1.3
If we let 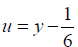 1.4
1.4
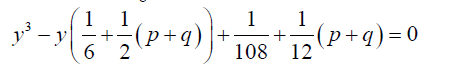 1.5
1.5
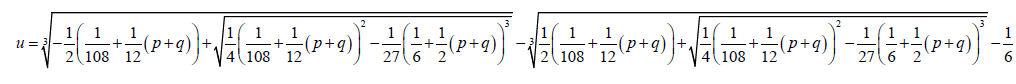 1.6
1.6
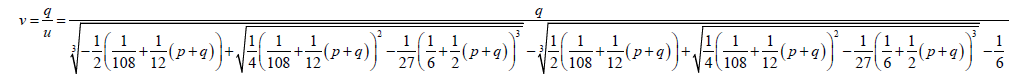 1.7
1.7
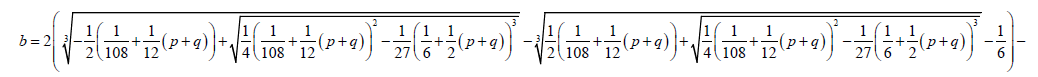
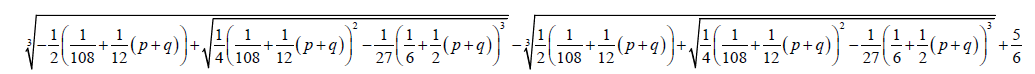 1.8
1.8
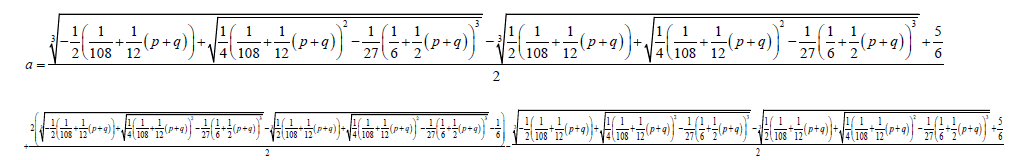 1.9
1.9
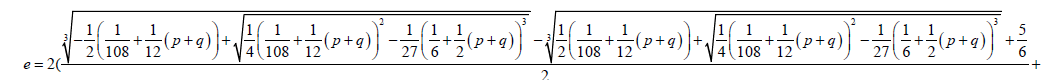
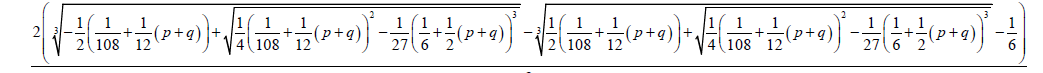
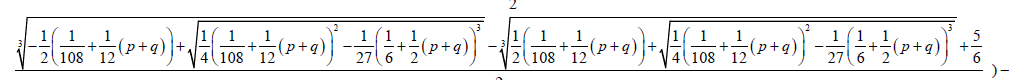
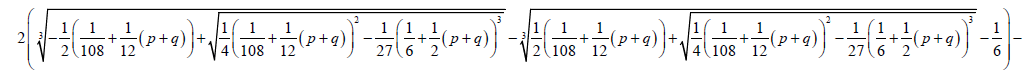
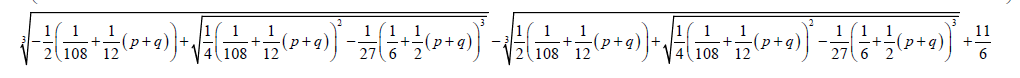
The Factorized form 0.2 of the Bring-Jerrard quintic equation is solved by substitution of the above coefficients in the auxiliary cubic and quadratic equations.
Two of the roots of the Bring-Jerrard quintic equations are;
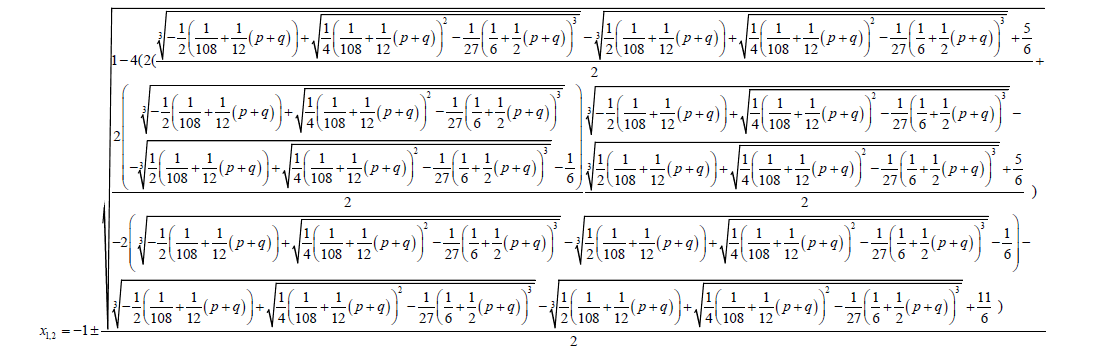
The other three roots of the quintic equation can be found by solving the auxiliary cubic equation:
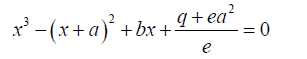 2.1
2.1
The Bring-Jerrard quintic equation (and the Quintic equation in general) is reducible to cubic and quadratic factors. A formula has been achieved for solving the quintic equation in terms of the lower degree polynomials to which it has been reduced. Quintic equations can in general be solved algebraically. The Galois group associated with the quintic equation is solvable over algebraic numbers.